Multi-Mean Gaussian Processes: A novel probabilistic framework for multi-correlated functional data

Abstract

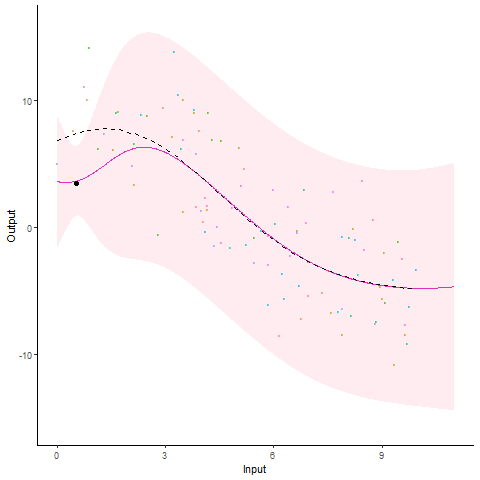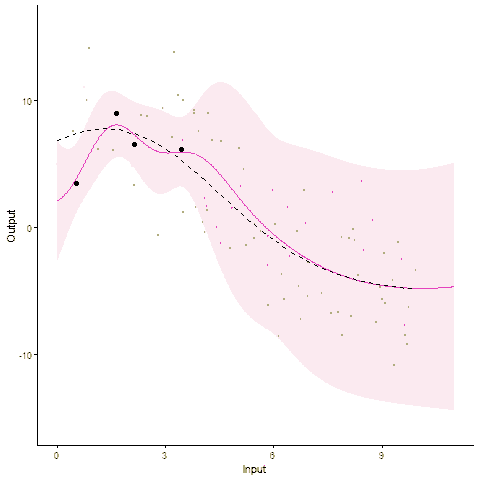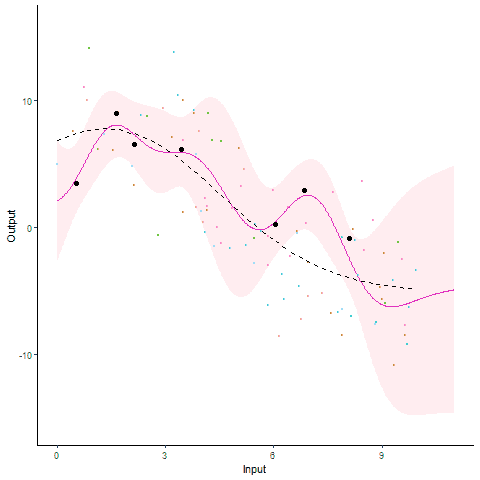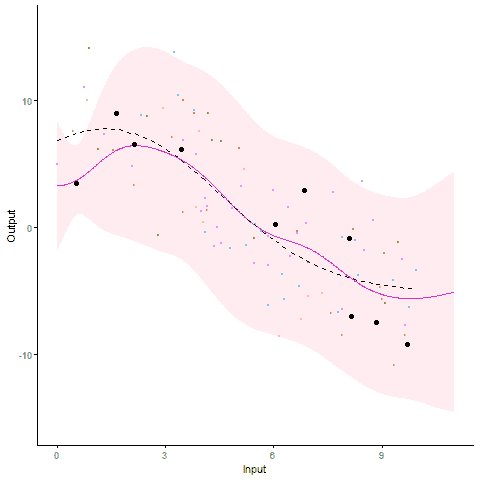
Modelling and forecasting time series, even with a probabilistic flavour, is a common and well-handled problem nowadays. In particular, Gaussian processes are by essence tailored to represent continuous phenomena, and several approaches have been proposed during the past decades to handle multiple tasks in one model. From the original definition of coregionalisation kernels, many approaches have been explored, with the constraint that the number of tasks remain reasonable (the complexity generally scales cubically with the number of tasks). However, suppose now that one is collecting data from hundreds of individuals, each of them gathering thousands of gene-related measurements, all evolving continuously over time. Such a context, frequently arising in biological or medical studies, quickly leads to highly correlated datasets where dependencies come from different sources (temporal trend, gene or individual similarities for instance). Explicit modelling of overly large covariance matrices accounting for these underlying correlations is generally unreachable due to theoretical and computational limitations. Therefore, practitioners often need to restrict their analysis by working on subsets of data or making arguable assumptions (fixing time, studying genes or individuals independently, …). Recently, a novel paradigm for defining multi-task Gaussian processes models has been proposed and tailored to handle multiple time series simultaneously. In this approach, a latent mean process common to all tasks is introduced, and knowledge is transferred through hyper-posterior computations and subsequent marginalisation. In this paper, we aim at offering an overview of this framework, and propose a more general formulation allowing us to handle multiple sources of correlations.