Multi-Mean Gaussian Processes: A novel probabilistic framework for
multi-correlated longitudinal data
Arthur Leroy - Department of Computer
Science, The University of Manchester
joint work with
- Mauricio Alvarez - Department
of Computer Science, The University of Manchester
- Dennis Wang - Department of
Computer Science, The University of Sheffield
- Ai Ling Teh - Singapore
Institute for Clinical Sciences
NeurIPS Workshop on Gaussian Processes, Spatiotemporal
Modeling, and Decision-making Systems - 02/12/2022
Longitudinal data observed from multiple irregular sources
Gaussian processes offers an elegant
and well-suited framework for modelling longitudinal data.
Until then, most multi-task approaches focus on the covariance
structure. Let us present a novel multi-task GP paradigm sharing
information through a common mean
process.
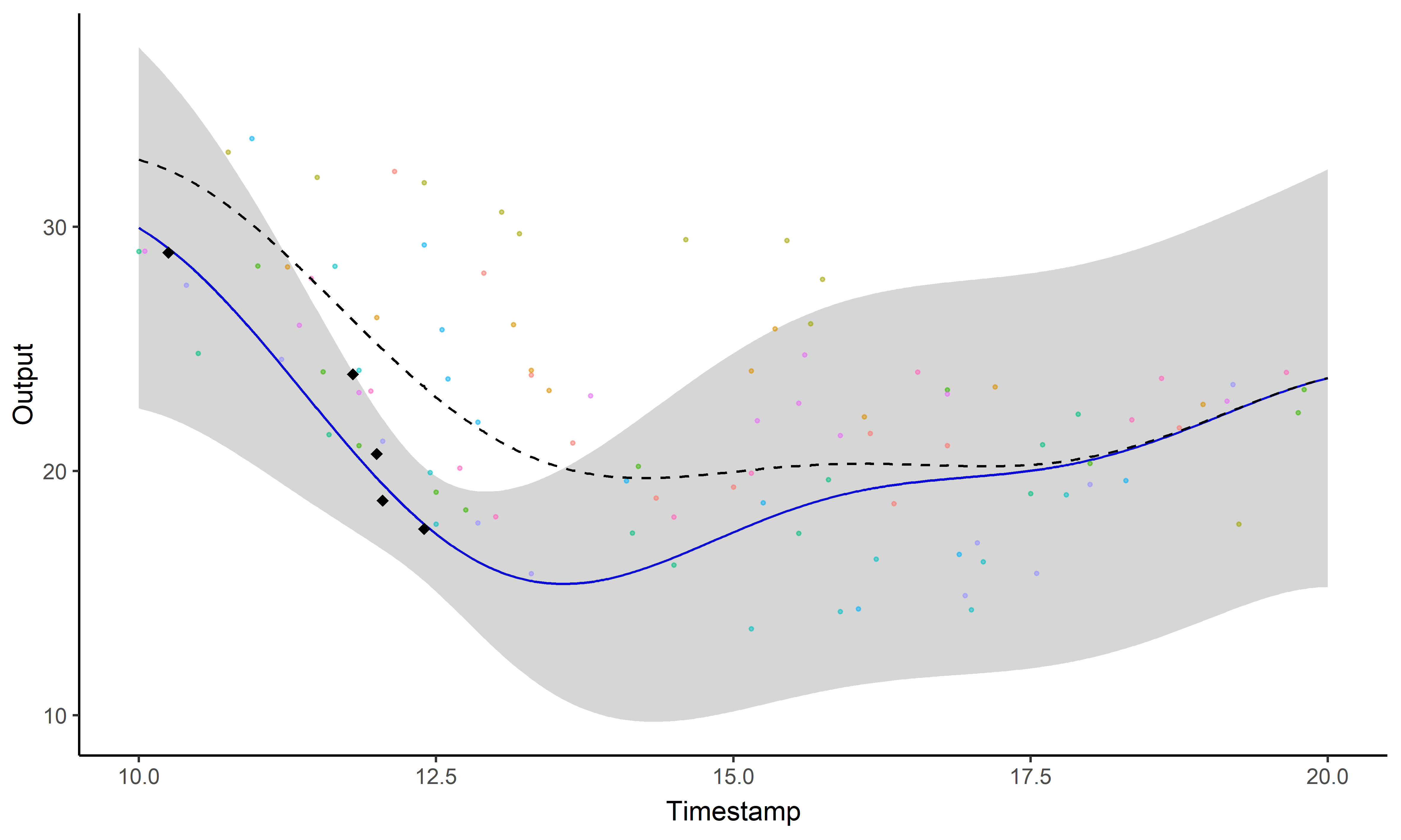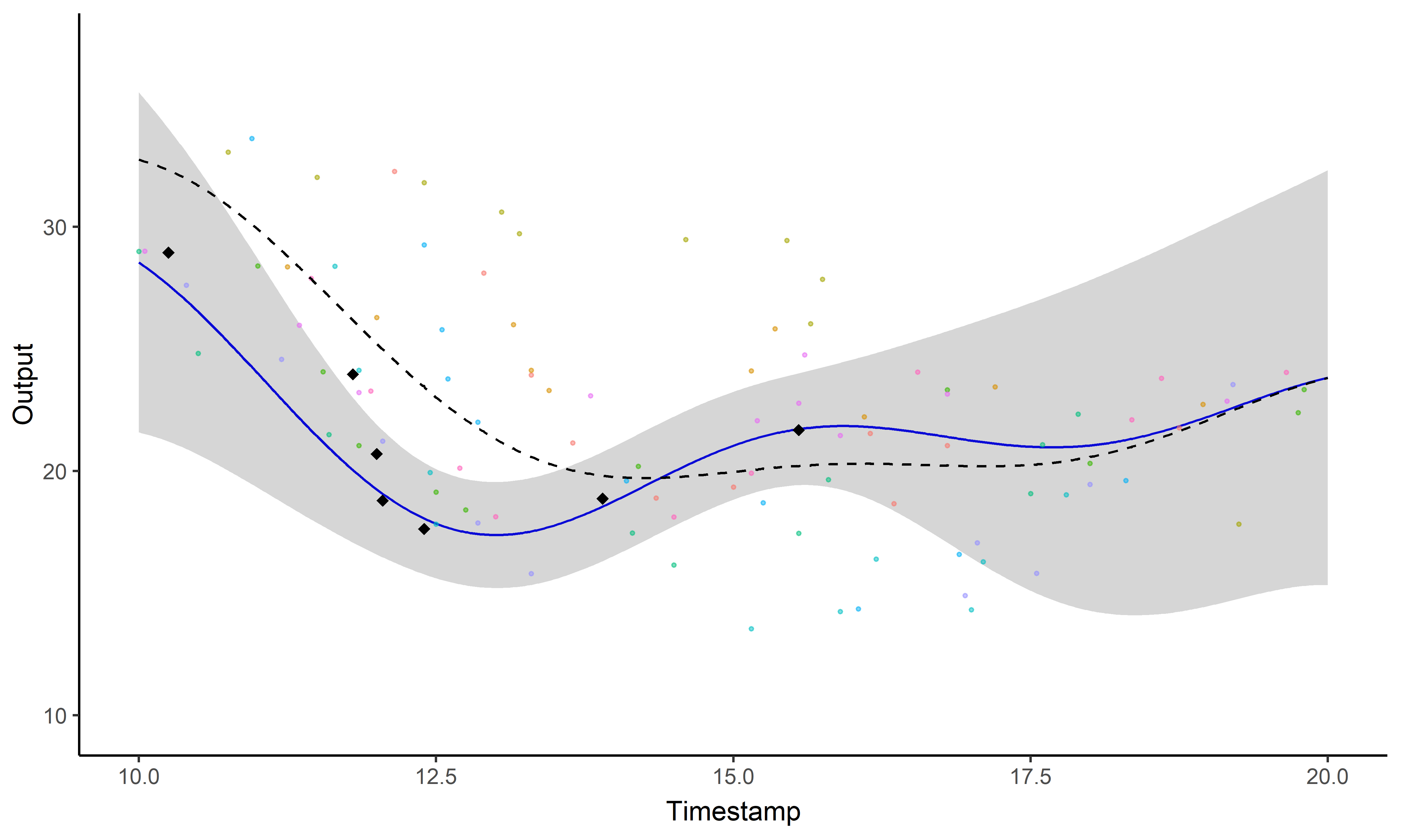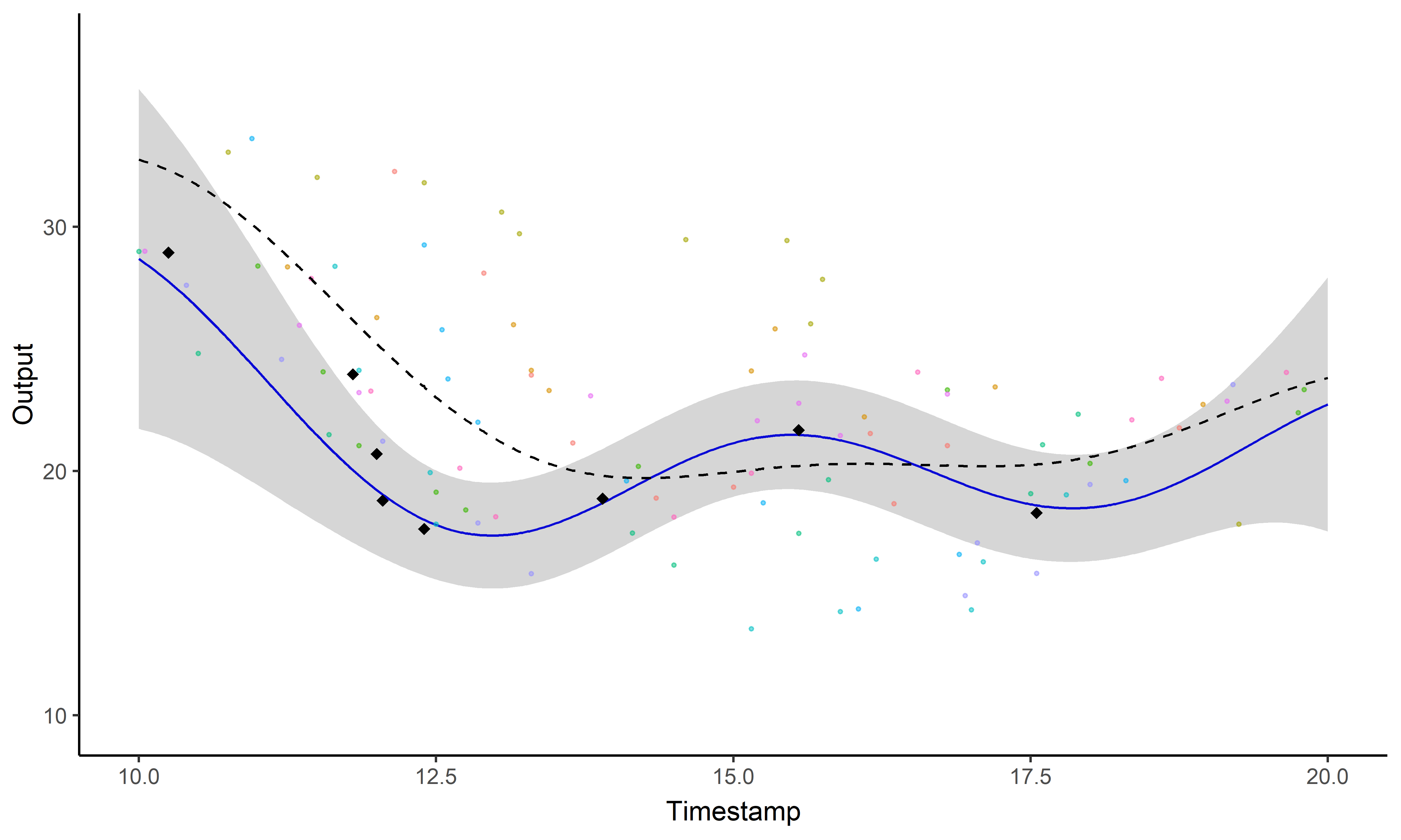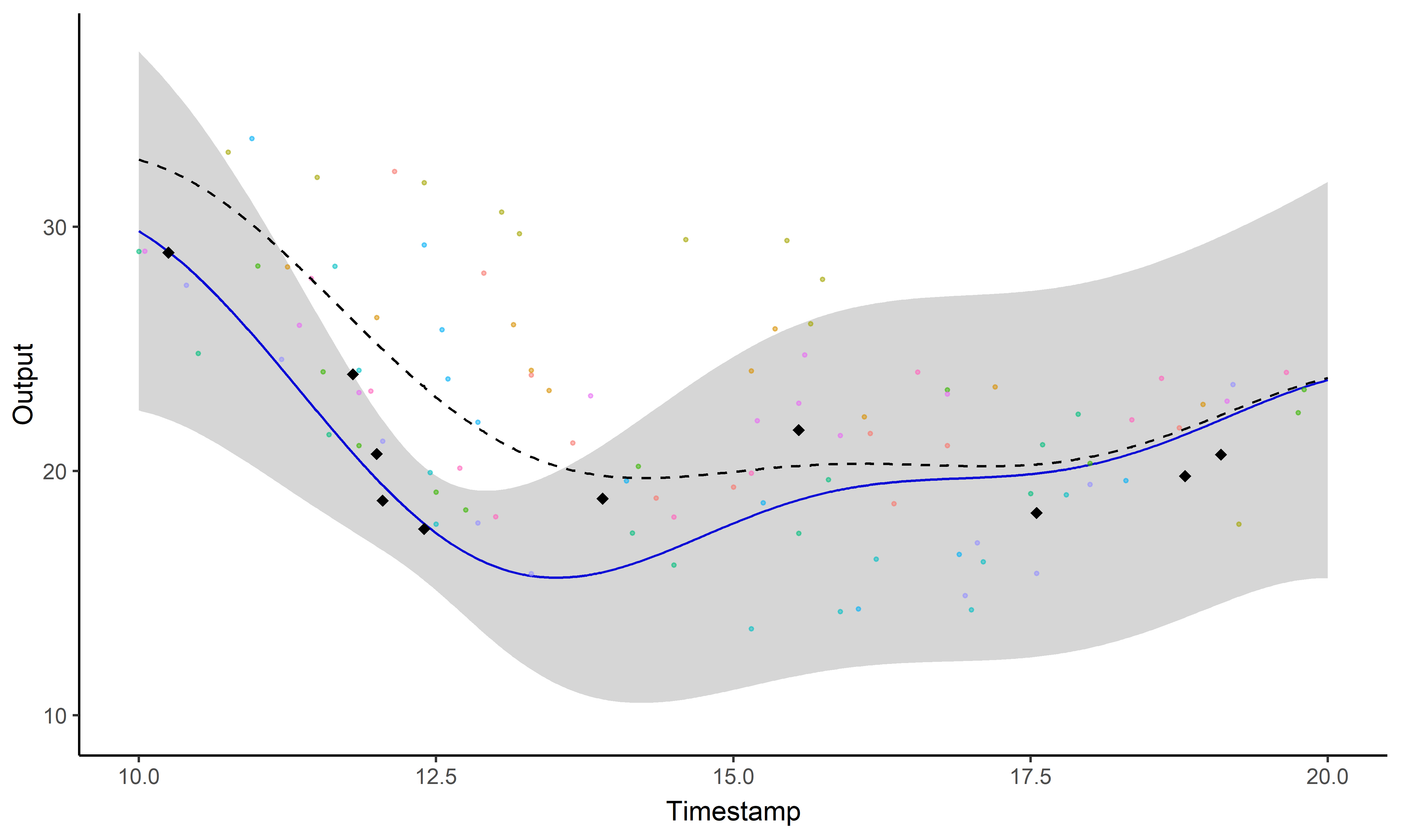
Leroy et al. - Magma: Inference and Prediction using
Multi-Task Gaussian Processes with Common Mean - Machine Learning -
2022
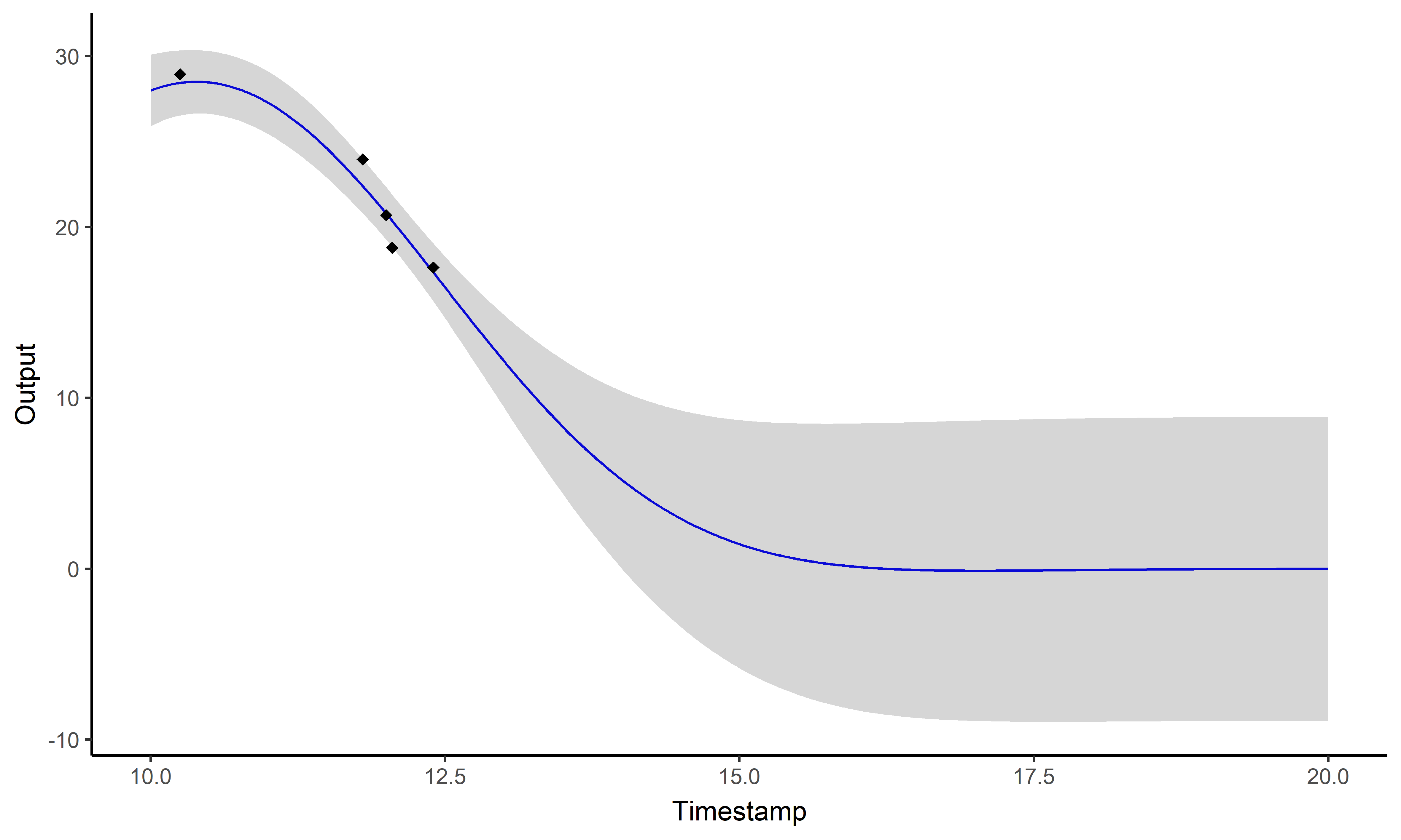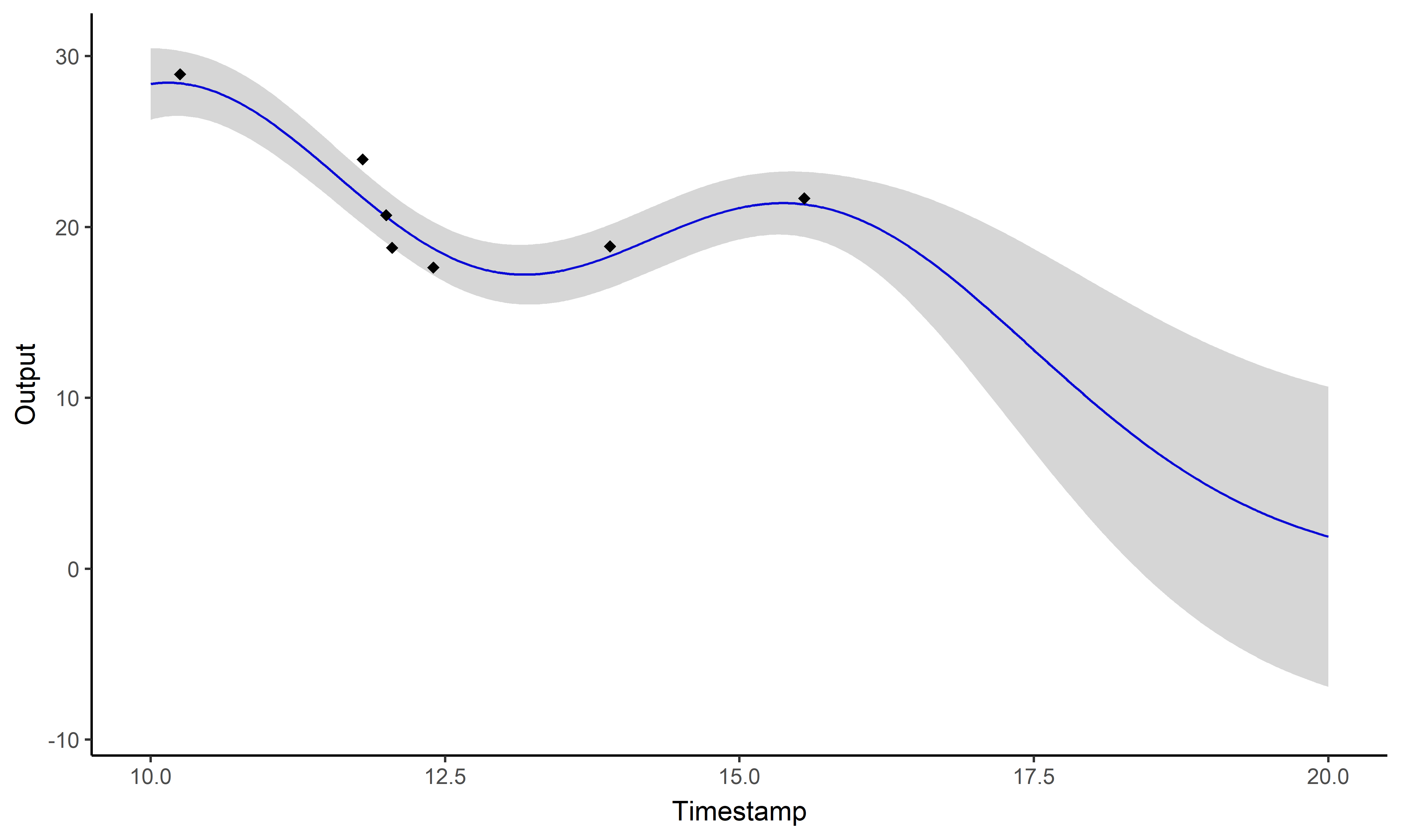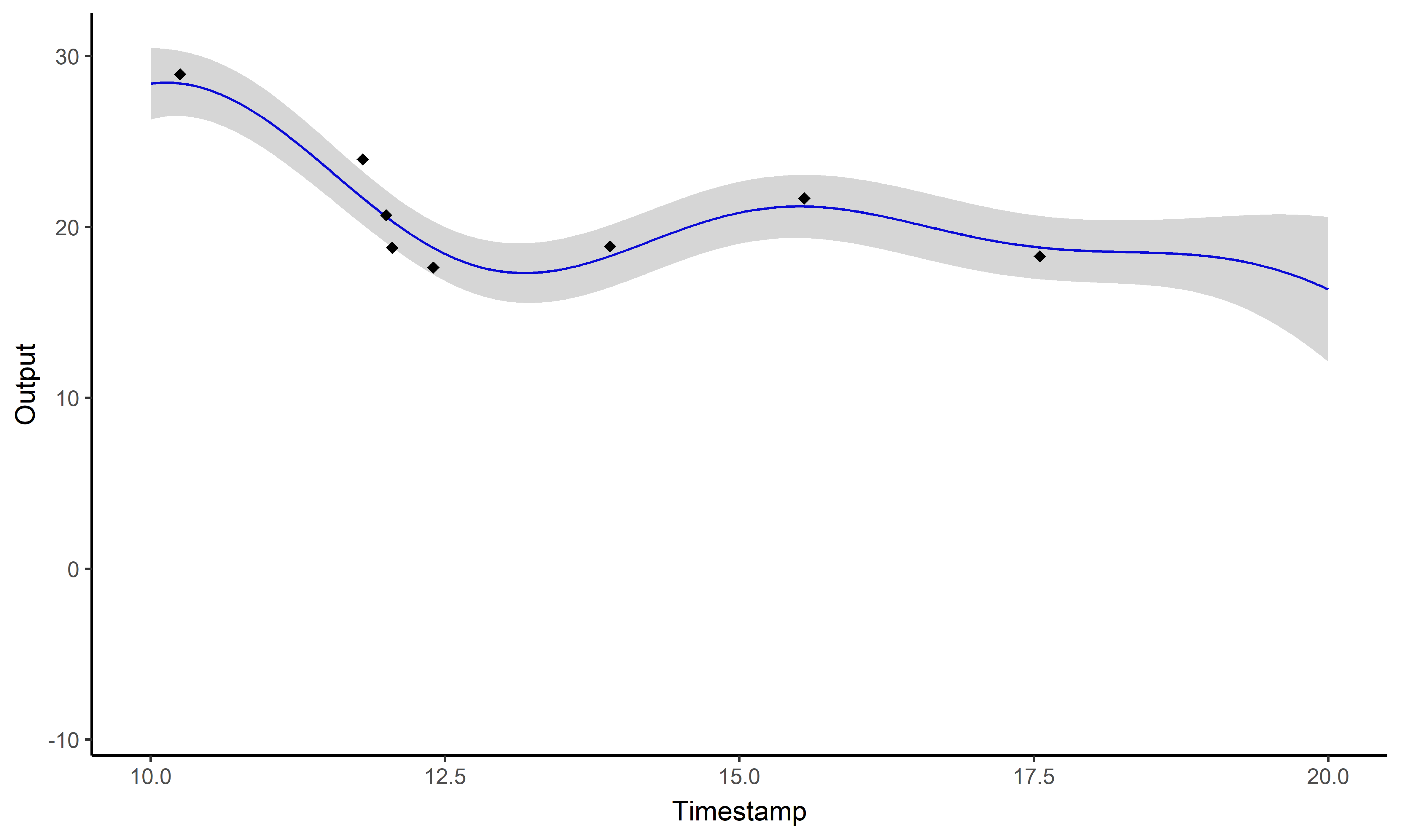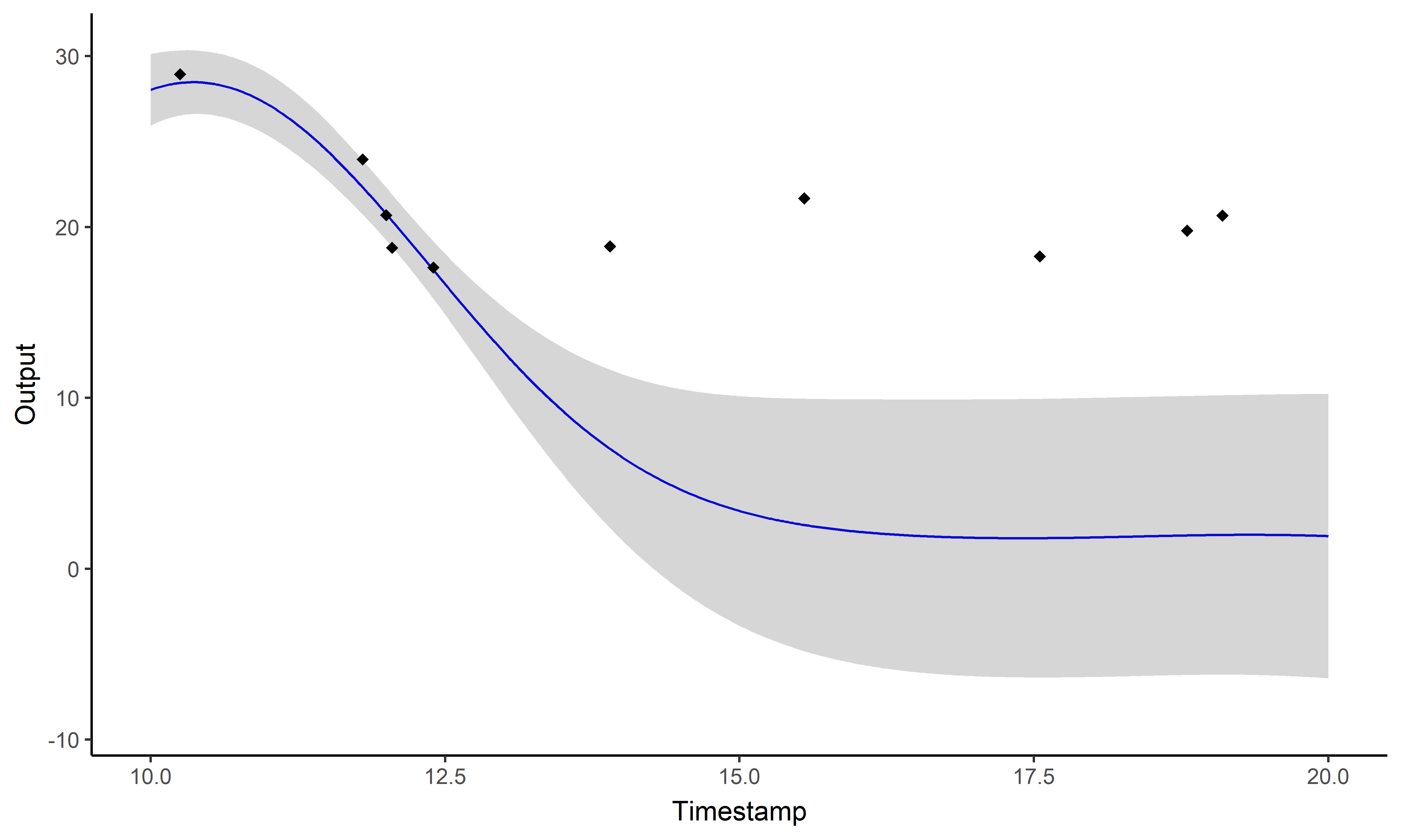
\[y_i = \mu_0 + f_i +
\epsilon_i\]
with: \(\ \ \ \mu_0 \sim
\mathcal{GP}(m_0, K_{\theta_0}), \ \ \ f_i \sim \mathcal{GP}(0,
\Sigma_{\theta_i}), \ \ \ \epsilon_i \sim \mathcal{GP}(0,
\sigma_i^2)\)
Leroy et al. - Cluster-Specific Predictions with
Multi-Task Gaussian Processes - Accepted in JMLR - 2022
\[y_i \mid \{\color{orange}{Z_{ik}} = 1 \}
= \mu_{\color{orange}{k}} + f_i + \epsilon_i\]
with: \(\ \ \ \color{orange}{Z_{i}}
\sim \mathcal{M}(1,\color{orange}{\boldsymbol{\pi}}), \ \ \
\mu_{\color{orange}{k}} \sim \mathcal{GP}(m_{\color{orange}{k}},
\color{orange}{C_{\gamma_{k}}}), \ \ \ f_i \sim \mathcal{GP}(0,
\Sigma_{\theta_i}), \ \ \ \epsilon_i \sim \mathcal{GP}(0,
\sigma_i^2).\)
![]()
![]()
Multi-Mean Gaussian processes framework
\[y_{\color{blue}{i}\color{red}{j}} =
\mu_{0} + f_\color{blue}{i} + g_\color{red}{j} +
\epsilon_{\color{blue}{i}\color{red}{j}}\]
Key idea: compute multiple dedicated
posterior mean processes
\[p(\mu_0 \mid
\{y_{\color{blue}{i}\color{red}{j}} \}_{\color{blue}{i} = 1,\dots,
\color{blue}{M}}) = \mathcal{N}\Big(\mu_{0}; \
\hat{m}_{\color{red}{j}}, \hat{K}_\color{red}{j} \Big), \ \forall
\color{red}{j} \in 1, \dots, \color{red}{P}\] \[p(\mu_0 \mid \{y_{\color{blue}{i}\color{red}{j}}
\}_{\color{red}{j} = 1,\dots, \color{red}{P}})
= \mathcal{N}\Big(\mu_{0}; \
\hat{m}_{\color{blue}{i}}, \hat{K}_\color{blue}{i} \Big), \forall
\color{blue}{i} \in 1, \dots, \color{blue}{M} \]
![]()
![]()
Multi-Mean Gaussian Processes: A novel probabilistic framework for
multi-correlated longitudinal data
Arthur Leroy - Department of Computer
Science, The University of Manchester
joint work with
- Mauricio Alvarez - Department
of Computer Science, The University of Manchester
- Dennis Wang - Department of
Computer Science, The University of Sheffield
- Ai Ling Teh - Singapore
Institute for Clinical Sciences
NeurIPS Workshop on Gaussian Processes, Spatiotemporal
Modeling, and Decision-making Systems - 02/12/2022
