Classification automatique :
Méthodes et mise en application

Arthur Leroy - Université de Paris

DU Dataviz - 7 et 8 Avril 2021

Coordonnées et références

Arthur Leroy :
- arthur.leroy.pro@gmail.com
- https://arthur-leroy.netlify.app/
Références (liste non-exhaustive) :
- Analyse de Données avec R, F. Husson, S. Lê, J. Pagès, Presses Universitaires de Rennes.
- Statistique Exploratoire Multidimensionnelle, L. Lebart, M. Piron, A. Morineau, DUNOD.
- Package R FactoMineR : http://factominer.free.fr/
- MOOC Analyse des Données Multidimensionnelles, F. Husson, sur plateforme FUN.

Planning de la journée

Introduction
- Données et exemples de visualisation
- Classification automatique
Méthodes et mise en oeuvre
- Classification Ascendante Hiérarchique
- Centres mobiles
- Classification sur facteurs

Introduction

Table de données brutes

satisf = read.csv2("Donnees/Villes.csv", header = T)
x = satisf[,-1]
rownames(x) = satisf$ville
head(x)

##            accessibilite dynamisme.economique emploi taille cadre.de.vie
## Lille               18.3                 10.4   12.5   15.8         10.3
## douai-lens          14.5                 13.2    8.2   12.4          9.9
## lyon                14.4                 12.9   18.5   20.0          8.3
## rouen               14.0                 10.8   12.7   17.6         11.0
## nantes              13.9                 16.5   17.9   15.0         11.2
## rennes              13.2                 14.9   17.9   18.2         10.1
##            culture immobilier meteo offre.de.soins securite
## Lille         18.9        2.4   4.7            6.6      3.0
## douai-lens    10.1       14.6   4.7            2.0      5.4
## lyon          19.8        3.2  14.7           10.1      2.6
## rouen         16.6        5.2   1.7            9.4      5.7
## nantes        16.6        5.9   7.6            9.8      9.8
## rennes        17.1        5.4   6.8           17.8     14.9

Visualisation des données sur le premier plan factoriel

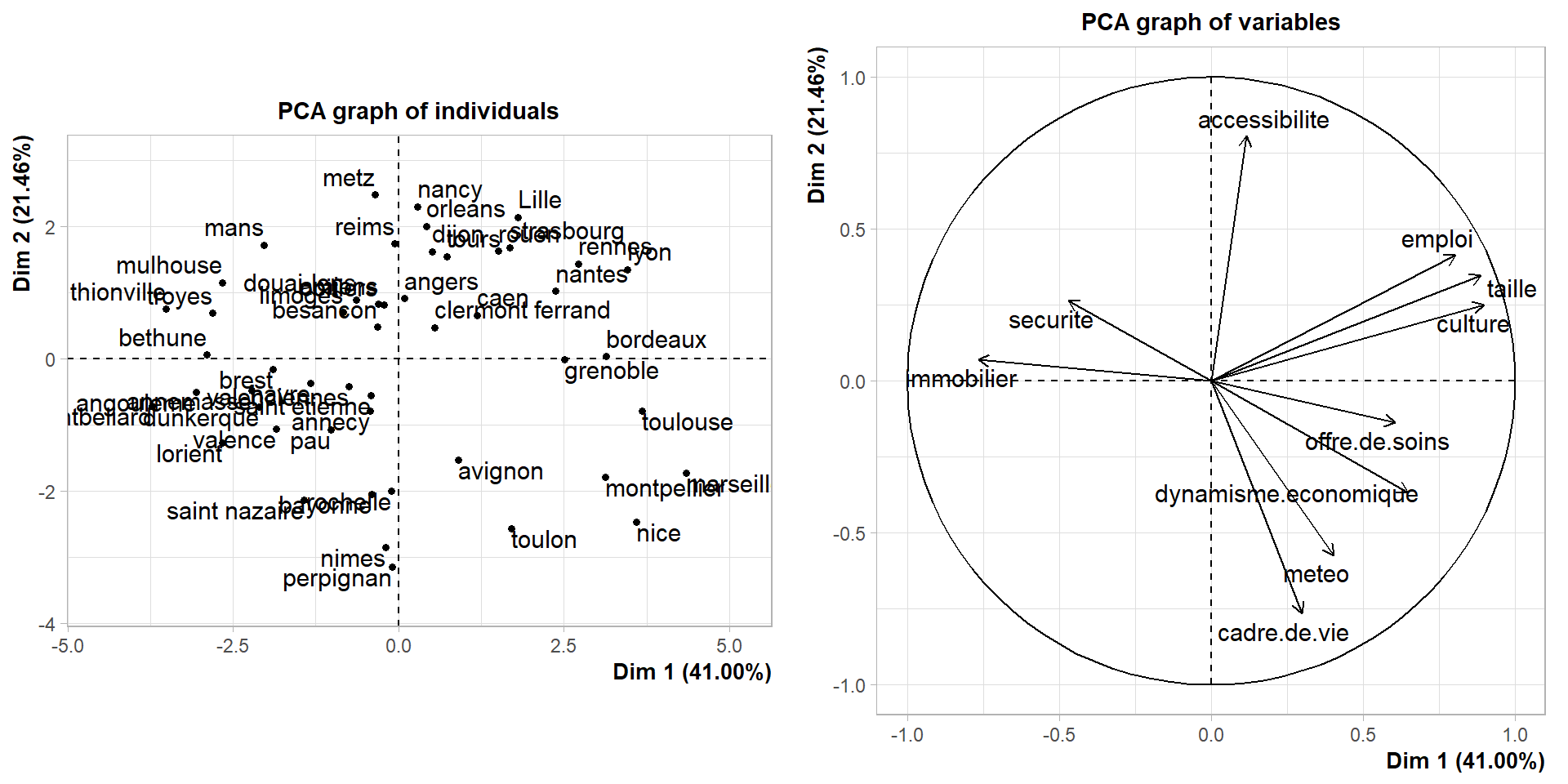
Visualisation des groupes sur le premier plan factoriel

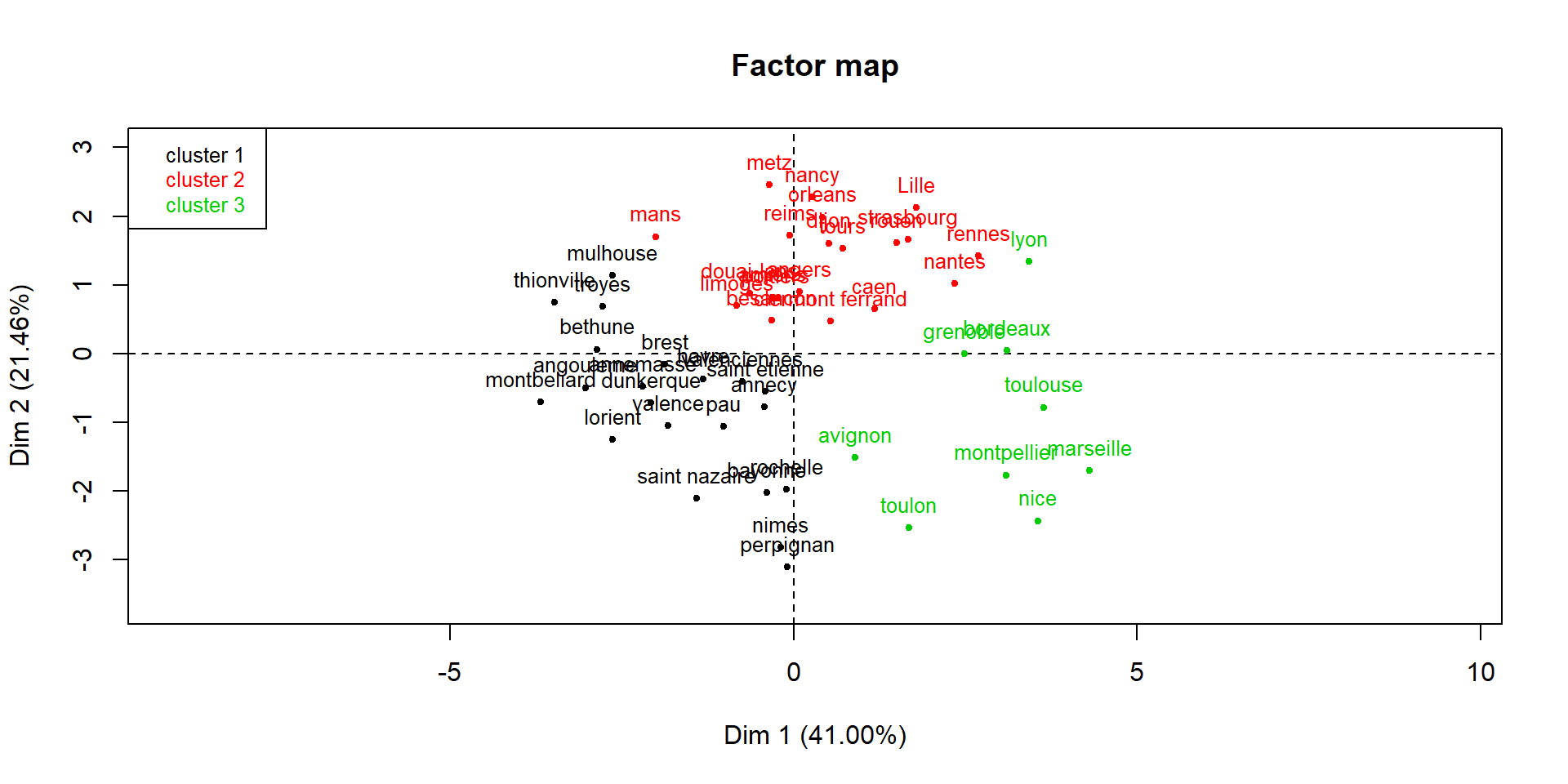
Classification automatique

Objectifs : à partir d’une table de données contenant $n$ individus et $p$ variables quantitatives,
- regrouper les individus en $k$ groupes, avec $k<n$, de telle sorte que
  - les individus d’un même groupe soient les plus ressemblants possibles,
  - les individus appartenant à des groupes différents soient les plus dissemblables possibles,
  - un individu appartient à un et un seul groupe.
- Caractériser les groupes.
Mise en oeuvre : algorithmes d’approximation (solution optimale inatteignable en termes de complexité de calcul).
Contraintes : les groupes, ainsi que leur nombre $k$, sont en général inconnus.

Méthodes de classification automatique

Classification ascendante hiérarchique (CAH) :
- regroupement des individus, puis des groupes, deux à deux, de manière à former une hiérarchie de groupes,
- choix d’un nombre de groupes,
- caractérisation de la classification obtenue.
Centres mobiles :
- choix de $k$ fixé a priori,
- formation de $k$ groupes rassemblant les individus les plus proches de $k$ centres fixés a priori,
- mise à jour des centres par les points moyens à l’intérieur de chaque groupe,
- itération jusqu’à convergence vers une classification stable.

Méthodes et Mise en Oeuvre

Classification Ascendante Hiérarchique

Hiérarchie de parties : ensemble de groupes ``emboîtés’’.
Cette représentation traduit la façon dont ils sont construits :
- soit par réunion successive de parties (ascendante),
- soit par division successive (descendante).
La relation d’inclusion conduit à une représentation graphique du type :

Représentation graphique

Ordre de formation : traduction des différents niveaux de ressemblance entre les groupes.
Ordre utilisé pour ordonner le graphique suivant l’axe vertical :

Représentation graphique (2)

Indice de diamètre : indice numérique quantifiant la variabilité entre les groupes

$\Longrightarrow$ hiérarchie indicée.
Représentation graphique = dendrogramme.

CAH : l’algorithme de base

Etape 1:
- Calcul des distances entre chaque élément de l’échantillon de données.
- Regroupement des 2 individus les plus proches $\Rightarrow$ obtention de $n-1$ groupes.
- L’indice de diamètre des parties à 1 individu est $0$, et celui de la partie obtenue par fusion des 2 individus est proportionnel à la distance entre ces 2 individus.
Etape j ($1\leqslant j\leqslant n-1$) :
- Calcul des dissemblances entre chaque partie obtenue à l’étape $j-1$.
- Regroupement des deux parties les plus proches $\Rightarrow$ obtention de $n-j$ groupes.
- L’indice de diamètre du nouveau groupe obtenu est proportionnel à la dissemblance entre les 2 groupes dont il est issu.
Fin de l’algorithme : A l’étape $n-1$, lorsque tous les individus sont regroupés dans un seul groupe.

Agrégation de groupes

Agrégation des groupes : choix d’une dissemblance $\delta$ permettant de quantifier la différence entre les groupes. $\delta$ repose elle-même sur le choix d’une distance $d$ entre les points, en général $d =$ distance euclidienne : pour $p=2$

Si $x = (x^{(1)};\ldots;x^{(p)})$ et $y = (y^{(1)};\ldots;y^{(p)})$, alors \[d(x,y) = \sqrt{\sum_{j=1}^p\left(x^{(j)}-y^{(j)}\right)^2}\]

Dissemblance : les choix

Dissemblances : Exemples
- saut minimal (lien simple) : \[\delta_{min}(A,B)=\mbox{min}\{d(x,y) \ ; \ x\in A, \ y\in B\}\]
- saut maximal (lien complet) : \[\delta_{max}(A,B)=\mbox{max}\{d(x,y) \ ; \ x\in A, \ y\in B\}\]
- saut moyen (lien moyen) : \[\delta_{moy}(A,B)=\frac{\sum_{\{ x\in A, \ y\in B\}}d(x,y)}{card(A)\times card(B)}\]

Dissemblance : les choix (2)

Exemple pour $\delta_{min}$ et $\delta_{max}$

Critère de Ward

Critère nécessitant l’utilisation de la distance euclidienne

$d$ distance entre 2 points = distance euclidienne.
Les groupes sont représentés par leur point moyen (ou centre de gravité).
La fusion de 2 groupes est représentée par le remplacement des 2 représentants de chaque groupe par le centre de gravité des 2 points, muni de la somme des masses.
Dans ce cadre, on ne regarde plus les distances pour choisir les groupes à fusionner, mais la décomposition de l’inertie (ou variance) selon les groupes d’une classification.

Décomposition de l’inertie (LMP)

Variance totale $=$ Variance inter-groupes $+$ Variance Intra-groupes

Qualité d’une classification (LMP)

Qualité de la classification en 2 groupes suivant la variance intra-groupes

Algorithme d’agrégation par critère de Ward

Principe général : Au depart de l’algorithme, l’inertie inter-classes est maximale ($n$ classes). A la fin, celle-ci est nulle (1 classe).

$\Rightarrow$ On minimise à chaque étape la perte d’inertie inter-classes (ou on maximise le gain d’inertie intra-classe).

A chaque étape: On regroupe les 2 groupes pour lesquels la perte d’inertie inter-classes est minimale.

Cela revient à regrouper les groupes $j$ et $j'$ (représentés par leurs centres $G_j$ et $G_j'$) pour lesquels la perte \[\Delta_{jj'}=\frac{n_jn_{j'}}{n_j+n_{j'}}d^2(G_j,G_{j'})\] est minimale.

Un exemple simple

Carrés des distances euclidiennes

Regroupement 1 et 3 $\Rightarrow$ nouvel individu 6

Un exemple simple (2)

Carrés des distances euclidiennes pondérés (arrondis)

Regroupement 2 et 5 $\Rightarrow$ nouvel individu 7

Un exemple simple (3)

Carrés des distances euclidiennes pondérés (arrondis)

Regroupement 4 et 6 $\Rightarrow$ nouvel individu 8

Un exemple simple (4)

Choix du nombre de groupes

Coupure du dendrogramme à un niveau donné de l’indice $\Longrightarrow$ classification.
La coupure doit se faire :
- après les agrégations correspondant à des valeurs peu élevées de l’indice,
- avant les agrégations correpondant à des niveaux élevés de l’indice (dissocient les groupes bien distincts dans la population).
Règle empirique : sélection d’une coupure lors d’un saut important de l’indice par inspection visuelle du dendrogramme.
Ce saut traduit le passage brutal entre des groupes d’une certaine homogénéité de l’ensemble à des classes beaucoup moins homogènes.
Dans la plupart des cas, il y a plusieurs paliers et donc plusieurs choix de classifications possibles.

Choix du nombre de groupes : exemple

Création des profils d’individus

Profils : profils créés à partir
- des représentants de chaque groupe constituant la classification,
- de la visualisation des groupes sur les plans factoriels, avec le cercle des corrélations.
Représentant : individu moyen du groupe, dont les mesures sur chaque variable sont les mesures moyennes calculées dans le groupe.
Analyse des profils à partir
- de l’analyse des représentants de chaque groupe,
- de la visualisation sur les plans factoriels.

La CAH sous R : exemple des Iris de Fisher

Les longueurs et largeurs de sépales et de pétales sont mesurées sur 150 iris, dont on connaît l’espèce : “setosa”, “versicolor” ou “virginica”.

str(iris)

## 'data.frame':    150 obs. of  5 variables:
##  $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
##  $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
##  $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
##  $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

La CAH sous R (2)

ACP sur les variables quantitatives :

library(FactoMineR)
iris.pca = PCA(iris, ncp = 4,
               quali.sup = 5, graph = FALSE)

Options de la fonction PCA :
- ncp : indique le nombre de composantes principales à calculer. Ici, autant qu’il y a de variables quantitatives (4). Par défaut, ncp = 5.
- quali.sup : projette le centre de gravité des modalités des variables qualitatives indiquées sur le plan factoriel. Ici, la variable qualitative est Species, en $5$ème position dans la table.
- quanti.sup : projette les variables quantitatives indiquées sur le plan factoriel.
- Les variables indiquées dans xxx.sup sont illustratives et ne participent pas à la construction des axes factoriels.
- graph : affiche ou non les projections des données et variables sur le premier plan factoriel. Par défaut, graph = TRUE.

La CAH sous R (3)

Représentation graphique sur le premier plan factoriel:

library(gridExtra) # pour afficher les graphiques
                   # côte à côte
p1 = plot(iris.pca, choix = "ind", label = "quali")
p2 = plot(iris.pca, choix = "var")
grid.arrange(p1,p2, ncol = 2, widths = c(7,7))

choix = “ind” : représentation des individus sur le plan factoriel,
choix = “var” : représentation du cercle des corrélations sur le plan factoriel,
axes = c(1,2) (défaut) : choix des axes représentés sur le plan factoriel,
label = “quali” : ajout des noms des modalités illustratives.
grid.arrange crée une grille (tableau) telle que 1 case = 1 graphique : ncol, nrow nombre de lignes et de colonnes de la grille. Ici 1 ligne et 2 colonnes. widths, heigths réglage des tailles des graphiques.

La CAH sous R (4)

Résultat du code précédent :

library(gridExtra) # pour afficher les graphiques
                   # côte à côte
p1 = plot(iris.pca, choix = "ind", label = "quali")
p2 = plot(iris.pca, choix = "var")
grid.arrange(p1,p2, ncol = 2)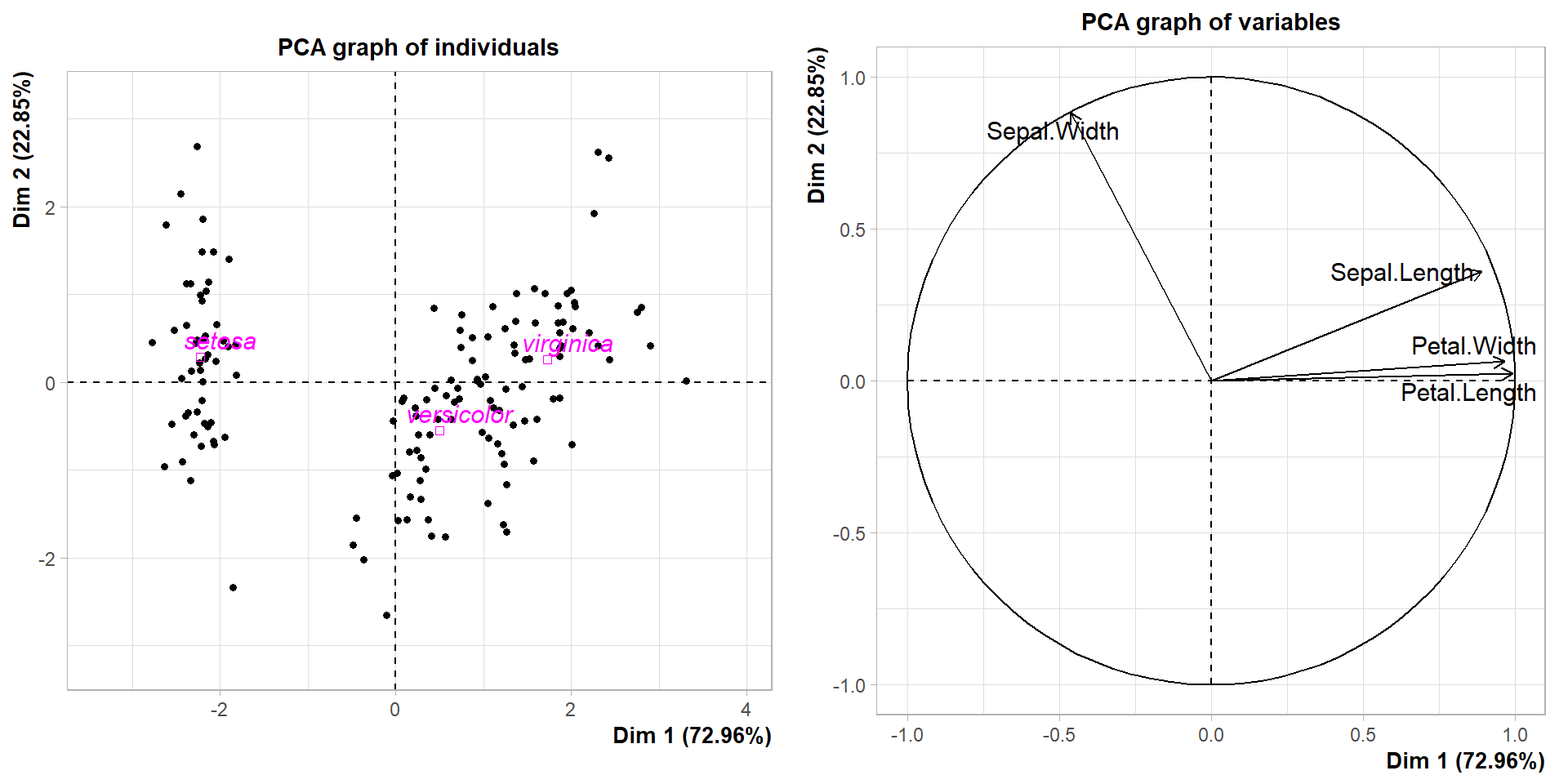

La CAH sous R (5)

summary(iris)

##   Sepal.Length    Sepal.Width     Petal.Length    Petal.Width   
##  Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100  
##  1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300  
##  Median :5.800   Median :3.000   Median :4.350   Median :1.300  
##  Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199  
##  3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800  
##  Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500  
##        Species  
##  setosa    :50  
##  versicolor:50  
##  virginica :50  
##                 
##                 
##

La CAH sous R (6)

Certaines variables sont sur une échelle jusqu’à $2$ fois plus grande que d’autres $\Longrightarrow$ avant de lancer la classification, nécessité de standardiser les variables afin d’éviter les problèmes d’échelle (sinon toute la classification s’appuiera sur la ou les variable(s) de plus grande échelle) :

iris.std = data.frame(scale(iris[,-5])) # ici, on enlève 
                                        # la variable
                                        # numéro 5, 
                                        # qui est 
                                        # qualitative

où la fonction data.frame permet de transformer l’objet rendu par scale en un format gérable en entrée par la fonction de classification.

Note : on peut calculer la matrice des dissemblances entre les individus de la base de données

D = dist(iris.std)

La CAH sous R (7)

Calcul du dendrogramme avec la fonction HCPC (librairie FactoMineR) :

dendro.ward = HCPC(iris.std, nb.clust = -1, 
                   consol = FALSE, method = "ward", 
                   graph = FALSE)

nb.clust : nombre de groupes souhaité. Si nb.clust = -1, un algorithme d’optimisation est utilisé pour le choisir automatiquement. Si nb.clust = 0 (par défaut), l’utilisateur choisit en cliquant sur le dendrogramme.
consol : applique ou non un algorithme de consolidation à l’aide des centres mobiles (voir suite du cours). Par défaut, consol = TRUE.
method : méthode d’agrégation des groupes. Les méthodes vues précédemment sont ward (méthode de Ward), single (lien simple), complete (lien complet) et average (lien moyen). Par défaut, method = ward.

La CAH sous R (8)

Représentation du dendrogramme :

plot(dendro.ward, choice = "tree", rect = FALSE)

choice = “tree” renvoie la représentation graphique du dendrogramme,
rect = FALSE ne représente pas les rectangles identifiant la classification. Par défaut rect = TRUE.
Le diagramme en barres représente l’inertie (= indice) nécessaire pour regrouper les groupes 2 à 2 au long de l’algorithme. Plus la différence d’inertie est grande, et plus les groupes rassemblés sont différents. Option tree.barplot = TRUE par défaut dans la fonction plot, mettre à FALSE pour ne pas le représenter.

La CAH sous R (9)

Résultat du code précédent :

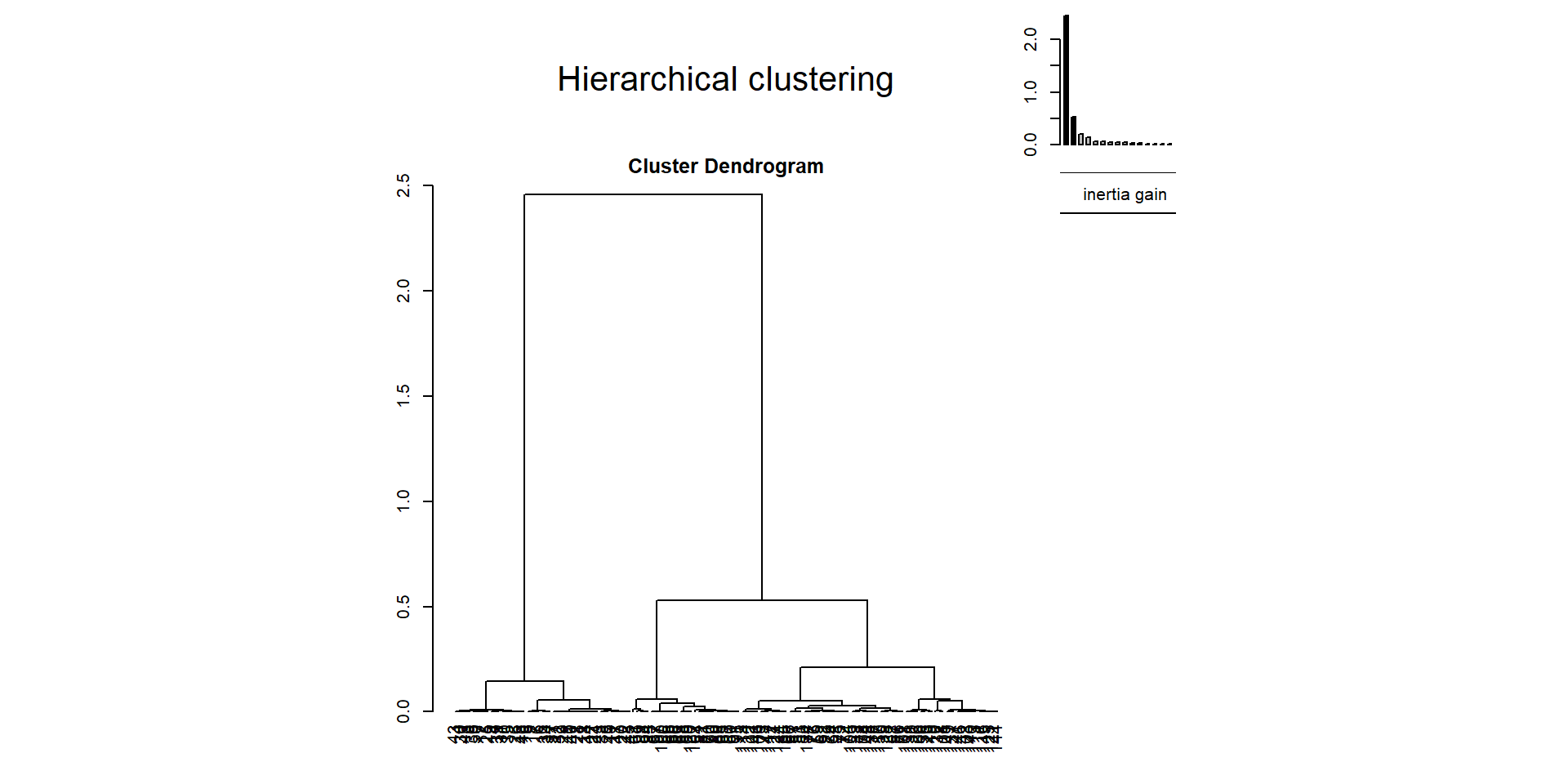
plot(dendro.ward, choice = "tree", rect = FALSE)

La CAH sous R (10)

Représentation du dendrogramme avec la classification choisie :

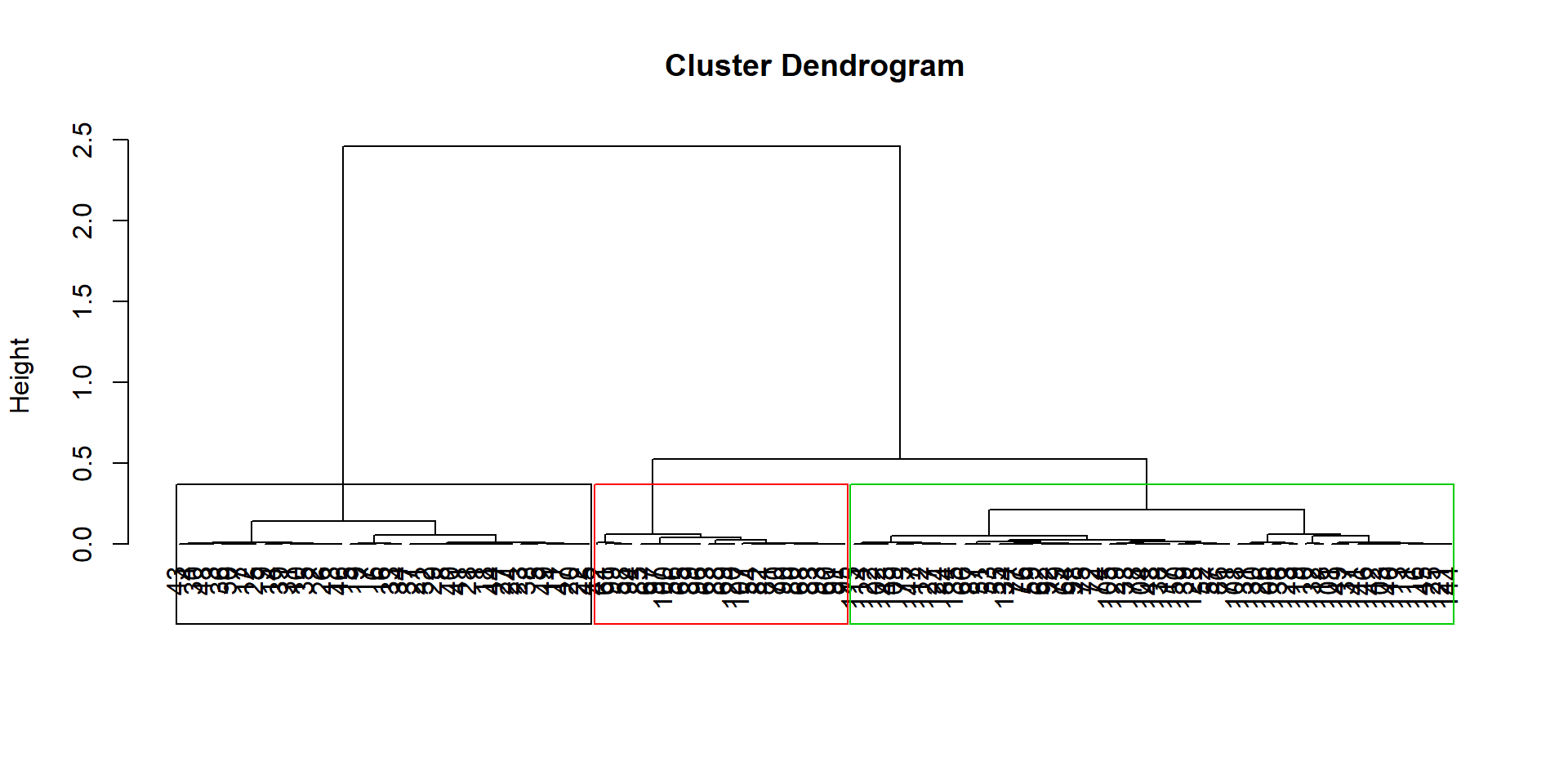
plot(dendro.ward, choice = "tree", tree.barplot = FALSE)

La CAH sous R (11)

Représentation des découpes possibles sur le dendrogramme

dendro.ward2 = HCPC(iris.std, nb.clust = 2, 
                   consol = FALSE, method = "ward", 
                   graph = FALSE)
par(mfrow=c(1,2)) # découpe la fenêtre graphique en 
                  # 2 cases (1 ligne, 2 colonnes)
plot(dendro.ward, choice = "tree", tree.barplot = FALSE)
plot(dendro.ward2, choice = "tree", tree.barplot = FALSE)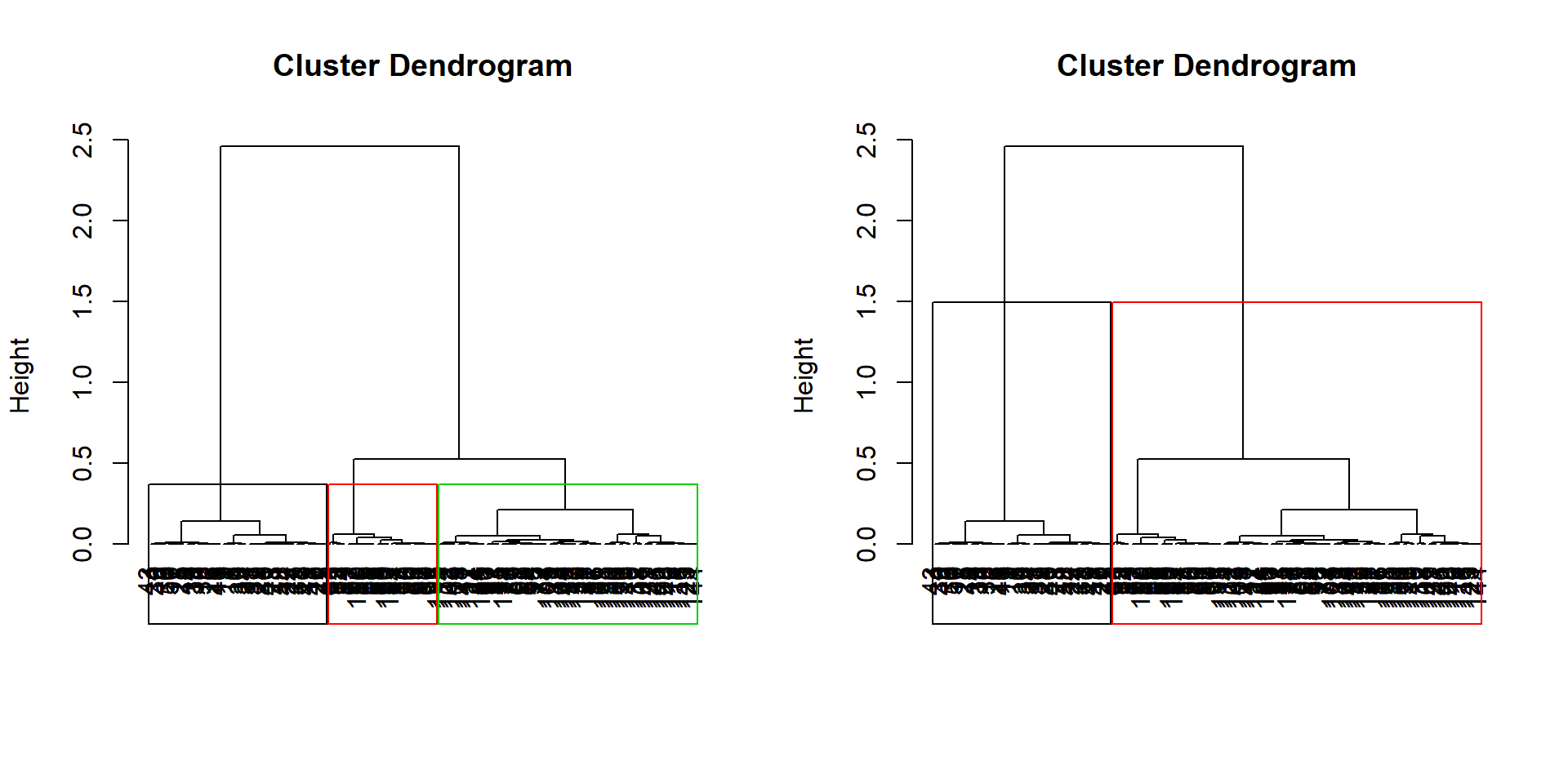

La CAH sous R (12)

Enlever les noms des observations en bas du dendrogramme :

par(mfrow=c(1,2))
plot(dendro.ward, choice = "tree", tree.barplot = FALSE,
     labels = FALSE)
plot(dendro.ward2, choice = "tree", tree.barplot = FALSE,
     labels = FALSE)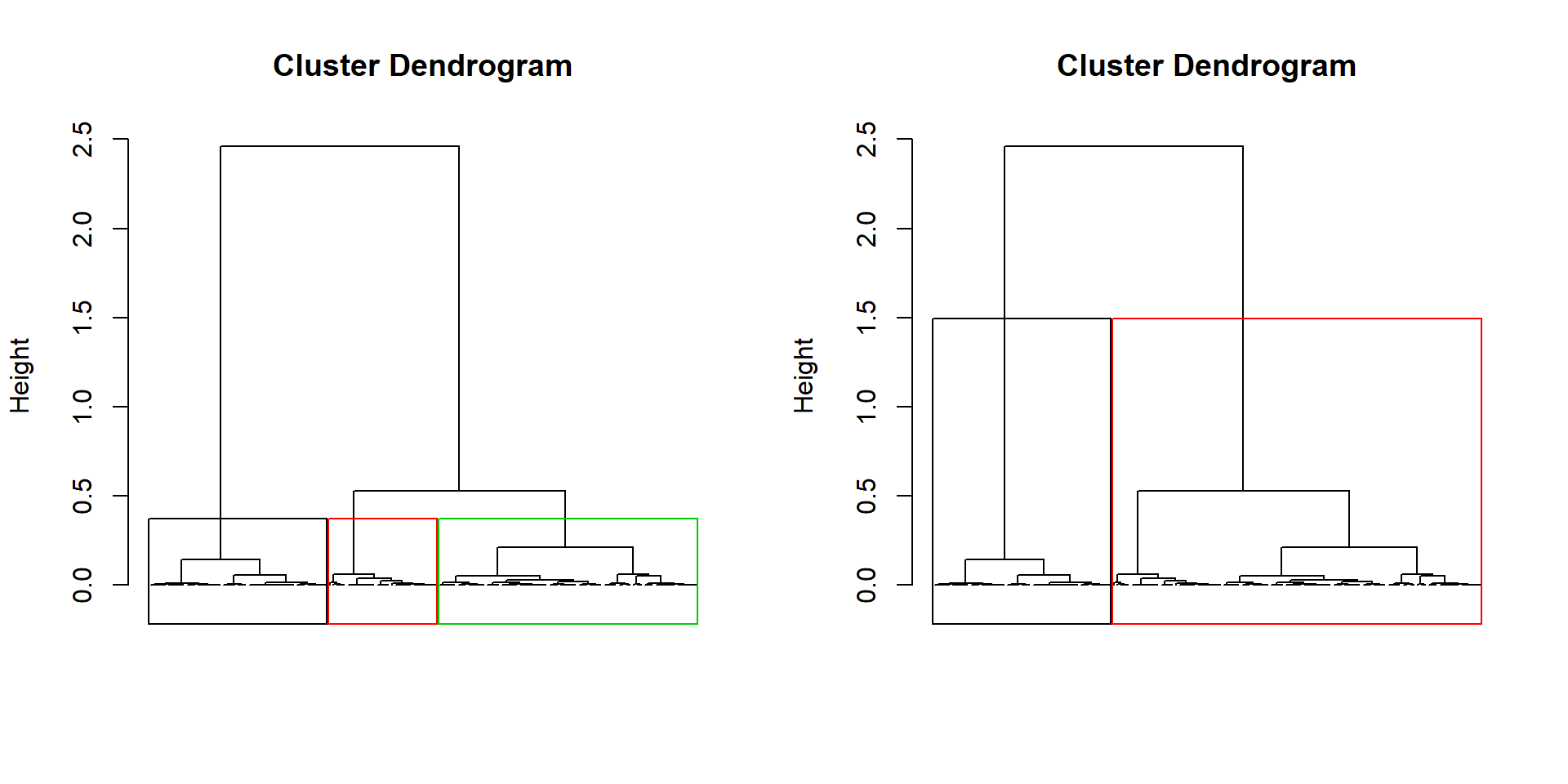

La CAH sous R (13)

Changer les titres des figures :

par(mfrow=c(1,2))
plot(dendro.ward, choice = "tree", tree.barplot = FALSE,
     main = "Classification à 3 groupes", labels = FALSE)
plot(dendro.ward2, choice = "tree", tree.barplot = FALSE,
     main = "Classification à 2 groupes", labels = FALSE)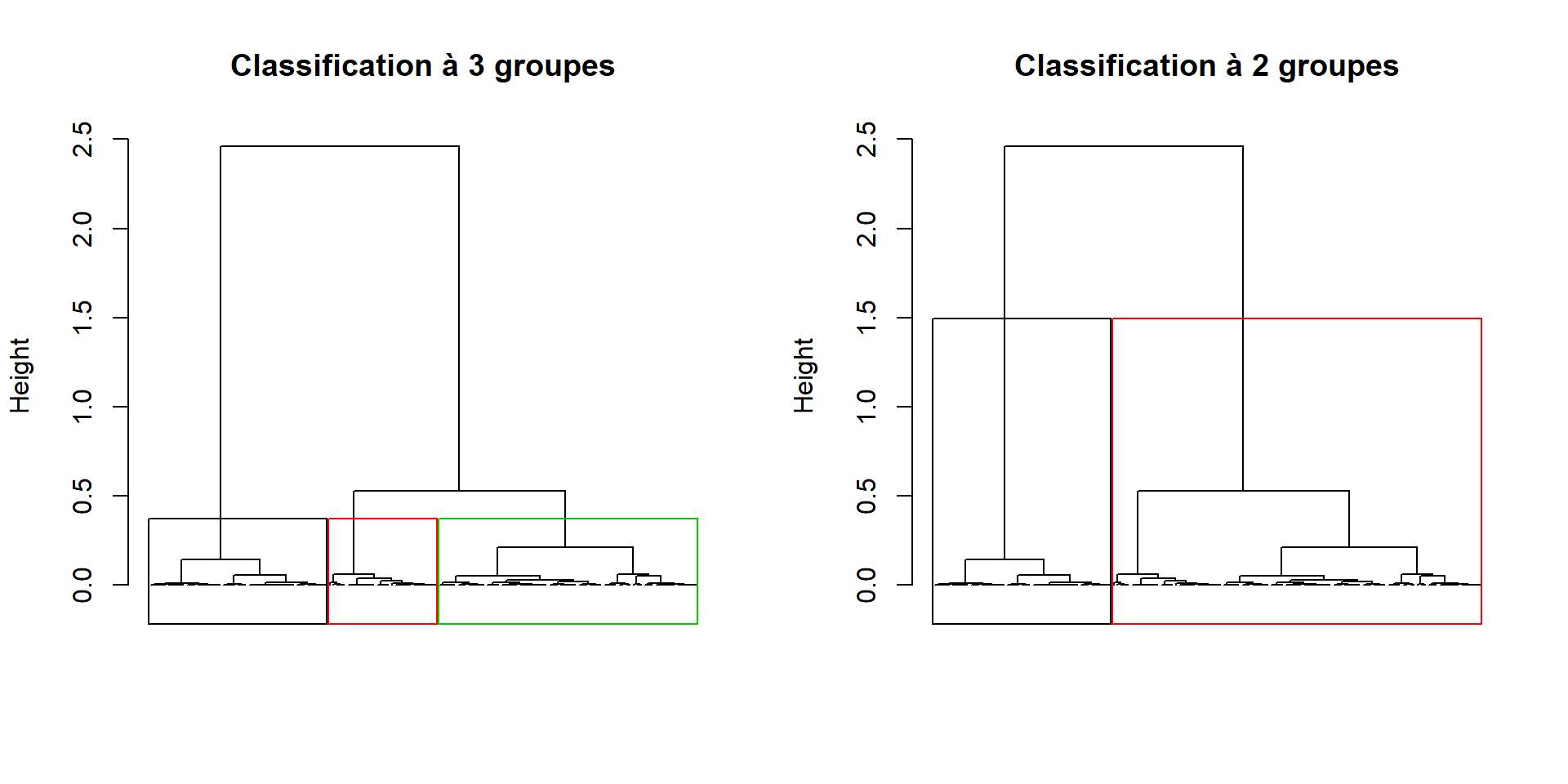

La CAH sous R (14)

Comparaison avec la méthode du lien complet :

dendro.complet = HCPC(iris.std, nb.clust = -1, 
                   consol = FALSE, method = "complete", 
                   graph = FALSE)
par(mfrow=c(1,2))
plot(dendro.ward, choice = "tree", tree.barplot = FALSE,
     main = "Dendrogramme avec Ward", labels = FALSE)
plot(dendro.complet, choice = "tree", tree.barplot = FALSE,
     main = "Dendrogramme avec lien complet", labels = FALSE)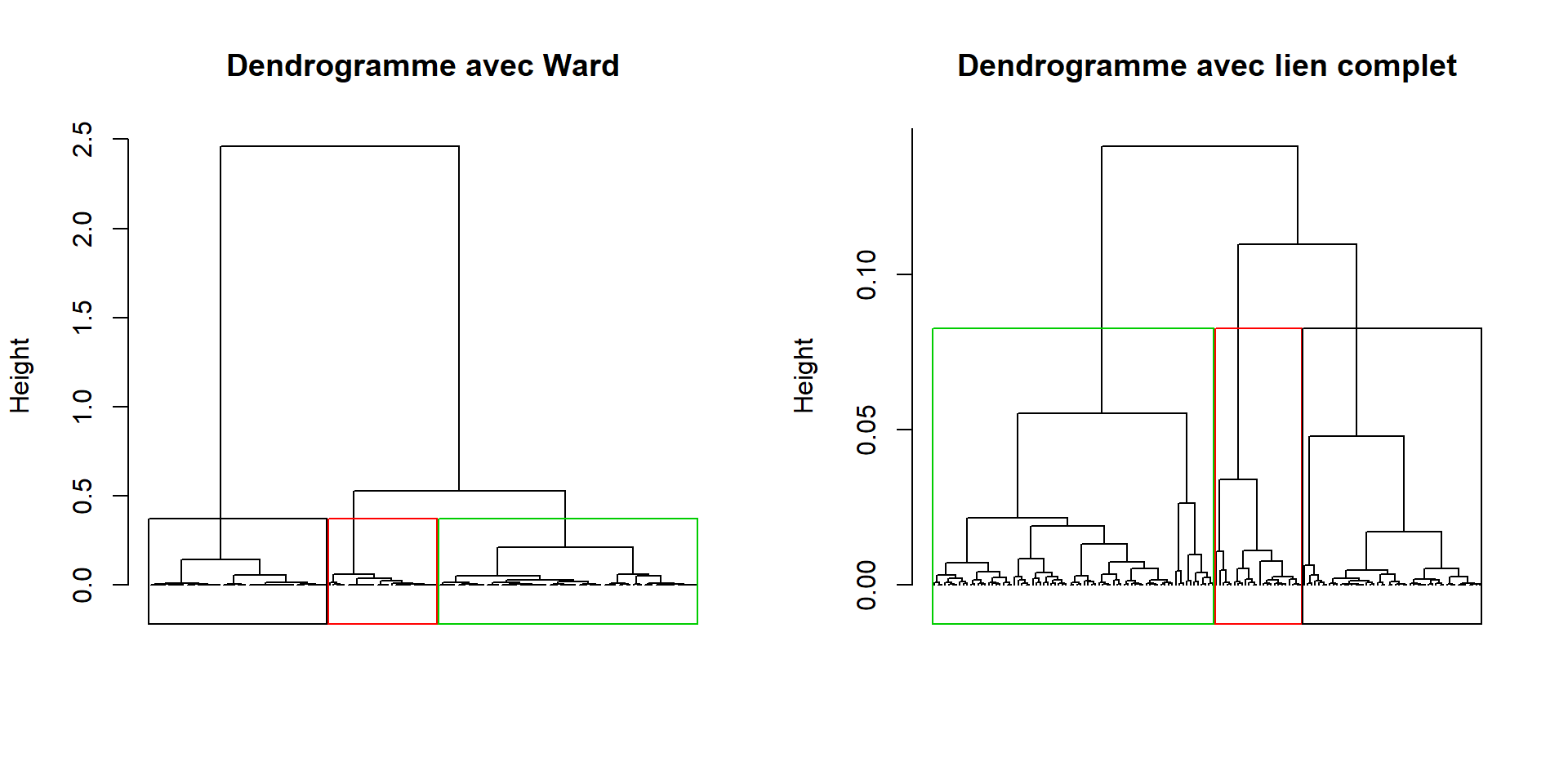

La CAH sous R (15)

Note : le choix par défaut dans la fonction plot est choice = “3D.map”, qui donne la représentation en 3D suivante :

plot(dendro.ward,
     title = "Dendrogramme avec Ward et clusters")

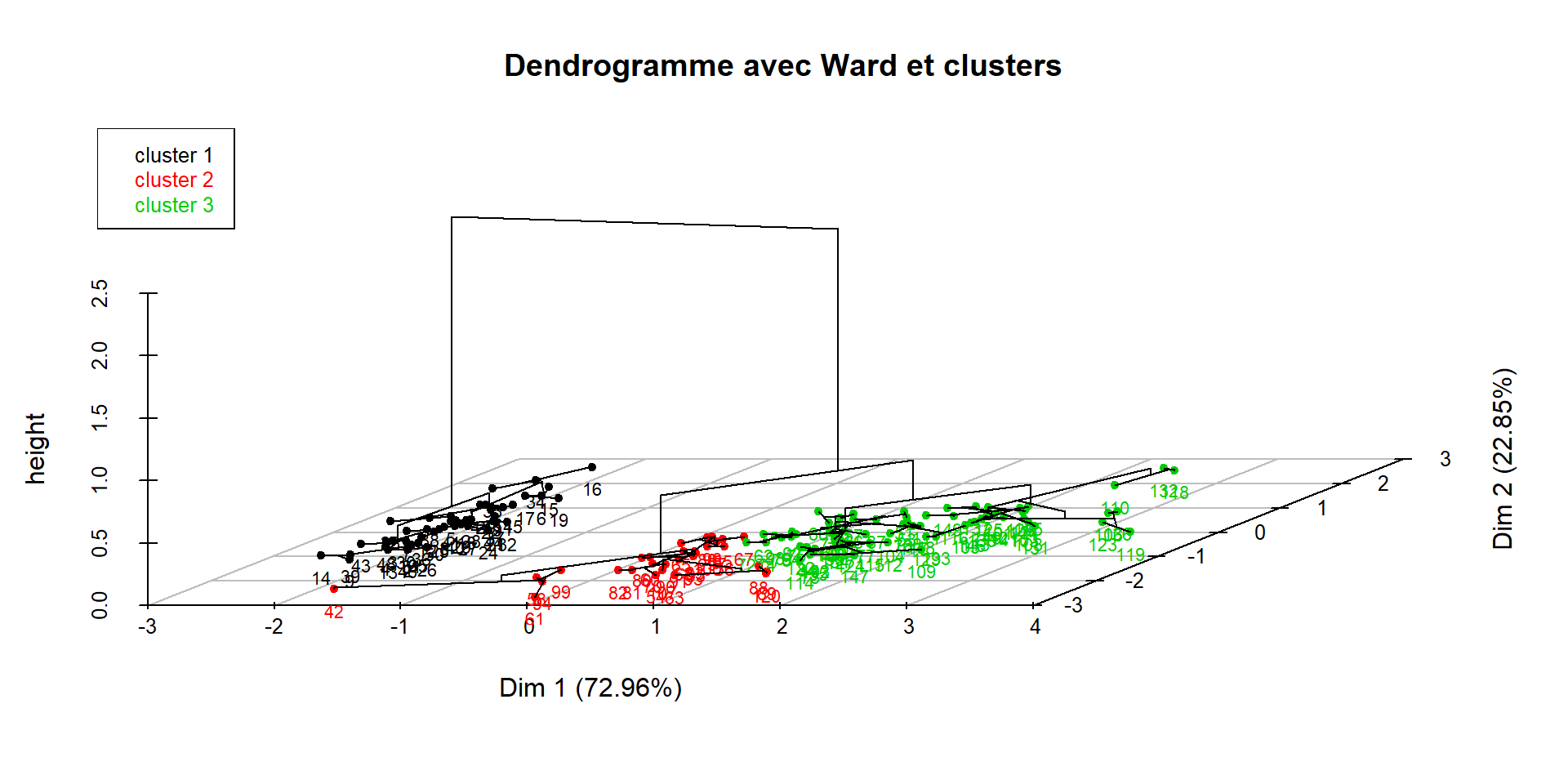
La CAH sous R (16)

Représentation de la classification par le critère de Ward sur le premier plan factoriel

plot(dendro.ward, choice = "map", 
     draw.tree = FALSE, ind.names = FALSE)

choice = “map” renvoie la projection sur le premier plan factoriel des données, avec une couleur par groupe renvoyés par le dendrogramme,
draw.tree = FALSE ne représente pas les liens de regroupements entre individus sur le plan. Par défaut, draw.tree = TRUE,
ind.names = FALSE ne représente pas les noms des observations sur les points du graphique. Par défaut, ind.names = TRUE.

La CAH sous R (17)

Résultat du code précédent

plot(dendro.ward, choice = "map", 
     draw.tree = FALSE, ind.names = FALSE)

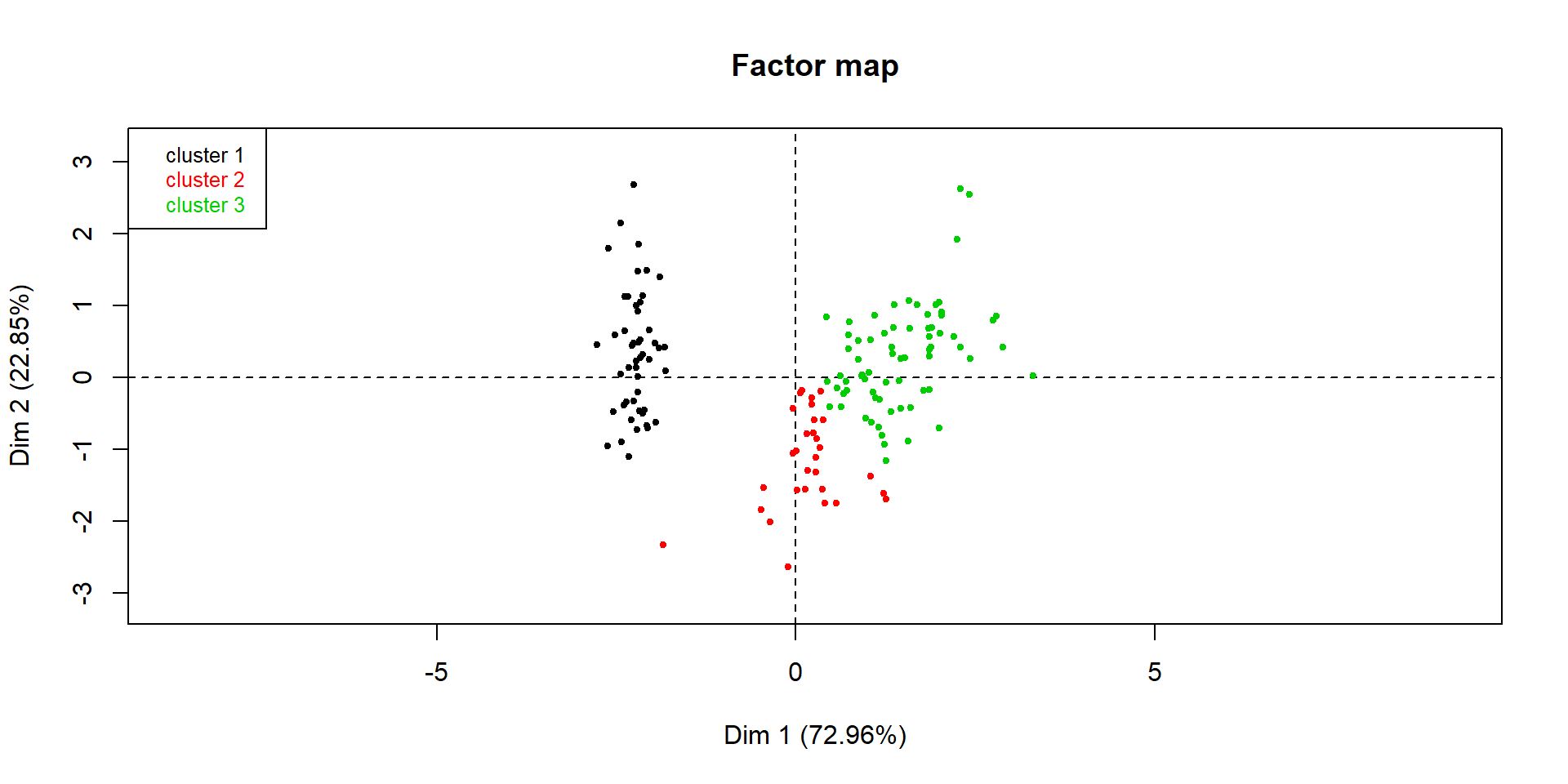
La CAH sous R (18)

Création des profils d’iris à l’aide du cercle des corrélations

plot(iris.pca, choix = "var")

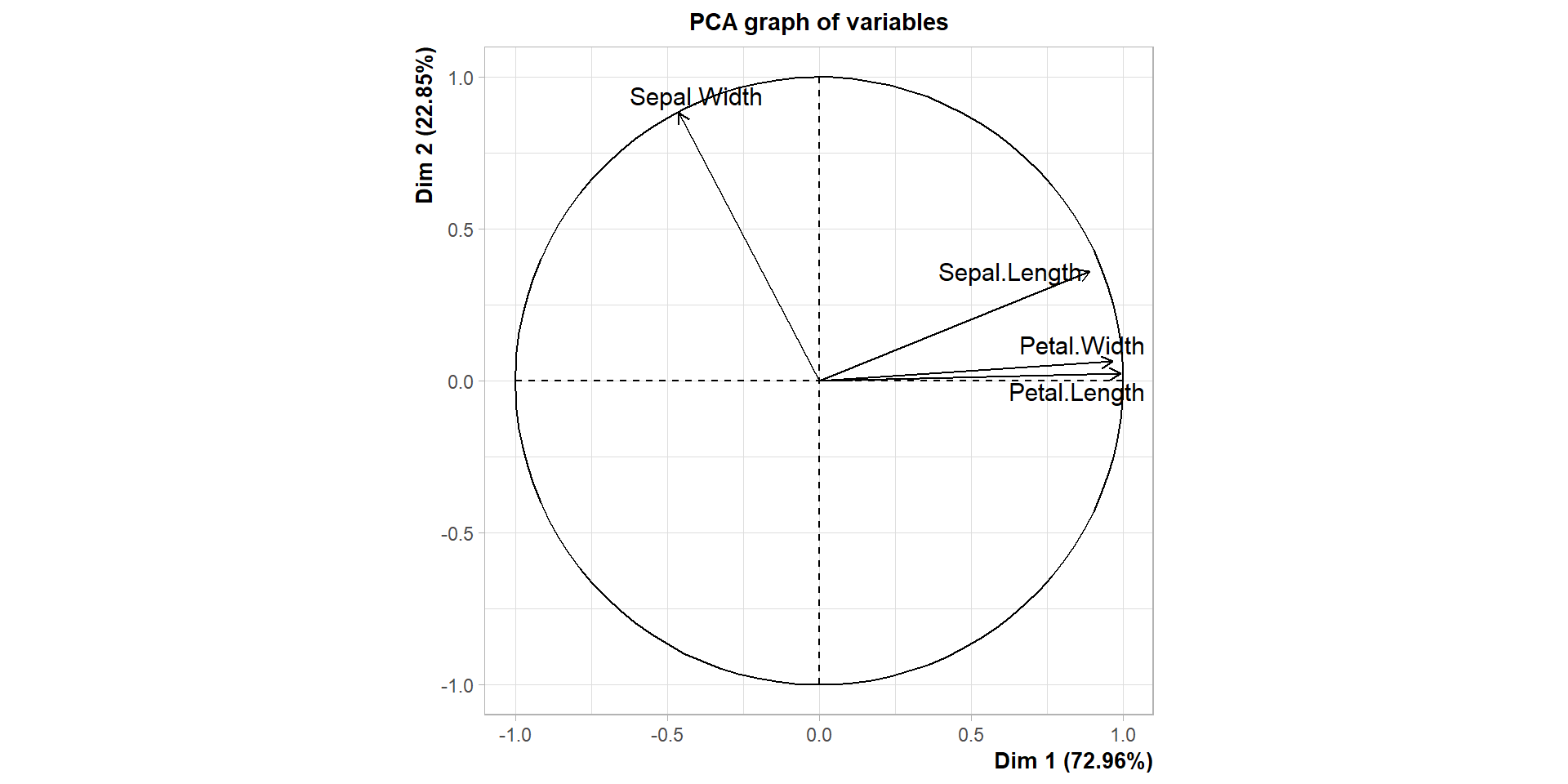
La CAH sous R (19)

Comparaison avec le critère du lien complet :

par(mfrow=c(1,2))
plot(dendro.complet, choice = "map", draw.tree = FALSE, 
     ind.names = FALSE, title = "Lien complet")
plot(dendro.ward, choice = "map", draw.tree = FALSE, 
     ind.names = FALSE, title = "Ward")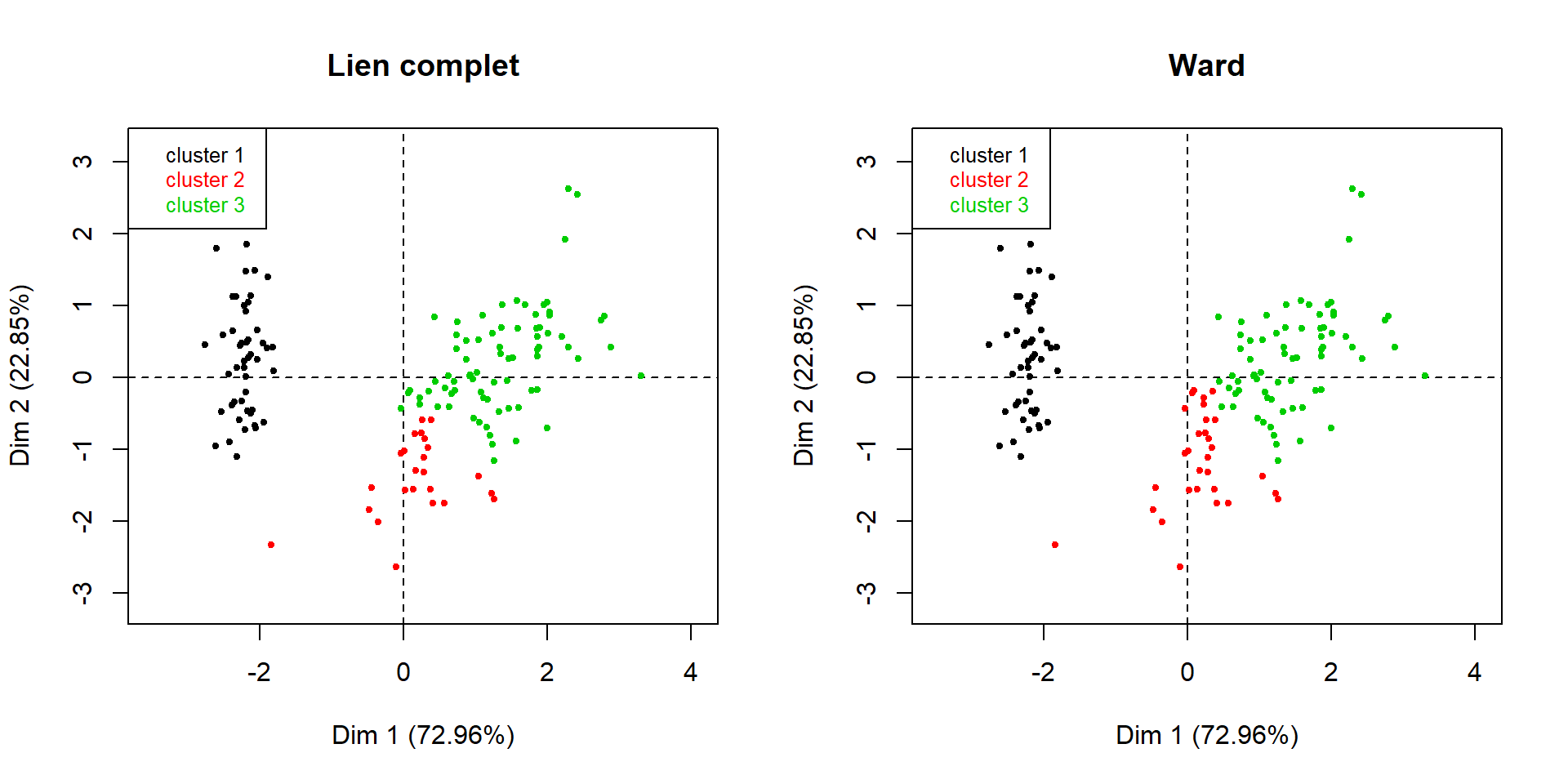

La CAH sous R (20)

Comparaison avec les espèces (où habillage indique le numéro de colonne de la variable qualitative à utiliser pour colorer les points)

plot(iris.pca, choix = "ind", label = "quali", 
     habillage = 5)

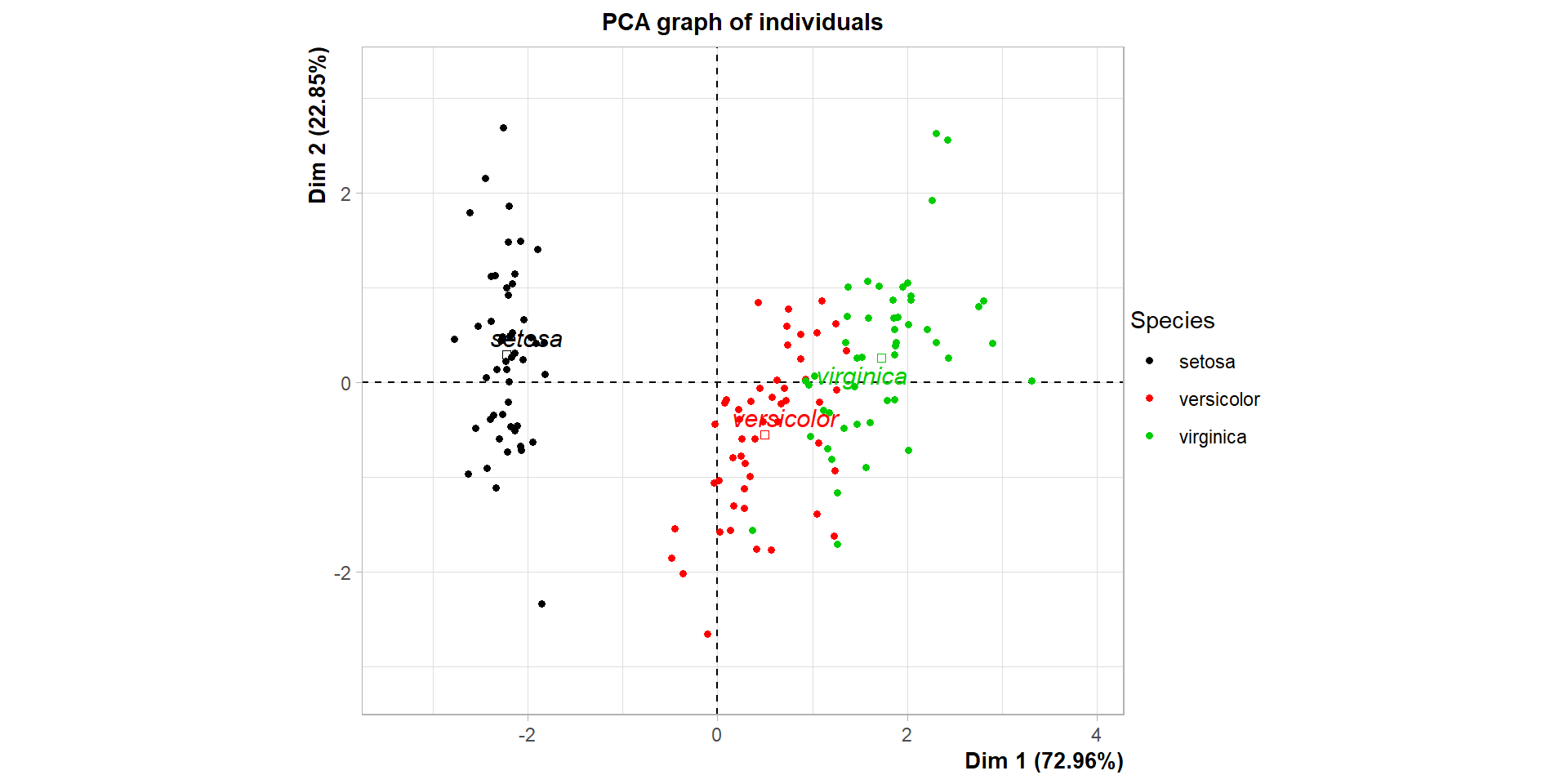
La CAH sous R (21)

Nouvelle table de données en sortie de la fonction HCPC (où le $ sélectionne l’objet data.clust dans la liste en sortie)

head(dendro.ward$data.clust)

##   Sepal.Length Sepal.Width Petal.Length Petal.Width clust
## 1   -0.8976739  1.01560199    -1.335752   -1.311052     1
## 2   -1.1392005 -0.13153881    -1.335752   -1.311052     1
## 3   -1.3807271  0.32731751    -1.392399   -1.311052     1
## 4   -1.5014904  0.09788935    -1.279104   -1.311052     1
## 5   -1.0184372  1.24503015    -1.335752   -1.311052     1
## 6   -0.5353840  1.93331463    -1.165809   -1.048667     1

Récupération de la classification :

groupes = dendro.ward$data.clust$clust
groupes

##   [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
##  [38] 1 1 1 1 2 1 1 1 1 1 1 1 1 3 3 3 2 3 2 3 2 3 2 2 3 2 3 2 3 2 2 2 2 3 3 3 3
##  [75] 3 3 3 3 3 2 2 2 2 3 2 3 3 2 2 2 2 3 2 2 2 2 2 3 2 2 3 3 3 3 3 3 2 3 3 3 3
## [112] 3 3 3 3 3 3 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
## [149] 3 3
## Levels: 1 2 3

TP : application de la CAH sur les données de satisfaction sur les villes

Charger les données sur l’enquête de satisfaction sur les villes où il fait bon vivre (fichier Villes.csv) :

satisfv = read.csv2("Donnees/Villes.csv", header = T)
x = satisfv[,-1]
rownames(x) = satisfv$ville

Ici, on nomme les observations à l’aide de la colonne 1 (idenfiant “ville”). Dans les représentations graphiques, on laissera label et ind.names par défaut afin d’avoir les noms des villes sur les graphiques.

Effectuer une ACP sur ces données, puis une CAH. Sélectionner un nombre de groupes et les représenter sur le premier plan factoriel.

TP : application de la CAH sur les données de satisfaction sur les hôtels

Charger les données sur l’enquête de satisfaction de la chaîne d’hôtels 3 étoiles (fichier Hotels.csv) :

satisfh = read.csv2("Donnees/Hotels.csv", header = T)
x = satisfh[1:46, -1]
rownames(x) = satisfh$Nom[1:46]

Pourquoi est-il judicieux de standardiser ces données, alors que ce n’est pas forcément nécessaire pour les villes ?
Refaire les analyses demandées sur le jeu de données précédent.

Centres mobiles

Algorithme dû principalement à Forgy (1965) : E. Forgy, Cluster analysis of multivariate data : Efficiency versus interpretability of classification, Biometrics, 21:768:780, 1965
Prémisses ou variantes : Thorndike (1953), k-means MacQueen (1967), Ball & Hall (1967)
Généralisation marquante : Algorithme des nuées dynamiques proposé par Diday (1971)
Adapté aux grands jeux de données :
- traitement séquentiel possible
- ne requiert pas le calcul d’une matrice $n\times n$ de distances entre individus

Algorithme (k-means)

Description de l’algorithme

$n$ individus, décrits par $p$ variables, à classifier en $k$ classes ($k$ fixé)
Etape 0 :
- $k$ centres provisoires $\{C_1^0,\ldots,C_k^0\}$ tirés au hasard.
- $k$ groupes $\{P_1^0,\ldots,P_k^0\}$ créés à partir des centres en regroupant les données les plus proches de chaque centre.
- Obtention de la classification $P^0$.
Etape j :
- $\{C_1^j,\ldots,C_k^j\}$ centres (= points moyens) des $k$ groupes $\{P_1^{j-1},\ldots,P_k^{j-1}\}$ construits à l’étape $j-1$.
- $k$ nouveaux groupes $\{P_1^j,\ldots,P_k^j\}$ créés à partir des nouveaux centres suivant la même règle qu’à l’étape 0.
- Obtention de la partition $P^j$.
Fin de l’algorithme : l’algorithme converge vers une classification stable. Arrêt lorsque la classification reste la même, ou lorsque la variance intra-classes ne décroit plus, ou encore lorsque le nombre maximal d’itérations est atteint.

Un exemple simple

$k=2$ classes, centres initiaux choisis au hasard, par exemple A et B.

Etape 0 :

C1 = A attire le point A
C2 = B attire les points B, C, D et E.
$\Longrightarrow$ Nouveaux centres : C1 (1 ; 9) et C2 (6,5 ; 3,5)

Un exemple simple (2)

Etape 1 :

C1 attire les point A et B
C2 attire les points C, D et E.
$\Longrightarrow$ Nouveaux centres : C1 (1 ; 8,5) et C2 (8,3 ; 2)

Un exemple simple (3)

Etape 2 :

Mêmes classes que précédemment $\Longrightarrow$ la méthode s’arrête.

Atouts et limites des méthodes

Atouts et limites de la CAH
- Atouts : fournit à la fois les classes et leur nombre.
- Limites :
  - Souvent malaisé de choisir la coupure significative sur le dendrogramme
  - Partition non-optimale en raison de sa structure hiérarchique
  - Fort coût algorithmique lorsque $n$ devient grand
Atouts et limites des centres mobiles
- Atouts :
  - Coût algorithmique faible
  - Traitement séquentiel
- Limites :
  - Nombre de classes fixé a priori
  - Partition obtenue fortement dépendante des centres provisoires des classes
Idée : Mixer les 2 méthodes (CAH et centres mobiles)

Classification mixte

Etape préliminaire si $n$ est grand : Classification en $q$ classes, avec $n>>q$ ($>>k$ le nombre de classes final désiré), en utilisant la méthode des centres mobiles.
Etape 1 : Classification ascendante hiérarchique sur les $q$ éléments (centres) obtenus à l’étape précédente, ou directement sur les données si $n$ est petit.

$\Longrightarrow$ Choix du nombre $k$ de groupes pour la classification.
Etape 2 : Optimisation par les centres mobiles avec $k$ classes, appliqué sur les $n$ individus originels.

Centres mobiles sous R : exemple des Iris de Fisher

Choix du nombre de classes (cf. CAH) : $2$ ou $3$. Application des centres mobiles ($k$-means ou $k$-moyennes):

iris.std = data.frame(scale(iris[,-5]))
km2 = kmeans(iris.std, 2, nstart = 10)
km3 = kmeans(iris.std, 3, nstart = 10)

L’option “nstart” permet de stabiliser la méthode vis à vis de l’initialisation des centres. Statistiques et classification obtenues:

names(km2)

## [1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
## [6] "betweenss"    "size"         "iter"         "ifault"

Centres mobiles sous R (2)

Eléments utiles en sortie de la fonction kmeans:

Le vecteur des groupes associant à chaque observation le numéro du groupe auquel elle appartient :

km2$cluster

##   [1] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
##  [38] 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
##  [75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [112] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
## [149] 1 1

Coordonnées des centres de groupes :

km2$centers

##   Sepal.Length Sepal.Width Petal.Length Petal.Width
## 1    0.5055957  -0.4252069     0.650315   0.6253518
## 2   -1.0111914   0.8504137    -1.300630  -1.2507035

Centres mobiles sous R (3)

Effectifs dans chaque groupe :

km2$size

## [1] 100  50

Variances dans chaque groupe :

km2$withinss

## [1] 173.52867  47.35062

Variance intra-groupes (somme de withinss) :

km2$tot.withinss

## [1] 220.8793

Centres mobiles sous R (4)

Variance inter-groupes :

km2$betweenss

## [1] 375.1207

Variance totale (tot.withinss+betweenss) :

km2$totss

## [1] 596

Classification mixte sous R

Représentation de la classification mixte (CAH+Centres mobiles) à $2$ classes sur le premier plan factoriel : on consolide dans la fonction HCPC en indiquant le nombre de groupes souhaité (ici nb.clust=2) et consol = TRUE (valeur par défaut) :

dendro.ward2 = HCPC(iris.std, nb.clust = 2, graph = FALSE)
plot(dendro.ward2, choice = "map", 
     draw.tree = FALSE, ind.names = FALSE)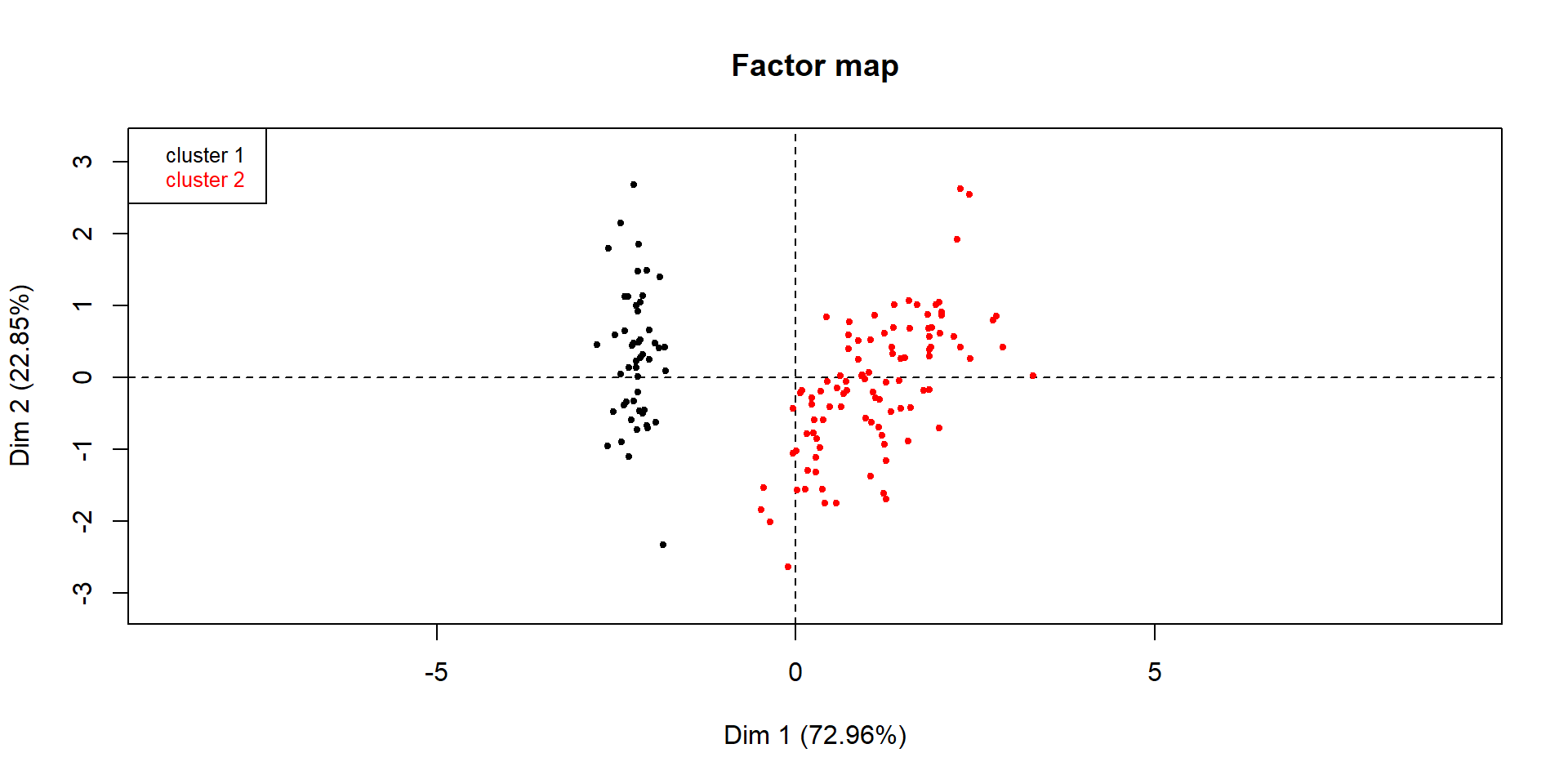

Classification mixte sous R (2)

Note 1 : en mettant nb.clust = -1 dans HCPC, on obtient la classification dite “optimale” avec choix automatique du nombre de classes à partir du dendrogramme

dendro.ward = HCPC(iris.std, nb.clust = -1, graph = FALSE)
plot(dendro.ward, choice = "map", 
     draw.tree = FALSE, ind.names = FALSE)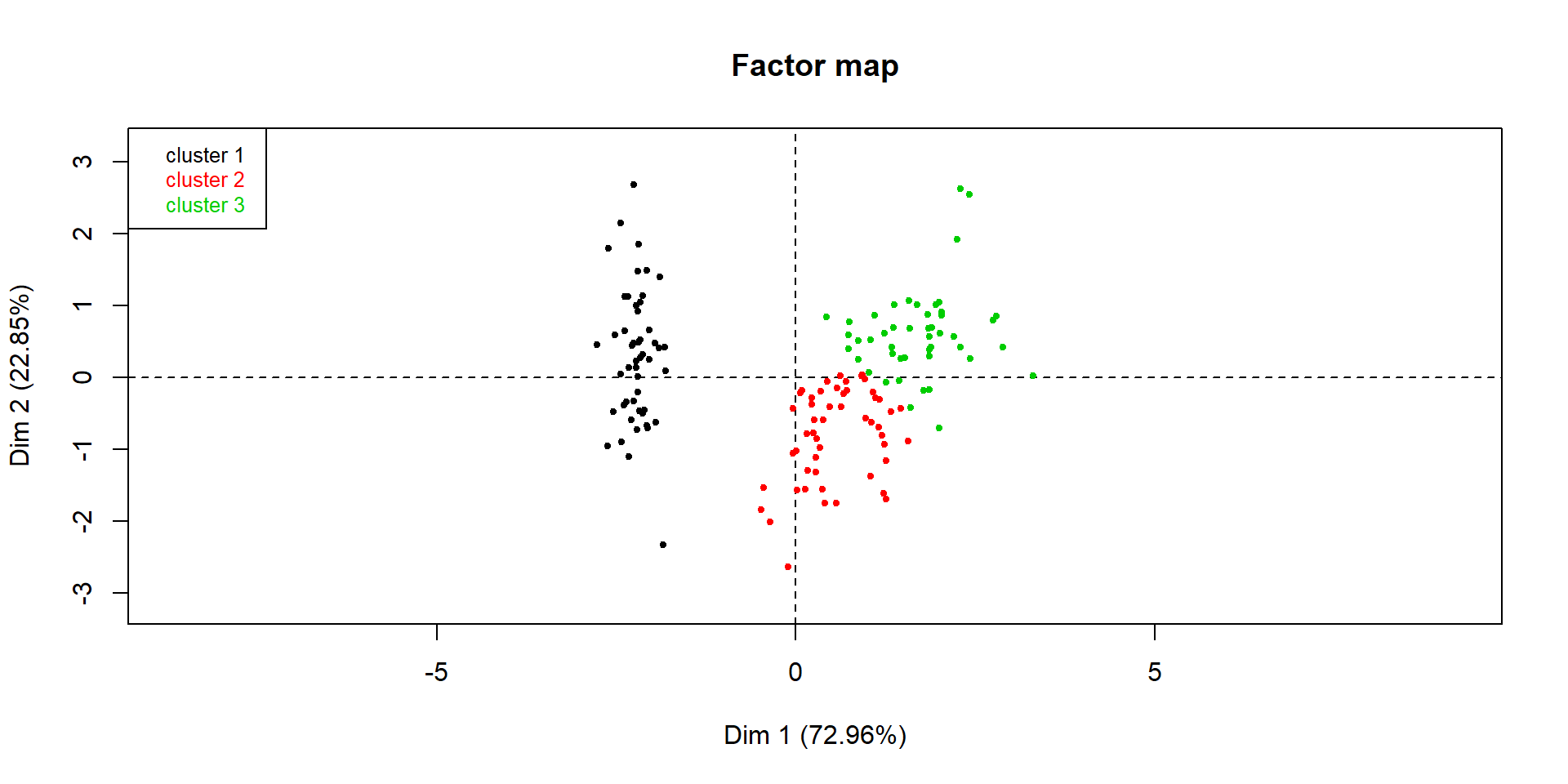

Classification mixte sous R (3)

Comparaison avec les espèces

plot(iris.pca, choix = "ind",
     habillage = 5, label = "quali")

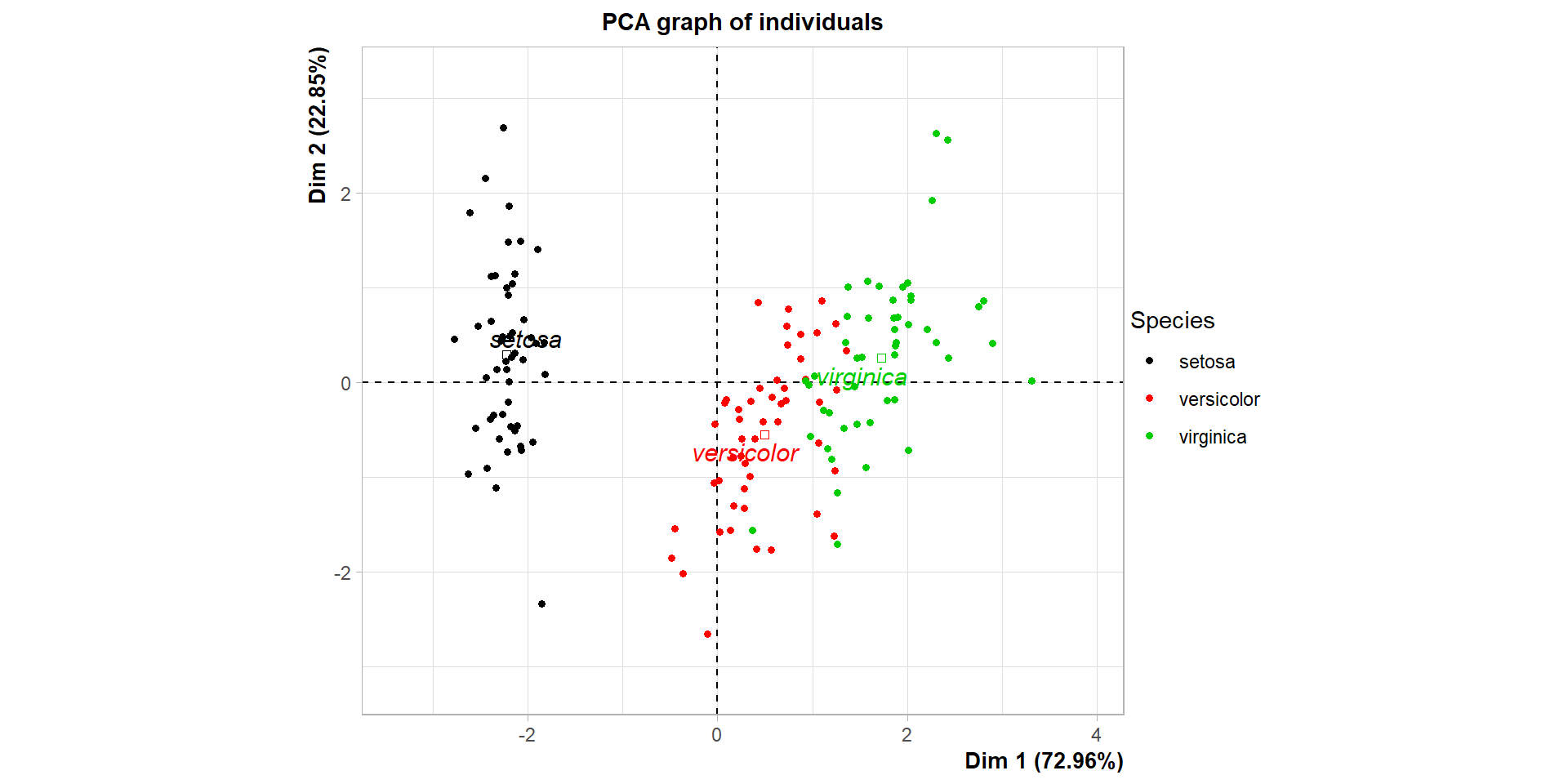
Classification mixte sous R (4)

Note 2 : en ne fixant aucune option dans plot, on obtient la représentation dans le premier plan factoriel, ainsi que le dendrogramme

dendro.ward = HCPC(iris.std, nb.clust = -1, graph = FALSE)
plot(dendro.ward, 
     title = "Dendrogramme avec Ward et clusters")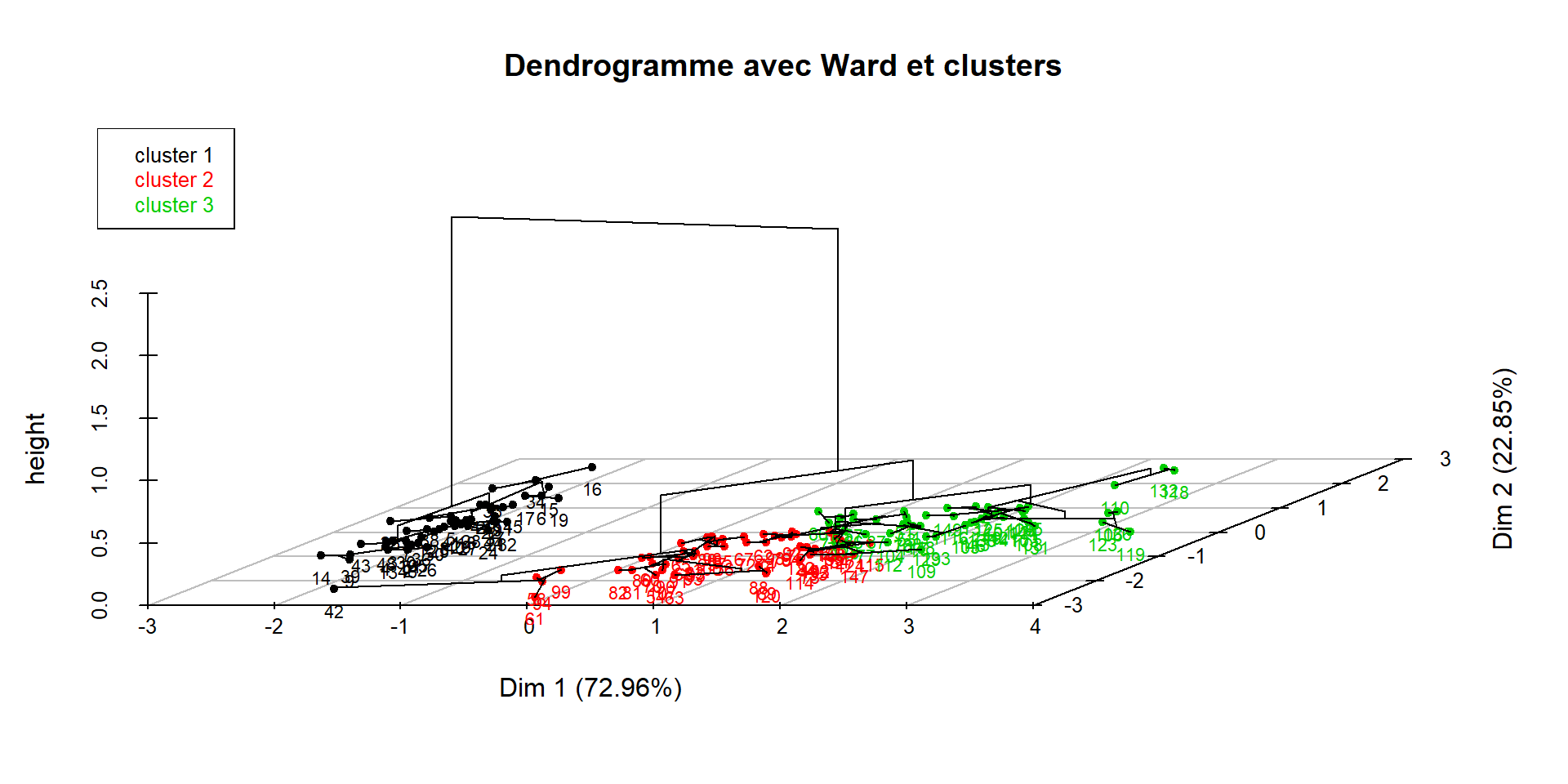

Classification mixte sous R (5)

Afin de réduire le nombre de données si la base est trop grande (étape préliminaire de la classification mixte), on fixe l’option kk = < nb de classes désiré > dans la fonction HCPC (par exemple, si $n>10000$, on peut fixer kk = 1000 dans HCPC). Attention ! Dans ce cas, HCPC ne fait pas de consolidation, et il faut donc faire passer un kmeans ensuite (étape 2 de la classification mixte) pour effectuer la consolidation soi-même.
Si la consolidation a été faite en-dehors de HCPC avec kmeans, voici un exemple de code pour représenter les groupes sur le premier plan factoriel (où habillage impose de mettre une couleur par individu, et col.hab définit quelle couleur est utilisée pour chaque individu. Ici, 2 couleurs, une par groupe)

plot(iris.pca, choix="ind", label = "quali", 
     habillage = "ind", col.hab=km2$cluster)

Si le nombre de données n’est pas trop grand, la fonction HCPC fait la classification mixte par défaut

TP : application de la classification mixte sur les données de satisfaction sur les villes

Charger les données sur l’enquête de satisfaction sur les villes où il fait bon vivre (fichier Villes.csv) :

satisfv = read.csv2("Donnees/Villes.csv", header = T)
x = satisfv[,-1]
rownames(x) = satisfv$ville

Refaire une classification mixte, avec le nombre de groupes choisi à l’issue de la CAH.
Représenter les groupes obtenus sur le premier plan factoriel, et effectuer un profilage des villes suivant les caractéristiques évaluées.

TP : application de la classification mixte sur les données de satisfaction sur les hôtels

Charger les données sur l’enquête de satisfaction de la chaîne d’hôtels 3 étoiles (fichier Hotels.csv) :

satisfh = read.csv2("Donnees/Hotels.csv", header = T)
x = satisfh[1:46, -1]
rownames(x) = satisfh$Nom[1:46]

Refaire les analyses demandées sur le jeu de données précédent.
Croiser les profils obtenus avec les villes où sont situées les hôtels évalués.

Classification sur facteurs

Variables quantitatives : Analyse en Composantes Principales (ACP).
- Elimination des fluctuations aléatoires (= bruit de mesures) constituant l’essentiel de la variance prise en compte par les derniers axes.
- Lissage des données.
- Production de groupes plus homogènes.
Variables qualitatives : Analyse des Correspondances Multiples (ACM).
- Transformation des variables en variables quantitatives via un tableau disjonctif complet.
Remarque : ACM nécessaire pour intégrer les variables qualitatives à la classification, par contre ACP pas toujours utile pour les variables quantitatives.

Passer aux coordonnées factorielles

Sélection d’un sous-espace factoriel de dimension suffisante $q<p$,
Classification des $n$ individus représentés par leurs composantes sur les $q$ premiers axes factoriels.
Remarque : équivalence entre les classifications des $n$ individus sur l’ensemble
- des $p$ variables,
- des $p$ facteurs issus d’une analyse factorielle, seule la représentation des données change (changement de base).
Attention : si l’ACP est effectuée sur la matrice des corrélations, cela revient à standardiser les variables

$\Longrightarrow$ inutile de standardiser les facteurs avant d’effectuer la classification.

Classification sur facteurs sous R : Iris de Fisher

Sélection des $q$ facteurs sur lesquels la classification est effectuée

library(factoextra)
iris.pca = PCA(iris, ncp = 4, quali.sup = 5, graph = FALSE)
fviz_eig(iris.pca, choice = "variance", 
         addlabels = TRUE)+geom_hline(yintercept = 1)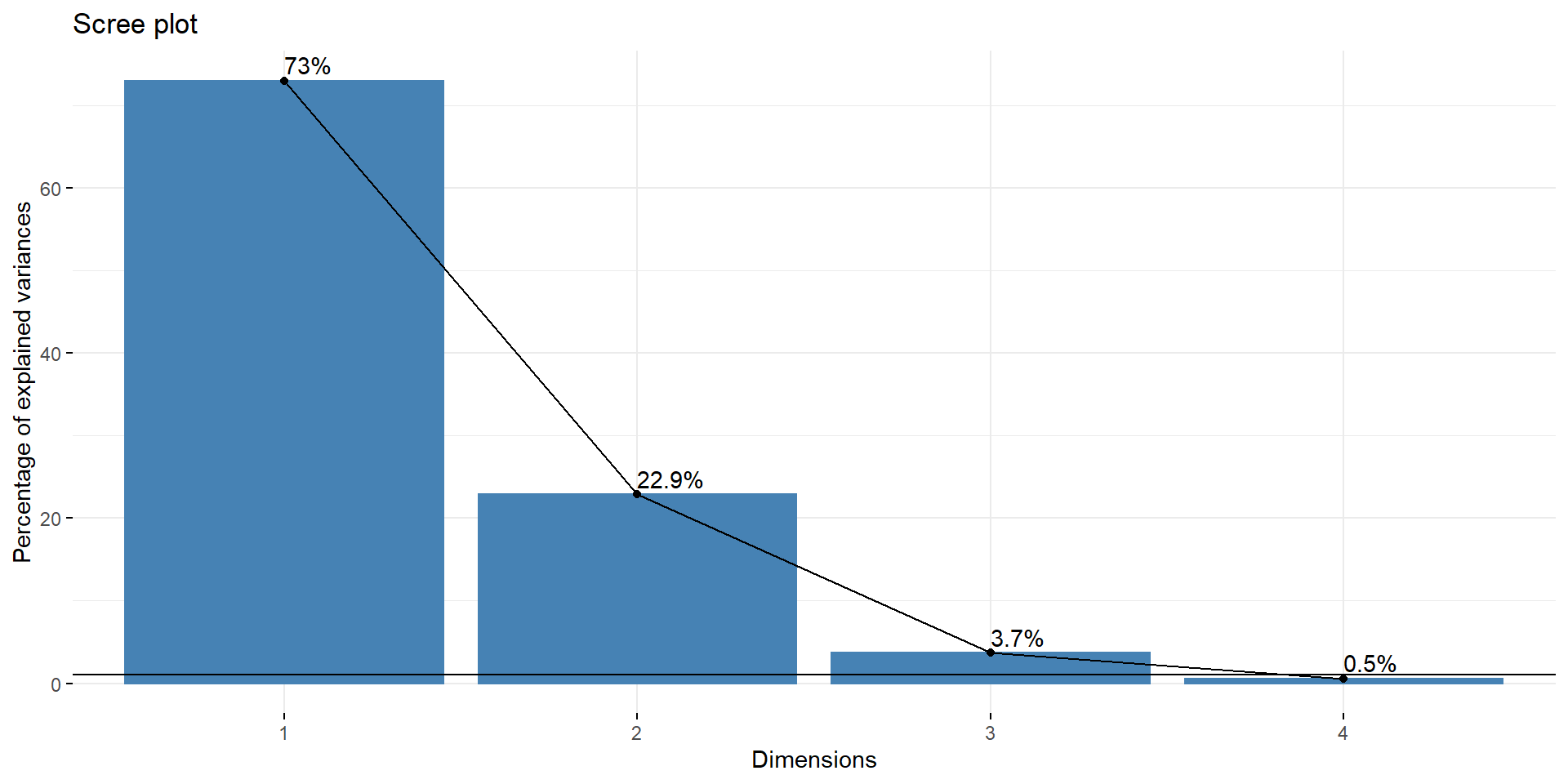

Classification sur facteurs sous R (2)

La fonction HCPC peut prendre en entrée soit un jeu de données (dataframe), soit un objet créé par les fonctions PCA (ACP) ou MCA (ACM) de FactoMineR. Donc :

Soit on effectue la classification mixte directement sur les composantes principales $1$ et $2$ :

facteurs = data.frame(iris.pca$ind$coord[,1:2])

Soit on refait tourner la fonction PCA ou MCA avec le nombre de facteurs choisis (option ncp = )

facteurs = PCA(iris, ncp = 2, quali.sup = 5, graph = FALSE)

Dendrogramme issu de la CAH sur les facteurs de l’ACP :

dendro = HCPC(facteurs, nb.clust = -1, graph = FALSE)
plot(dendro, choice = "tree", rect = FALSE,
     labels = FALSE)

Classification sur facteurs sous R (3)

Résultat du code précédent :

dendro = HCPC(facteurs, nb.clust = -1, graph = FALSE)
plot(dendro, choice = "tree", rect = FALSE,
     labels = FALSE)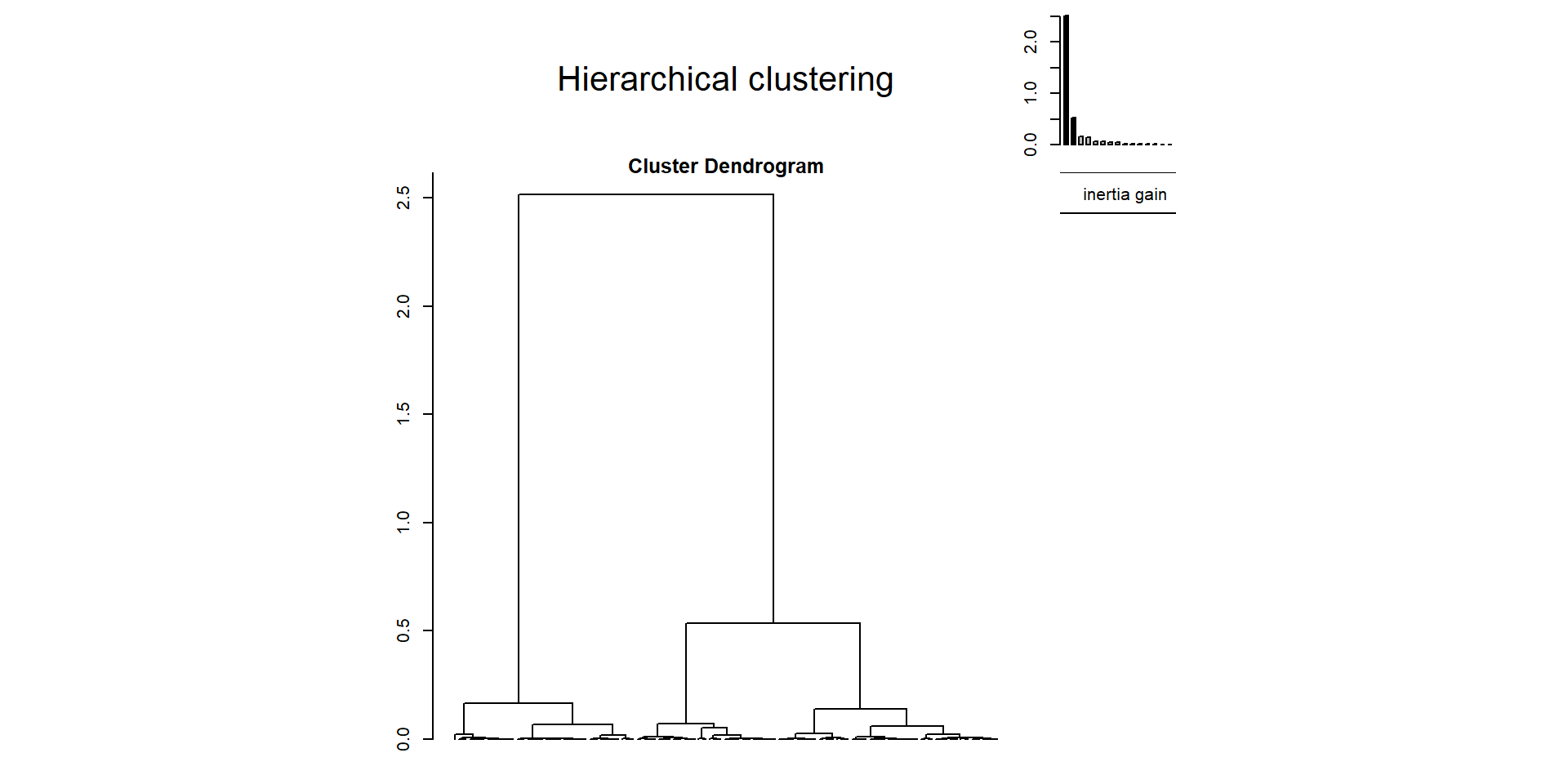

Classification sur facteurs sous R (4)

Représentation dans le premier plan factoriel :

par(mfrow=c(1,2))
plot(dendro, choice = "map", draw.tree = FALSE, 
     ind.names = FALSE, title = "Classification sur facteurs")
plot(dendro.ward, choice = "map", draw.tree = FALSE, 
     ind.names = FALSE, title = "Classification sur les données")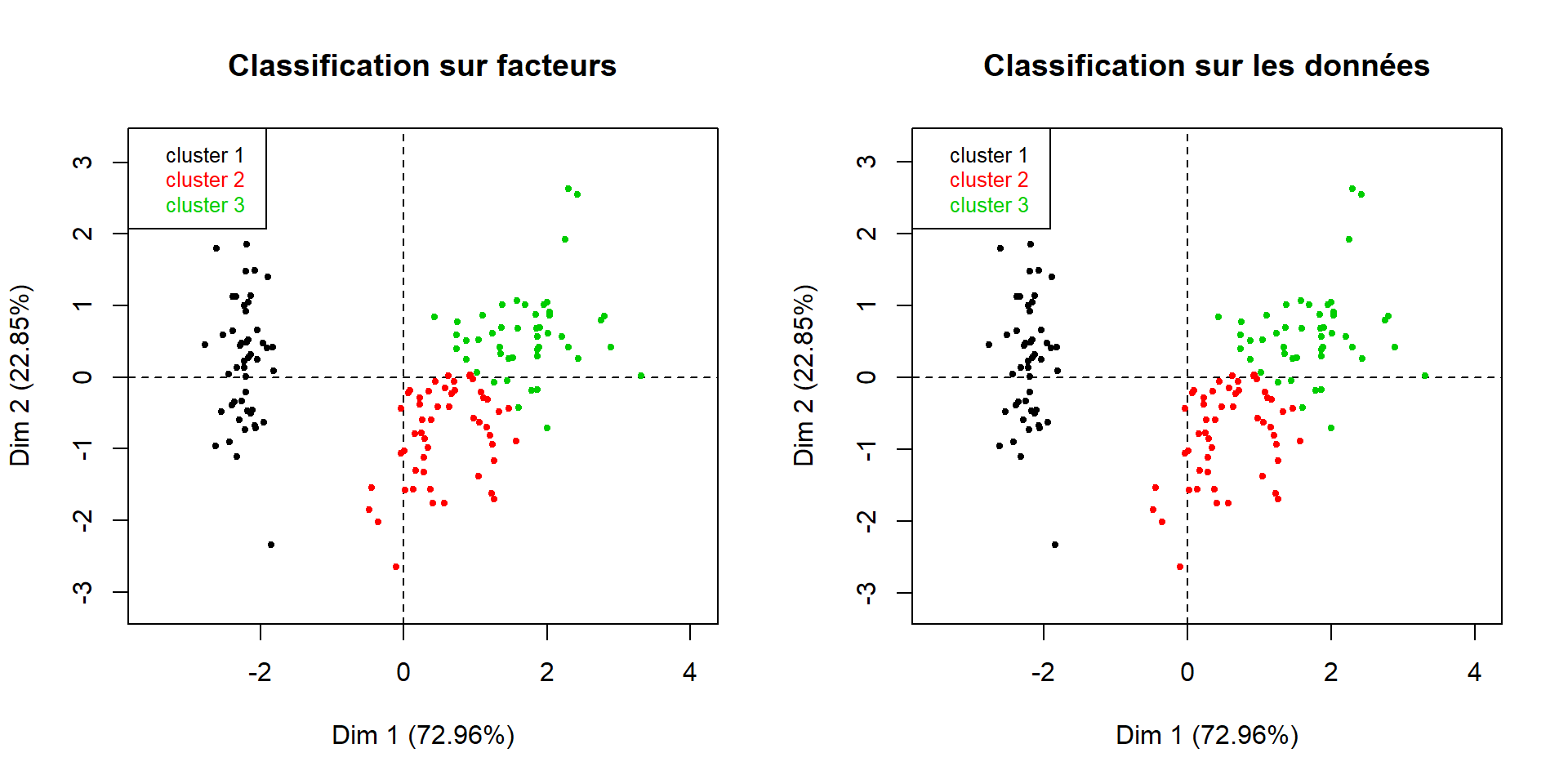

Classification mixte avec R : à retenir

Si le nombre d’observations n’est pas trop grand :
- effectuer la classification mixte sur les données standardisées, ou sur les composantes principales choisies, avec la fonction HCPC,
- choisir un nombre de groupes (si le nombre optimal fourni par HCPC ne convient pas),
- faire les profils et les représentations graphiques souhaitées directement à partir des sorties de HCPC.
Si le nombre d’observations est trop grand :
- effectuer la classification mixte sur les données standardisées, ou sur les composantes principales choisies, avec la fonction HCPC et l’option kk=,
- consolider la classification avec la fonction kmeans, où le nombre de groupes est issu de HCPC, ou choisi à partir du dendrogramme,
- faire les profils et les représentations graphiques souhaitées à partir des sorties de PCA et kmeans.

TP : Classification sur facteurs pour les données de satisfaction sur les villes et les hôtels

Effectuer la classification sur facteurs sur les données de satisfaction sur les villes (fichier Villes.csv) :

satisfv = read.csv2("Donnees/Villes.csv", header = T)
x = satisfv[,-1]
rownames(x) = satisfv$ville

Effectuer la classification sur facteurs sur les données de satisfaction sur les hôtels (fichier Hotels.csv) :

satisfh = read.csv2("Donnees/Hotels.csv", header = T)
x = satisfh[1:46, -1]
rownames(x) = satisfh$Nom[1:46]

Comparer les profils obtenus avec ceux produits par la classification sur les données d’origine.
Dans chaque cas, décider si le débruitage était utile, et expliquer pourquoi.

Classification automatique : Méthodes et mise en application

Arthur Leroy - Université de Paris

DU Dataviz - 7 et 8 Avril 2021

Coordonnées et références

Planning de la journée

Introduction

Table de données brutes

Visualisation des données sur le premier plan factoriel

Visualisation des groupes sur le premier plan factoriel

Classification automatique

Méthodes de classification automatique

Méthodes et Mise en Oeuvre

Classification Ascendante Hiérarchique

Représentation graphique

Représentation graphique (2)

CAH : l’algorithme de base

Agrégation de groupes

Dissemblance : les choix

Dissemblance : les choix (2)

Critère de Ward

Décomposition de l’inertie (LMP)

Qualité d’une classification (LMP)

Algorithme d’agrégation par critère de Ward

Un exemple simple

Un exemple simple (2)

Un exemple simple (3)

Un exemple simple (4)

Choix du nombre de groupes

Choix du nombre de groupes : exemple

Création des profils d’individus

La CAH sous R : exemple des Iris de Fisher

La CAH sous R (2)

La CAH sous R (3)

La CAH sous R (4)

La CAH sous R (5)

La CAH sous R (6)

La CAH sous R (7)

La CAH sous R (8)

La CAH sous R (9)

La CAH sous R (10)

La CAH sous R (11)

La CAH sous R (12)

La CAH sous R (13)

La CAH sous R (14)

La CAH sous R (15)

La CAH sous R (16)

La CAH sous R (17)

La CAH sous R (18)

La CAH sous R (19)

La CAH sous R (20)

La CAH sous R (21)

TP : application de la CAH sur les données de satisfaction sur les villes

TP : application de la CAH sur les données de satisfaction sur les hôtels

Centres mobiles

Algorithme (k-means)

Description de l’algorithme

Un exemple simple

Un exemple simple (2)

Un exemple simple (3)

Atouts et limites des méthodes

Classification mixte

Centres mobiles sous R : exemple des Iris de Fisher

Centres mobiles sous R (2)

Centres mobiles sous R (3)

Centres mobiles sous R (4)

Classification mixte sous R

Classification mixte sous R (2)

Classification mixte sous R (3)

Classification mixte sous R (4)

Classification mixte sous R (5)

TP : application de la classification mixte sur les données de satisfaction sur les villes

TP : application de la classification mixte sur les données de satisfaction sur les hôtels

Classification sur facteurs

Passer aux coordonnées factorielles

Classification sur facteurs sous R : Iris de Fisher

Classification sur facteurs sous R (2)

Classification sur facteurs sous R (3)

Classification sur facteurs sous R (4)

Classification mixte avec R : à retenir

TP : Classification sur facteurs pour les données de satisfaction sur les villes et les hôtels

Classification automatique :
Méthodes et mise en application