A Bayesian Framework for Multivariate Differential Analysis accounting for Missing Data

Abstract

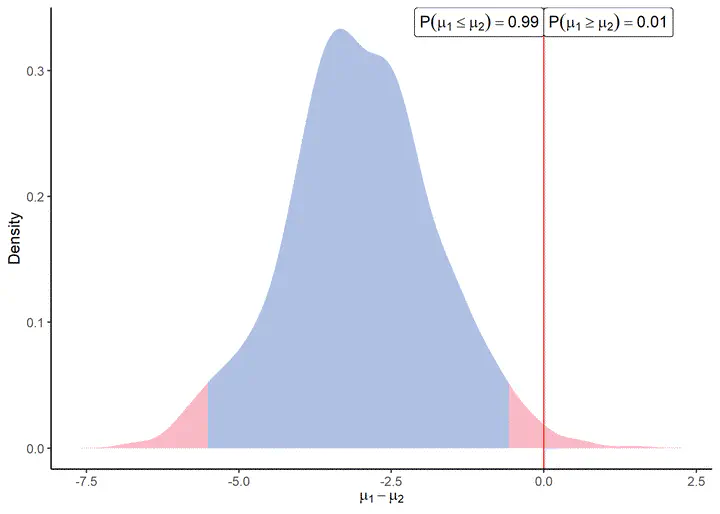
Current statistical methods in differential proteomics analysis generally leave aside several challenges, such as missing values, correlations between peptide intensities and uncertainty quantification. Moreover, they provide point estimates, such as the mean intensity for a given peptide or protein in a given condition. The decision of whether an analyte should be considered as differential is then based on comparing the p-value to a significance threshold, usually 5%. In the state-of-the-art limma approach, a hierarchical model is used to deduce the posterior distribution of the variance estimator for each analyte. The expectation of this distribution is then used as a moderated estimation of variance and is injected directly into the expression of the t-statistic. However, instead of merely relying on the moderated estimates, we could provide more powerful and intuitive results by leveraging a fully Bayesian approach and hence allow the quantification of uncertainty. The present work introduces this idea by taking advantage of standard results from Bayesian inference with conjugate priors in hierarchical models to derive a methodology tailored to handle multiple imputation contexts. Furthermore, we aim to tackle a more general problem of multivariate differential analysis, to account for possible inter-peptide correlations. By defining a hierarchical model with prior distributions on both mean and variance parameters, we achieve a global quantification of uncertainty for differential analysis. The inference is thus performed by computing the posterior distribution for the difference in mean peptide intensities between two experimental conditions. In contrast to more flexible models that can be achieved with hierarchical structures, our choice of conjugate priors maintains analytical expressions for direct sampling from posterior distributions without requiring expensive MCMC methods.