Multi-Mean Gaussian Processes: A novel probabilistic framework for multi-correlated functional data

Abstract

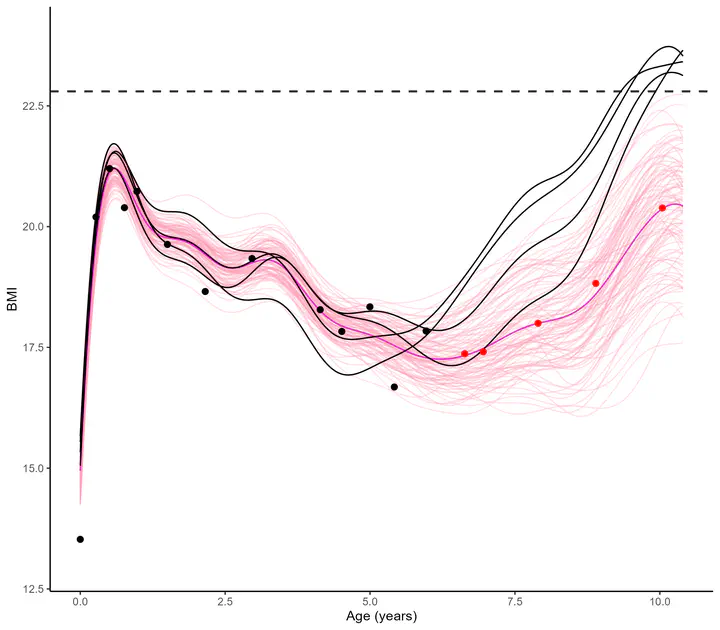
Modelling and forecasting time series, even with a probabilistic flavour, is a common and well-handled problem nowadays. However, suppose now that one is collecting data from hundreds of individuals, each of them gathering thousands of gene-related measurements, all evolving continuously over time. Such a context, frequently arising in biological or medical studies, quickly leads to highly correlated datasets where dependencies come from different sources (temporal trend, gene or individual similarities, for instance). Explicit modelling of overly large covariance matrices accounting for these underlying correlations is generally unreachable due to theoretical and computational limitations. Therefore, practitioners often need to restrict their analysis by working on subsets of data or making arguable assumptions (fixing time, studying genes or individuals independently, …). To tackle these issues, we recently proposed a new framework for multi-task Gaussian processes, tailored to handle multiple time series simultaneously. By sharing information between tasks through a mean process instead of an explicit covariance structure, this method leads to a learning and forecasting procedure with linear complexity in the number of tasks. The resulting predictions remain Gaussian distributions and thus offer an elegant probabilistic approach to deal with correlated time series. Finally, we will present the current development of an extended framework in which as many sources of correlation as desired can be considered (multiple individuals and genes could be handled jointly, for example), while maintaining linear complexity scaling. Intuitively, the approach leverages multiple latent mean processes, each being estimated with an adequate subset of data, and leads to an adaptive prediction for each individual associated with a mean process specific to the considered correlation.