Apprentissage de données fonctionnelles par modèles multi-tâches :
Application à la prédiction de performances sportives
Arthur Leroy
encadré par
- Servane Gey - MAP5, Université de Paris
- Benjamin Guedj - Inria - University College London
- Pierre Latouche - MAP5, Université de Paris
Soutenance de thèse - 09/12/2020
Origins of the thesis
A problem:
- Several papers (Boccia & al - 2017, Kearney & Hayes - 2018) point out limits of focusing on best performers in young categories.
- Sport experts seek new objecive criteria for talent identification.
An opportunity:
-
The French Swimming Federation (FFN) provides a massive database gathering most of the national competition's results since 2002.
Data
Performances in competition for FFN members:
Data
Performances in competition for FFN members:
- Irregular time series (in number of observations and location),
- Many different swimmers per category,
Data
Performances in competition for FFN members:
- Irregular time series (in number of observations and location),
- Many different swimmers per category,
- A few observations per swimmer.
Contributions
Are there different patterns of progression among swimmers?
Chapter 2
Leroy et al. - Functional Data Analysis in Sport Science: Example of Swimmers’ Progression Curves Clustering - Applied Sciences - 2018
Can we provide probabilistic predictions of future performances?
Chapter 3
Leroy et al. - Magma: Inference and Prediction with Multi-Task Gaussian Processes - Under submission in Statistics and Computing - https://github.com/ArthurLeroy/MAGMA
May possible group structures improve the quality of predictions?
Chapter 4
Leroy et al. - Cluster-Specific Predictions with Multi-Task Gaussian Processes - Under submission in JMLR - https://github.com/ArthurLeroy/MAGMAclust
Contributions
Are there different patterns of progression among swimmers?
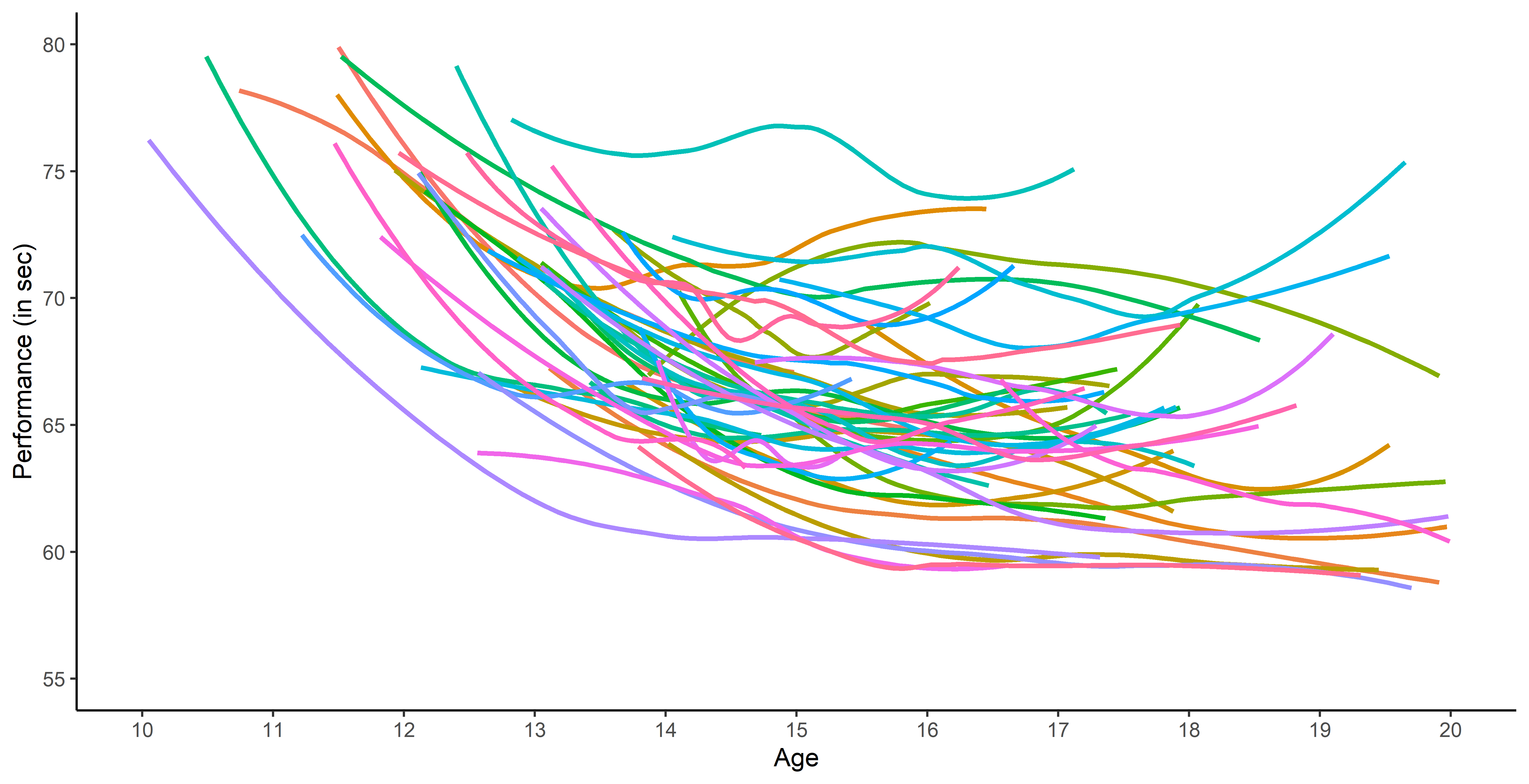
Common representation and curve clustering
A common representation as functional data is proposed by using B-splines decomposition.
Clustering curves with FunHDDC algorithm (Bouveyron & Jacques - 2011, Schmutz et al. - 2020) highlights different patterns of progression. These groups, relating both on level and trend, are consistent groups with sport experts knowledge.
Limits in terms of modelling
This approach suffers from severe limitations such as:
- unsatisfying individual modellings (side effects, sensibility to sparsity, ...),
- a lack of probabilistic prediction methods,
- persisting troubles with irregular measurements.
Contributions
Can we provide probabilistic predictions of future performances?
Gaussian process regression
No restrictions on f but a prior distribution on a functional space: f∼GP(0,C(⋅,⋅))
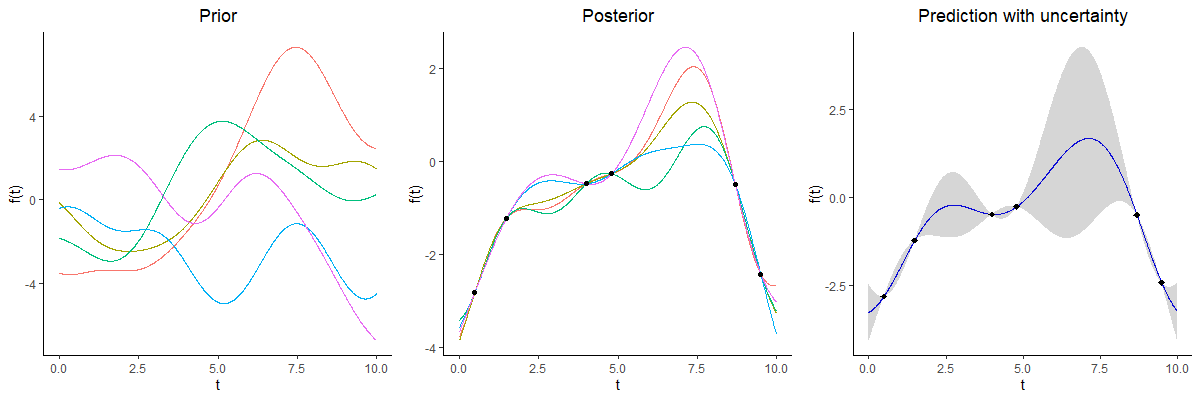
- Powerful non parametric method offering probabilistic predictions,
- Computational complexity in O(N3), with N the number of observations,
- Correspondence with infinitly wide (deep) neural networks (Neal - 1994, Lee et al. - 2018).
Modelling and prediction with a unique GP
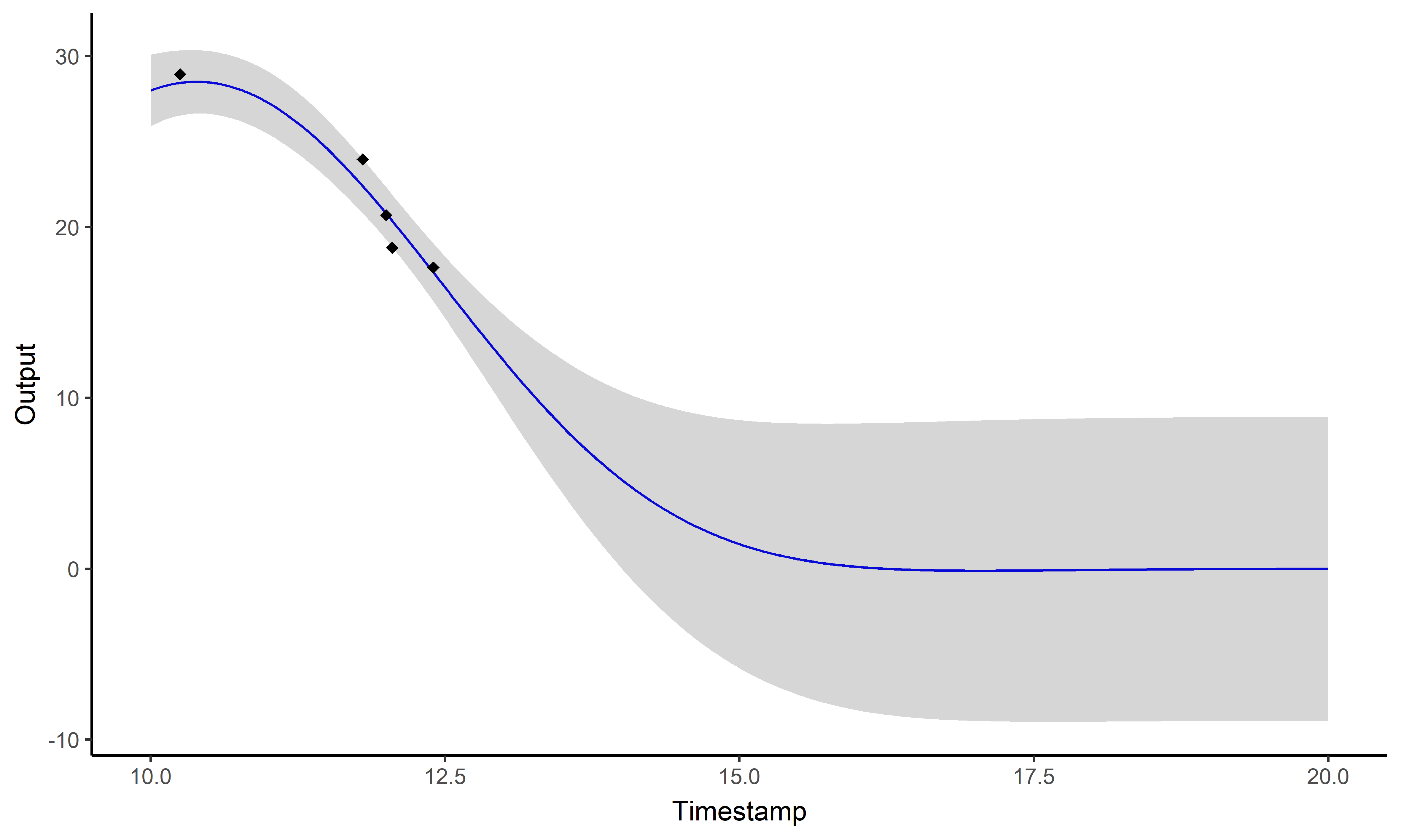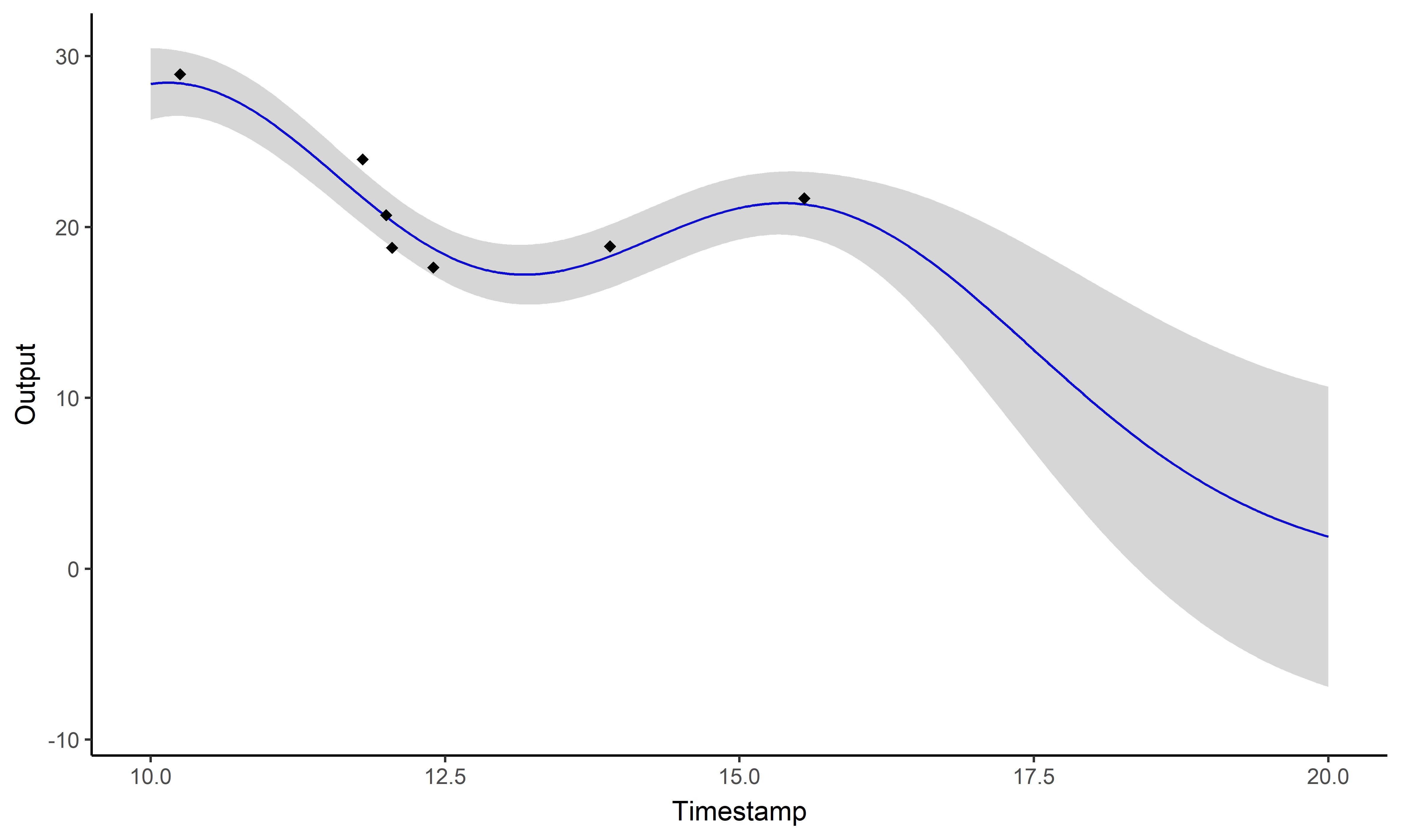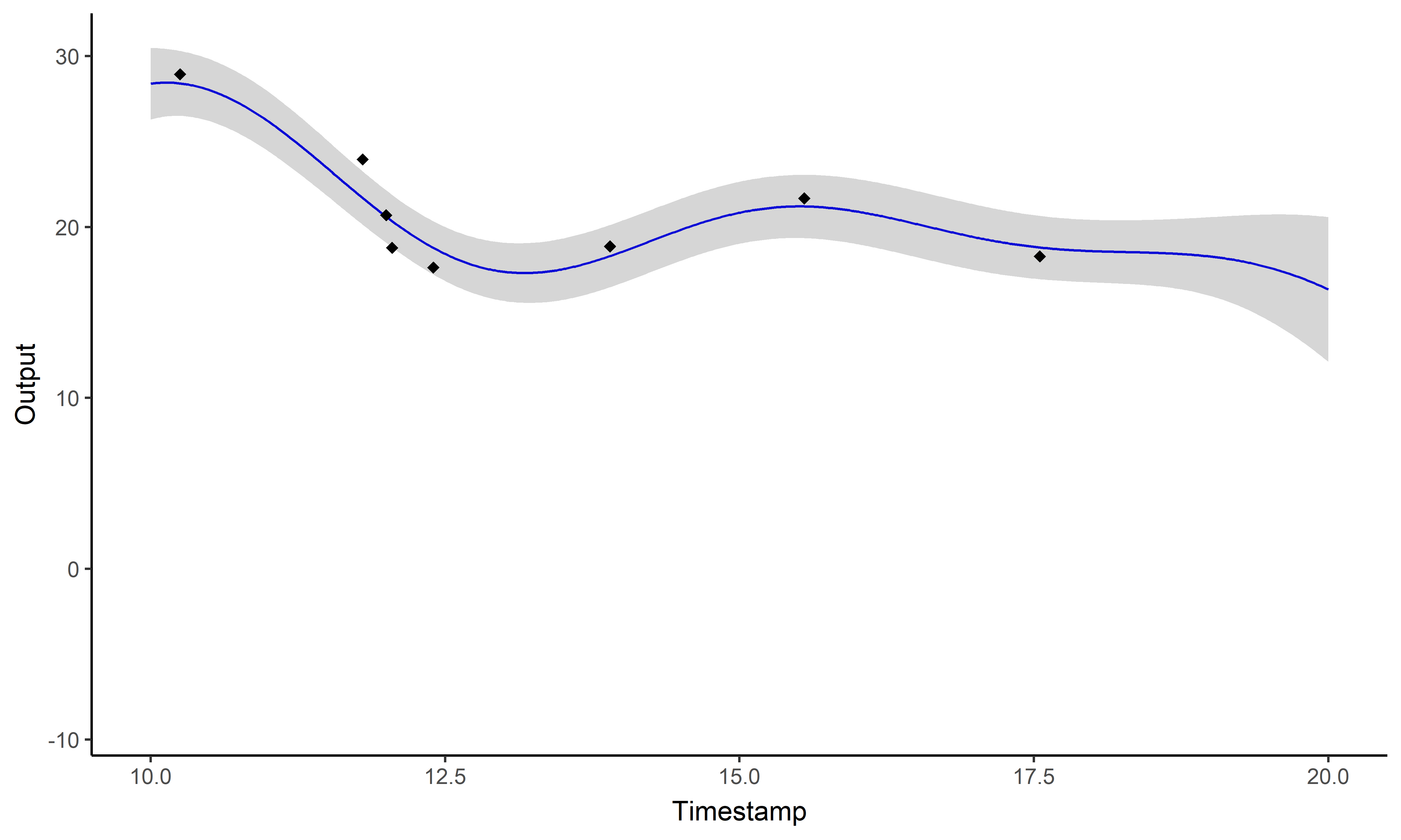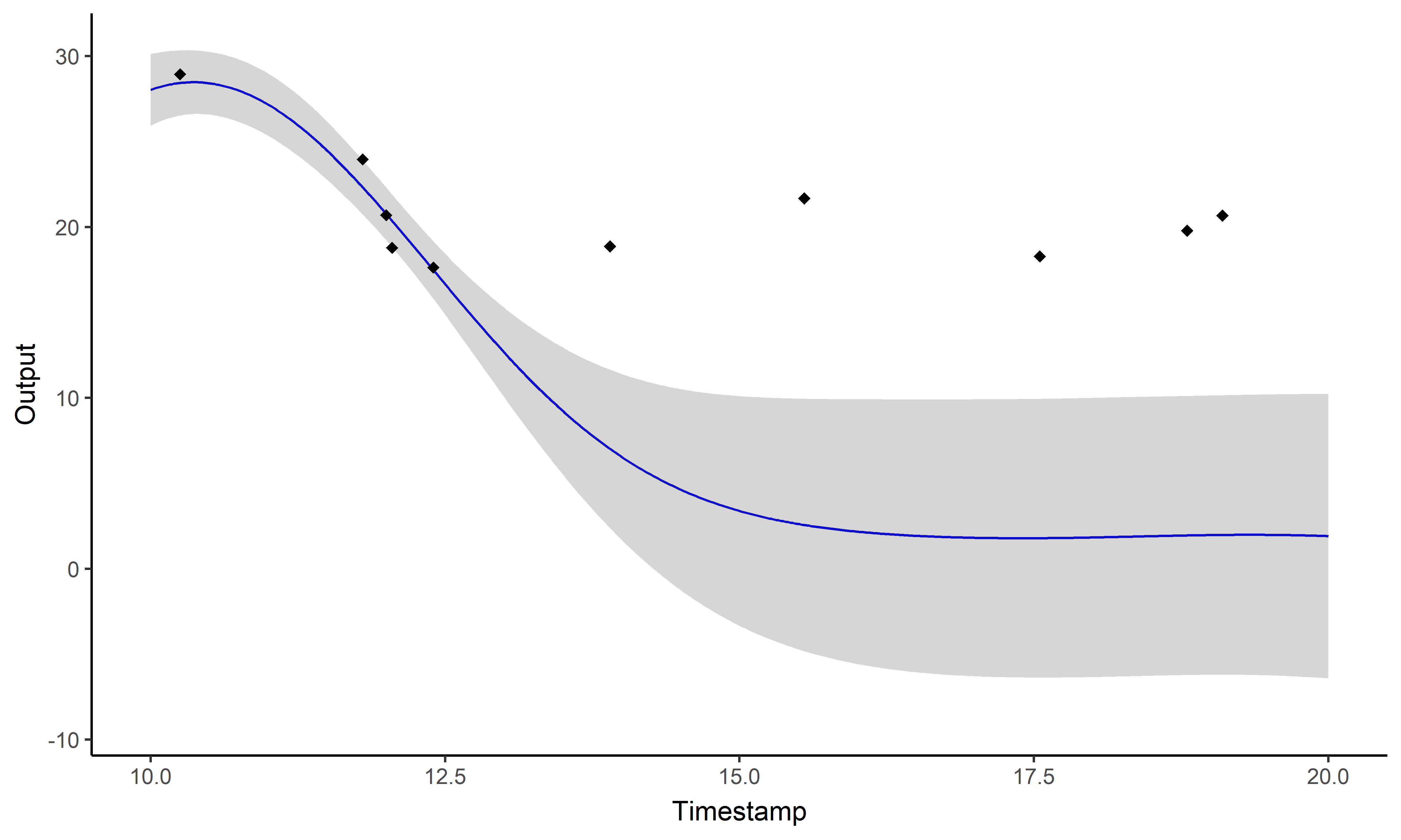
GPs provide an ideal framework for modelling although insufficient for direct predictions.
Multi-task GP with common mean (Magma)
yi=μ0+fi+ϵi
with:
- μ0∼GP(m0,Kθ0),
- fi∼GP(0,Σθi), ⊥⊥i,
- ϵi∼GP(0,σ2i), ⊥⊥i.
It follows that:
yi∣μ0∼GP(μ0,Σθi+σ2iI), ⊥⊥i
→ Unified GP framework with a common mean process μ0, and individual-specific process fi,
→ Naturaly handles irregular grids of input data.
Goal: Learn the hyper-parameters, (and μ0's hyper-posterior).
Difficulty: The likelihood depends on μ0, and individuals are not independent.
Notation and dimensionality
Each individual has its specific vector of inputs ti associated with outputs yi.
The mean process μ0 requires to define pooled vectors and additional notation follows:
- y=(y1,…,yi,…,yM)T,
- t=(t1,…,ti,…,tM)T,
- Ktθ0: covariance matrix from the process μ0 evaluated on t,
- Σtiθi: covariance matrix from the process fi evaluated on ti,
- Θ={θ0,(θi)i,σ2i}: the set of hyper-parameters,
- Ψtiθi,σ2i=Σtiθi+σ2iINi.
While GP are infinite-dimensional objects, a tractable inference on a finite set of observations fully determines the overall properties.
However, handling distributions with differing dimensions constitutes a major technical challenge.
EM algorithm: E step
Assuming to know ˆΘ, the hyper-posterior distribution of μ0 is given by: p(μ0(t)∣y,ˆΘ)∝N(μ0(t);m0(t),Ktˆθ0)×M∏i=1N(yi;μ0(ti),Ψtiˆθi,ˆσ2i)=N(μ0(t);ˆm0(t),ˆKt),
with:
- ˆK=(Ktˆθ0−1+M∑i=1˜Ψtiˆθiˆσ2i−1)−1,
- ˆm0(t)=ˆK(Ktˆθ0−1m0(t)+M∑i=1˜Ψtiˆθi,ˆσ2i−1˜yi(ti)).
EM algorithm: M step
Assuming to know p(μ0(t)∣y,ˆΘ), the estimated set of hyper-parameters is given by:
ˆΘ=argmaxΘ Eμ0[log p(y,μ0(t)∣Θ)]=logN(ˆm0(t);m0(t),Ktθ0)−12Tr(ˆKtKtθ0−1) +M∑i=1{logN(yi;ˆm0(ti),Ψtiθi,σ2)−12Tr(ˆKtiΨtiθi,σ2−1)}.
EM algorithm: M step
Assuming to know p(μ0(t)∣y,ˆΘ), the estimated set of hyper-parameters is given by:
ˆΘ=argmaxΘ Eμ0[log p(y,μ0(t)∣Θ)]=logN(ˆm0(t);m0(t),Ktθ0)−12Tr(ˆKtKtθ0−1) +M∑i=1{logN(yi;ˆm0(ti),Ψtiθi,σ2i)−12Tr(ˆKtiΨtiθi,σ2i−1)}.
- ˆm0(t) naturally acts like observed values for μ0, and ˆKt induces a variance penalty term,
- 2 or M+1 problems of numerical optimisation (analytical gradients are available).
Prediction
For a new individual, we observe some data y∗(t∗). Let us recall:
y∗∣μ0∼GP(μ0,Ψθ∗,σ2∗), ⊥⊥i
Goals:
- derive a analytical predictive distribution at arbitrary inputs tp,
- sharing the information from training individuals, stored in the mean process μ0.
Difficulties:
- the model is conditionned over μ0, a latent, unobserved quantity,
- defining the adequate target distribution is not straightforward,
- working on a new grid of inputs tp∗=(t∗,tp)⊺, potentially distinct from t.
Prediction: the key idea
Defining a multi-task prior distribution by:
- conditioning on training data,
- integrating over μ0's hyper-posterior distribution.
p(y∗(tp∗)∣y)=∫p(y∗(tp∗)∣y,μ0(tp∗))p(μ0(tp∗)∣y) dμ0(tp∗)=∫p(y∗(tp∗)∣μ0(tp∗))⏟N(y∗;μ0,Ψ∗) p(μ0(tp∗)∣y)⏟N(μ0;ˆm0,ˆK) dμ0(tp∗)=N(ˆm0(tp∗),Γ)
with:
Γ=Ψtp∗θ∗,σ2∗+ˆKtp∗
Prediction: additional steps
-
Multi-task prior:
p([y∗(t∗)y∗(tp)]∣y)=N([y∗(t∗)y∗(tp)]; [ˆm0(t∗)ˆm0(tp)],(Γ∗∗Γ∗pΓp∗Γpp))
-
Multi-task posterior:
p(y∗(tp)∣y∗(t∗),y)=N(y∗(tp); ˆμ∗(tp),ˆΓpp)
with:
- ˆμ∗(tp)=ˆm0(tp)+Γp∗Γ−1∗∗(y∗(t∗)−ˆm0(t∗))
- ˆΓpp=Γpp−Γp∗Γ−1∗∗Γ∗p
This multi-task posterior distribution provides the desired probabilistic predictions.
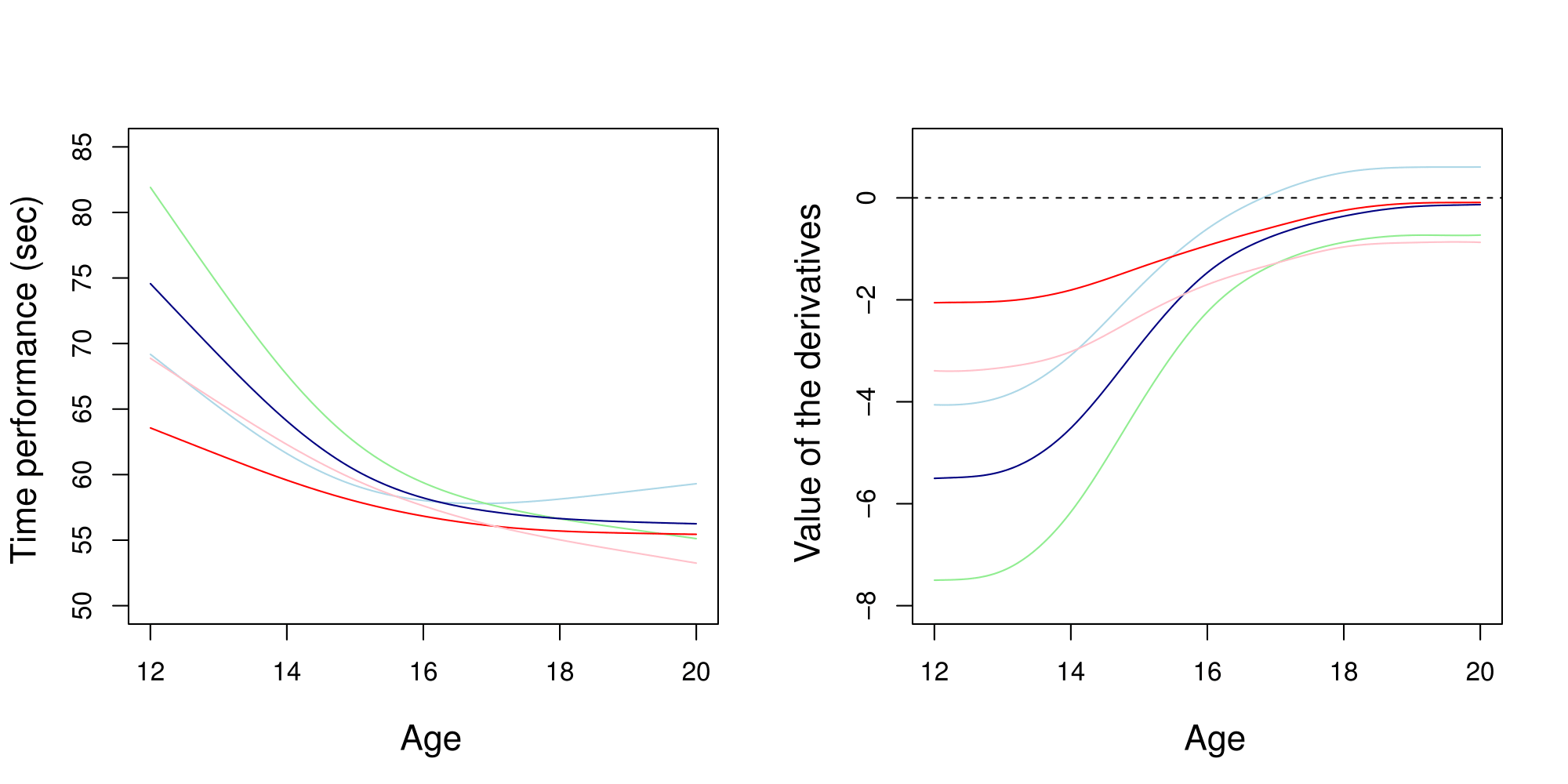
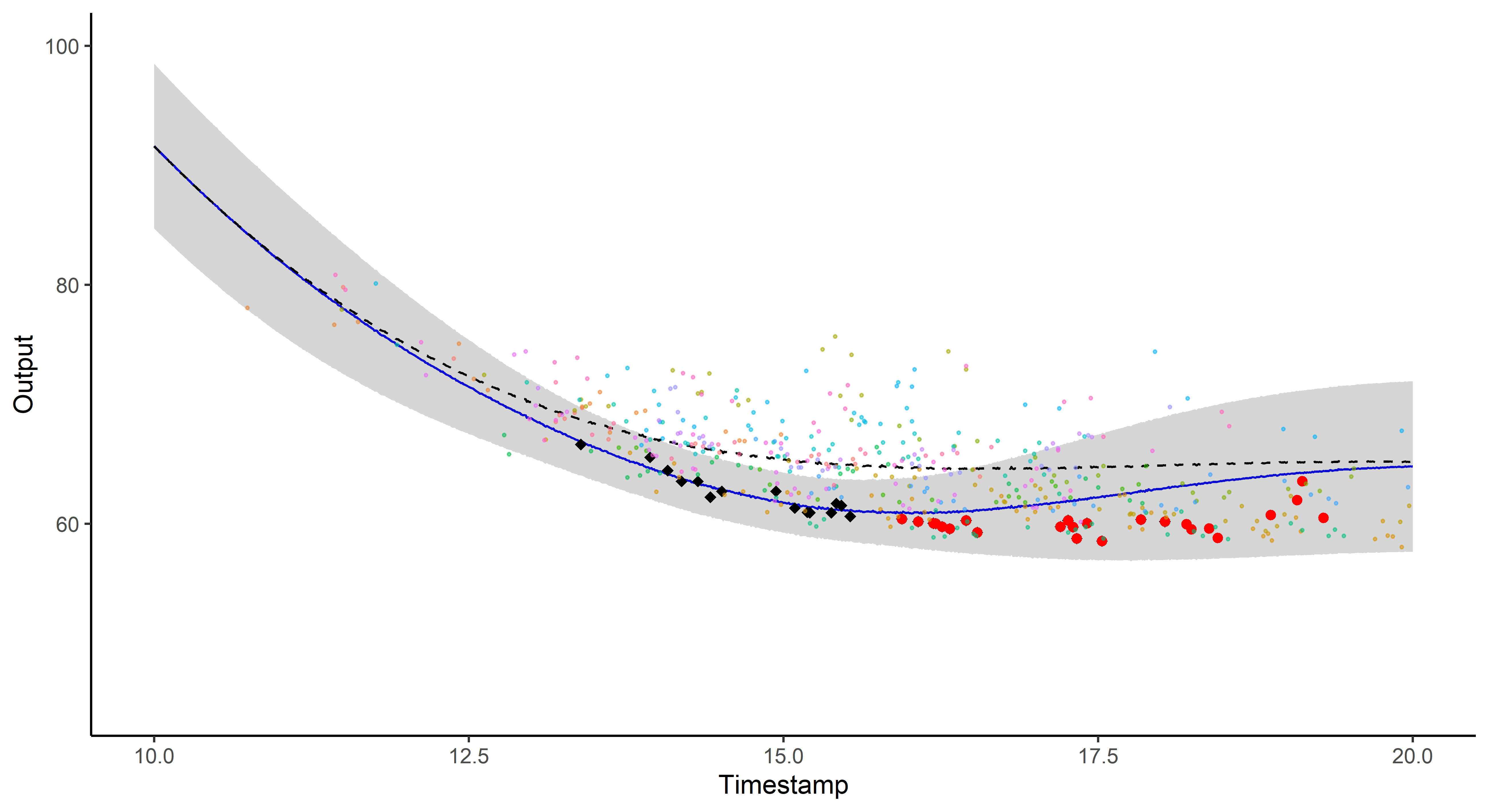
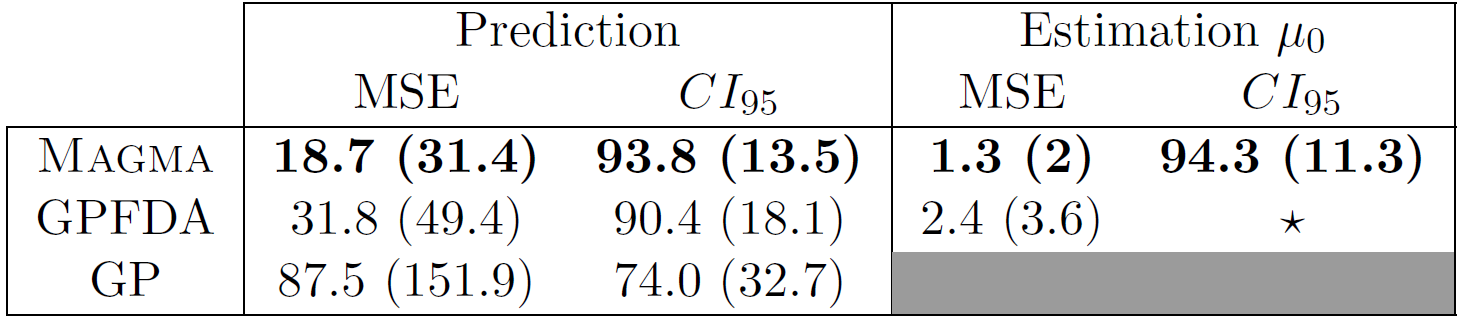
A picture is worth 1000 words
- Same data, same hyper-parameters
- Standard GP (left), Magma (right)
A GIF is worth 109 words
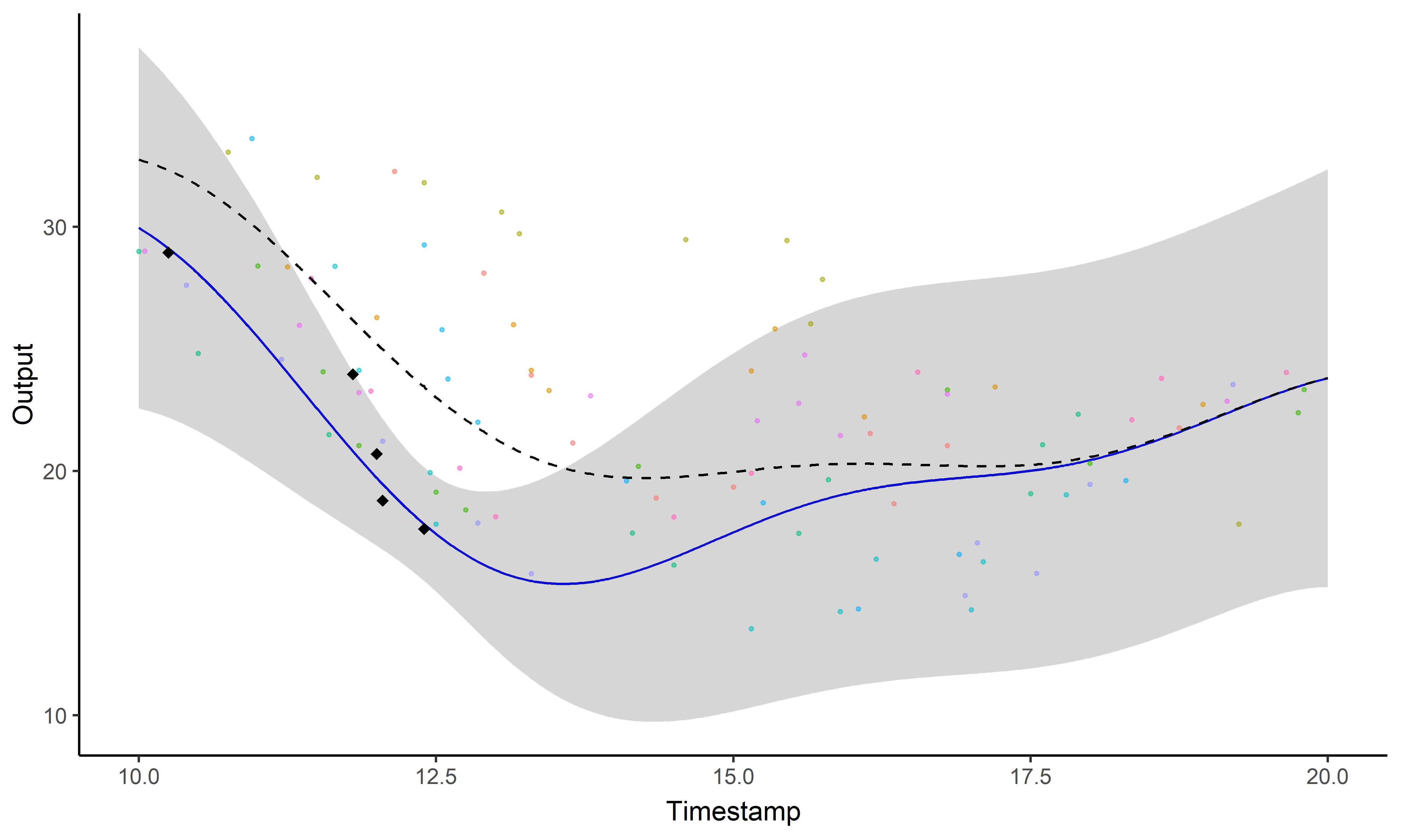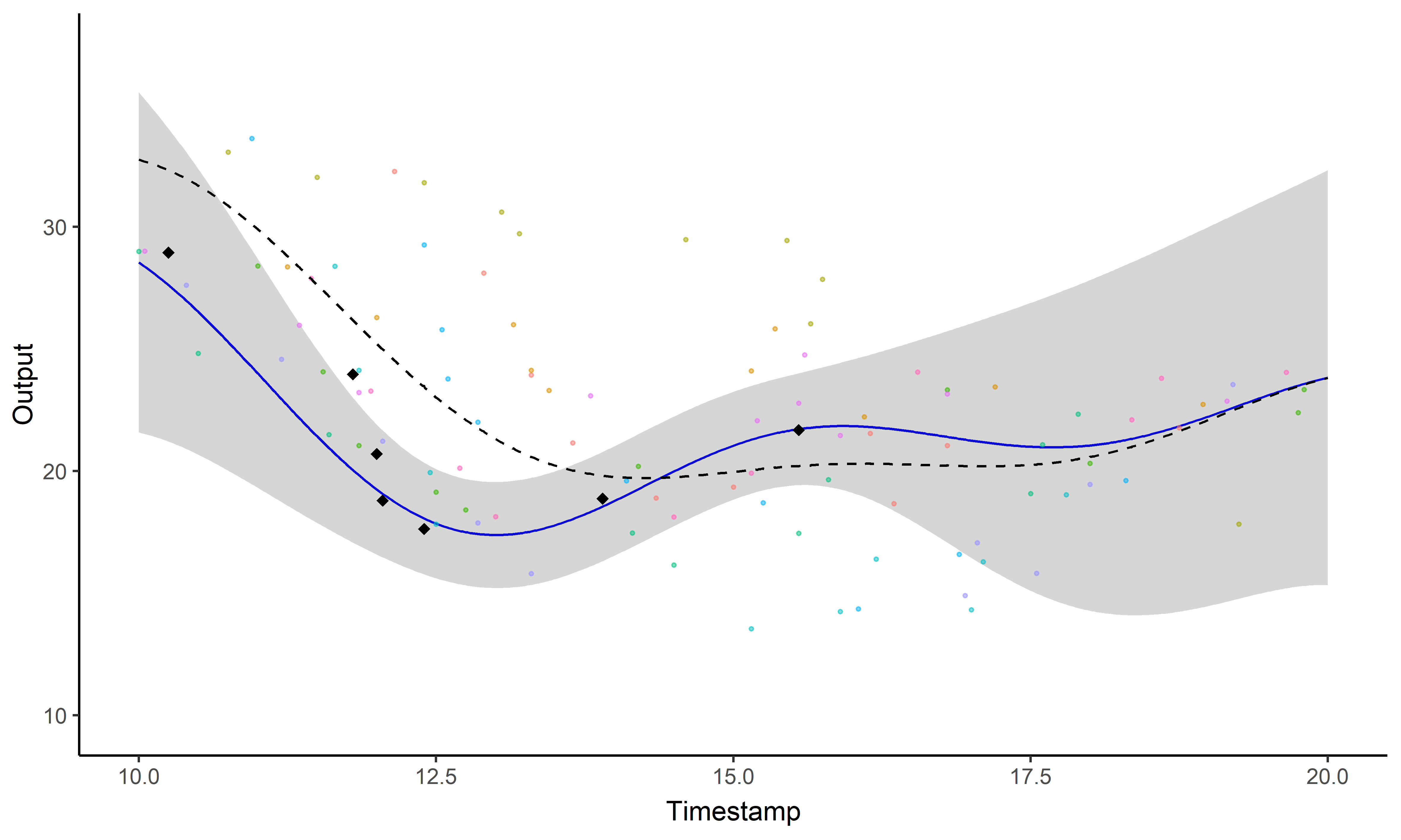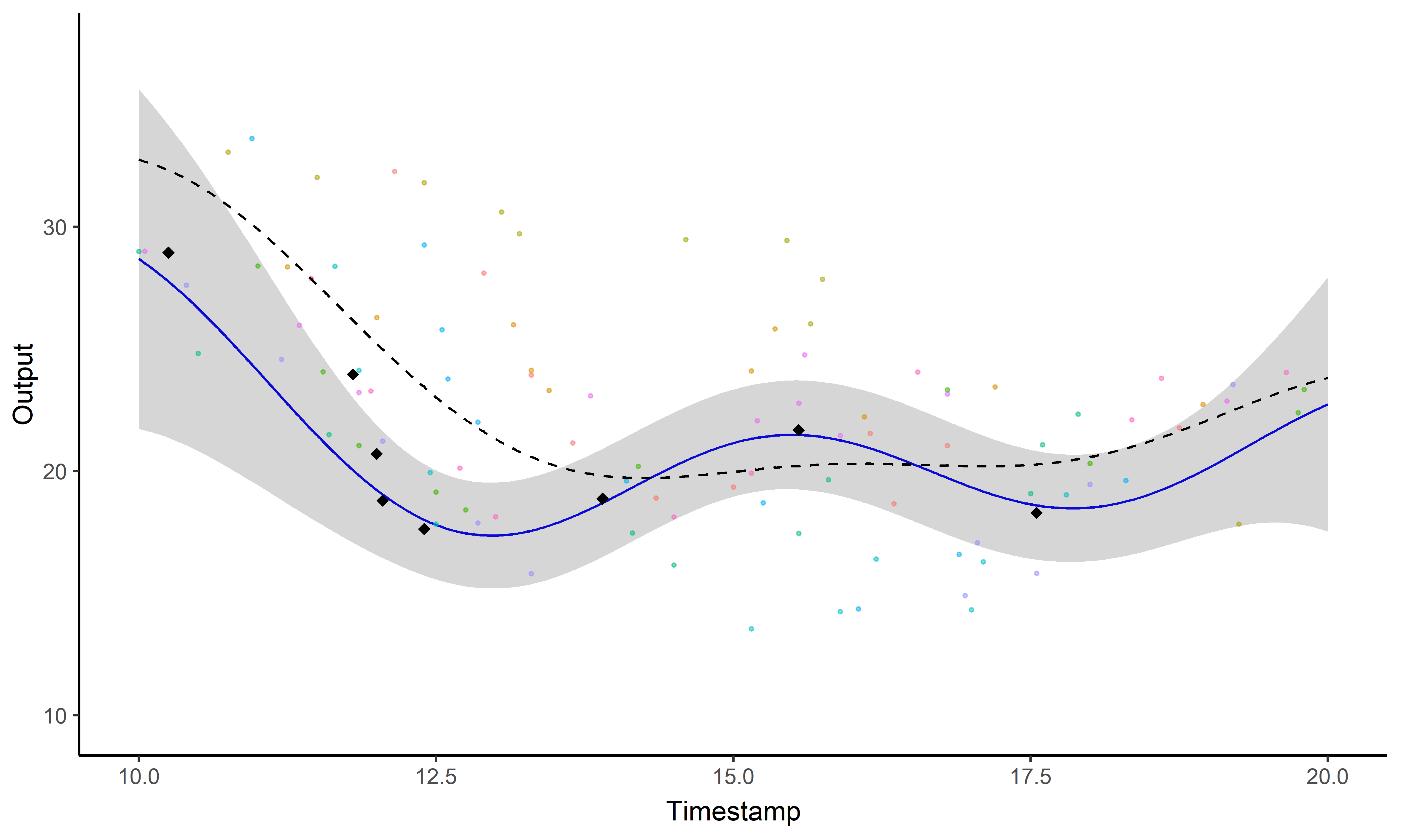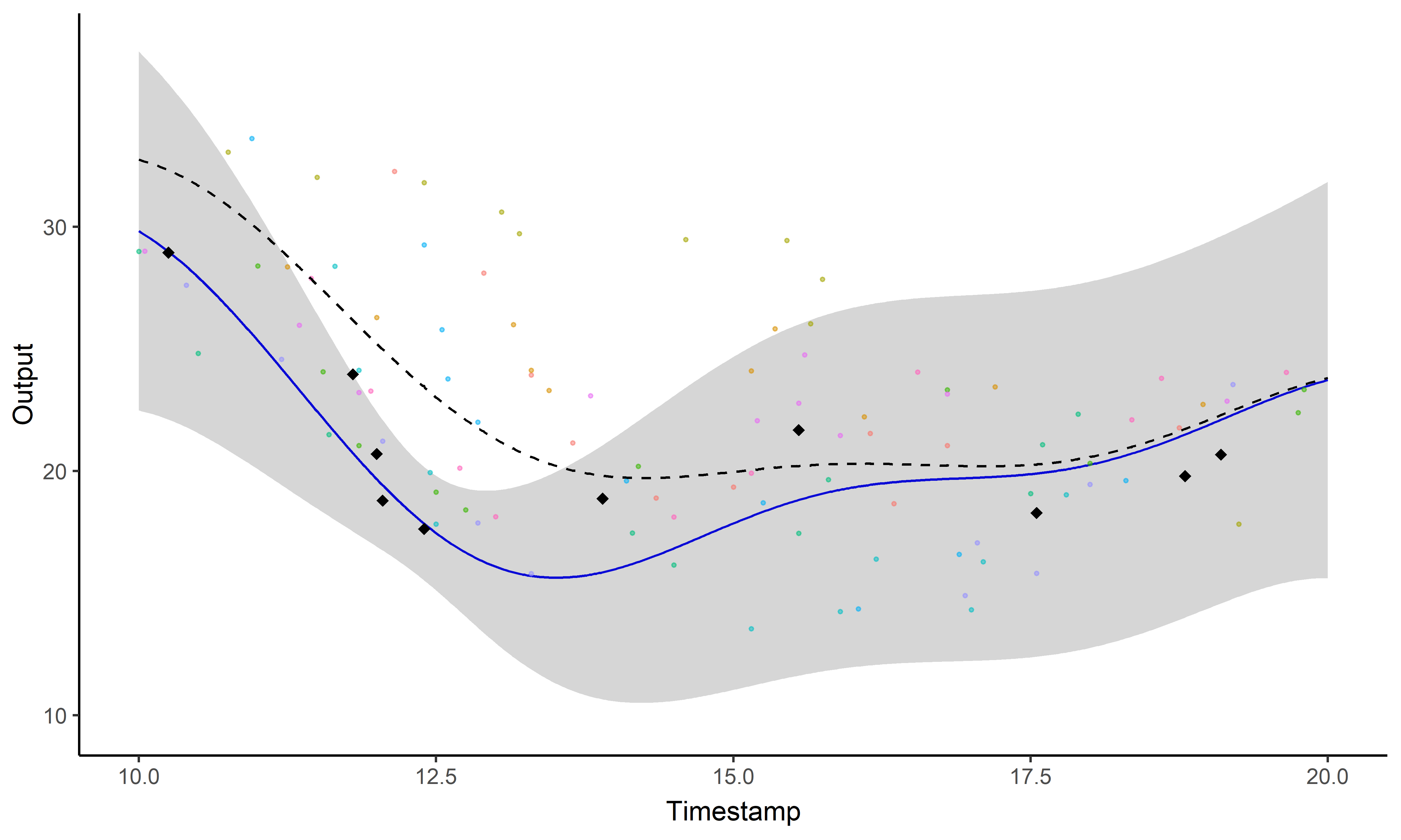
Illustration: GP regression
Contributions
May eventual group structures improve the quality of predictions?
Magma + Clustering = MagmaClust
A unique underlying mean process might be too restrictive.
→ Mixture of multi-task GPs:
yi=μ0+fi+ϵi
with:
- Zi∼M(1,π), ⊥⊥i,
- μ0∼GP(m0,Kθ0), ⊥⊥k,
- fi∼GP(0,Σθi), ⊥⊥i,
- ϵi∼GP(0,σ2i), ⊥⊥i.
It follows that:
yi∣μ0∼GP(μ0,Σθi+σ2iI), ⊥⊥i
Magma + Clustering = MagmaClust
A unique underlying mean process might be too restrictive.
→ Mixture of multi-task GPs:
yi∣{Zik=1}=μk+fi+ϵi
with:
- Zi∼M(1,π), ⊥⊥i,
- μk∼GP(mk,Cγk) ⊥⊥k,
- fi∼GP(0,Σθi), ⊥⊥i,
- ϵi∼GP(0,σ2i), ⊥⊥i.
It follows that:
yi∣μ0∼GP(μ0,Σθi+σ2iI), ⊥⊥i
Magma + Clustering = MagmaClust
A unique underlying mean process might be too restrictive.
→ Mixture of multi-task GPs:
yi∣{Zik=1}=μk+fi+ϵi
with:
- Zi∼M(1,π), ⊥⊥i,
- μk∼GP(mk,Cγk) ⊥⊥k,
- fi∼GP(0,Σθi), ⊥⊥i,
- ϵi∼GP(0,σ2i), ⊥⊥i.
It follows that:
yi∣{μ,π}∼K∑k=1πk GP(μk,Ψi), ⊥⊥i
Learning
The integrated likelihood is not tractable anymore due to posterior dependencies between μ={μk}k and Z={Zi}i.
Variational inference still allows us to maintain closed-form approximations. For any distribution q: logp(y∣Θ)=L(q;Θ)+KL(q∣∣p(μ,Z∣y,Θ))
The posterior independance is forced by an approximation assumption: q(μ,Z)=qμ(μ)qZ(Z).
Maximising the lower bound L(q;Θ) induces natural factorisations over clusters and individuals for the variational distributions.
Variational EM: E step
The optimal variational distributions are analytical and factorise such as:
ˆqμ(μ)=K∏k=1N(μk;ˆmk,ˆCk)ˆqZ(Z)=M∏i=1M(Zi;1,τi)
with:
Variational EM: M step
Optimising L(ˆq;Θ) w.r.t. Θ induces independant maximisation problems:
ˆΘ=argmaxΘEμ,Z[logp(y,μ,Z∣Θ)]=K∑k=1 N(ˆmk; mk,Cγk)−12tr(ˆCkC−1γk)+K∑k=1M∑i=1τik N(yi; ˆmk,Ψθi,σ2i)−12tr(ˆCkΨ−1θi,σ2i)+K∑k=1M∑i=1τiklogπk
Covariance structure assumption: 4 sub-models
Sharing the covariance structures offers a compromise between flexibility and parsimony:
- Hoo: common mean process - common individual process - 2 HPs,
- Hko: specific mean process - common individual process - K+1 HPs,
- Hoi: common mean process - specific individual process - M+1 HPs,
- Hki: specific mean process - specific individual process - M+K HP.
Prediction
- EM for estimating p(Z∗∣y,ˆΘ), ˆθ∗, and ˆσ2∗,
- Multi-task prior: p([y∗(t∗)y∗(tp)]∣Z∗k=1,y)=N([y∗(t∗)y∗(tp)];[ˆmk(t∗)ˆmk(tp)],(Γk∗∗Γk∗pΓkp∗Γkpp)),∀k,
-
Multi-task posterior:
p(y∗(tp)∣y∗(t∗),Z∗k=1,y)=N(ˆμk∗(tp),ˆΓkpp), ∀k,
-
Predictive multi-task GPs mixture:
p(y∗(tp)∣y∗(t∗),y)=K∑k=1τ∗k N(ˆμk∗(tp),ˆΓkpp(tp)).
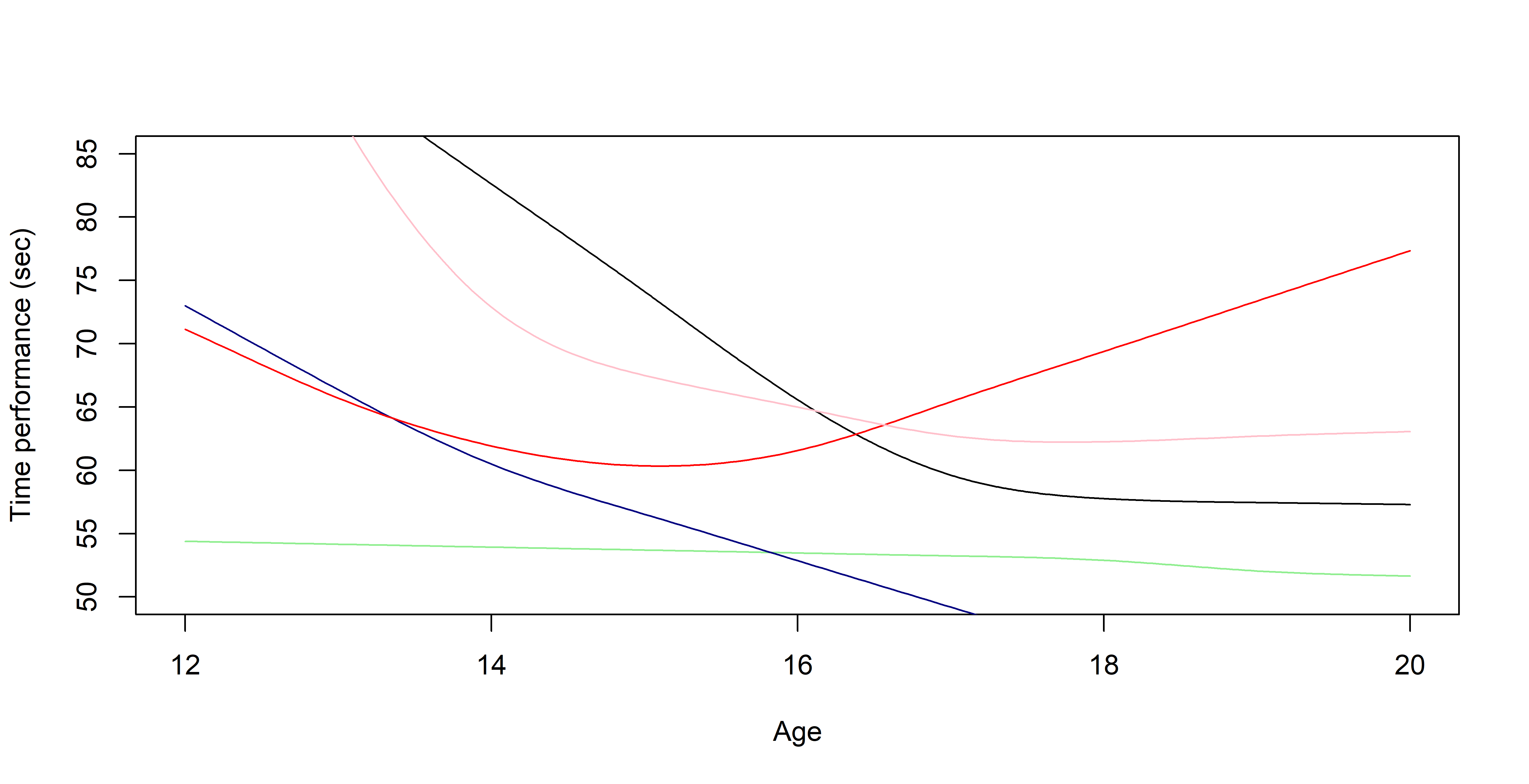
Illustration: Magma vs MagmaClust
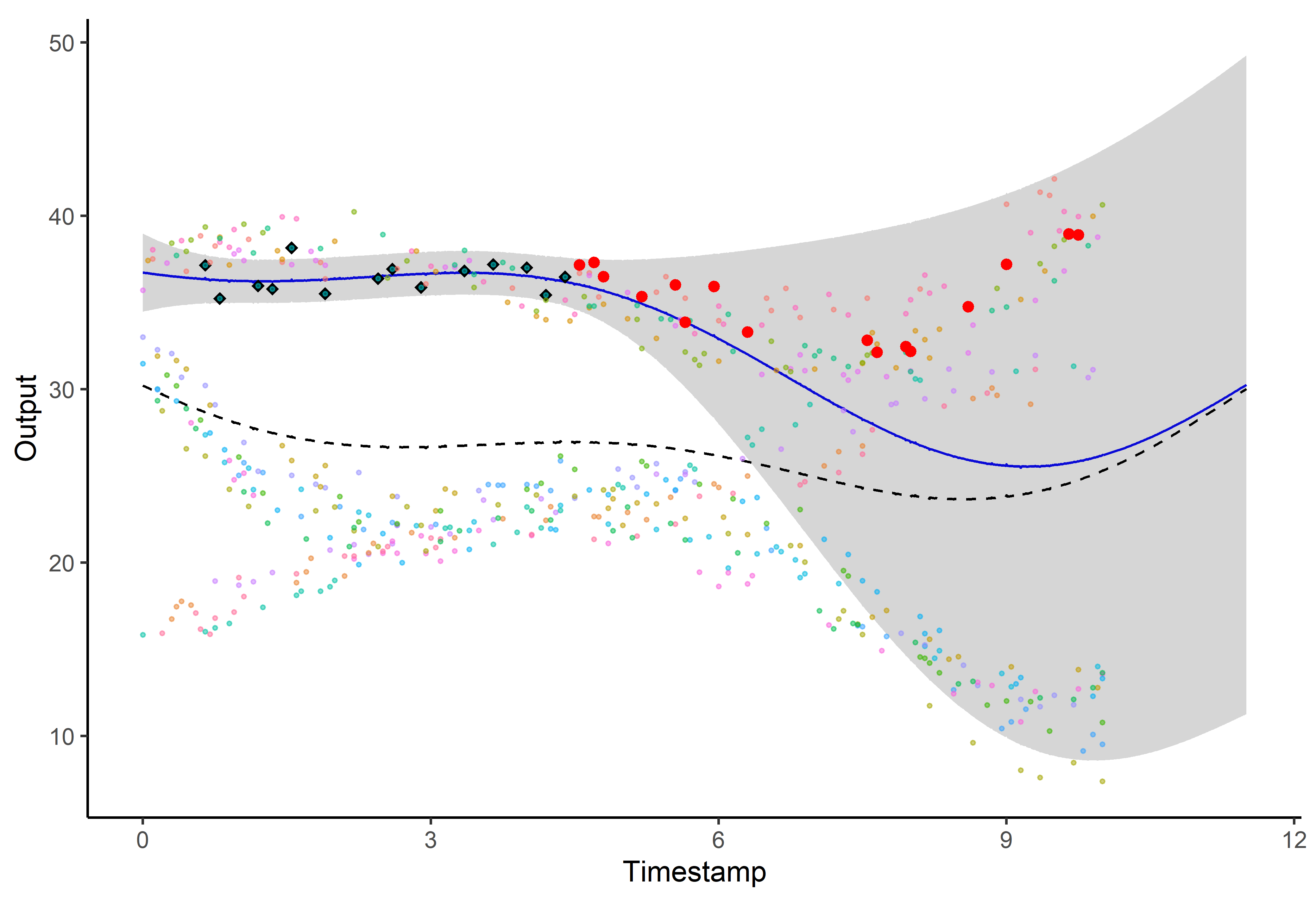
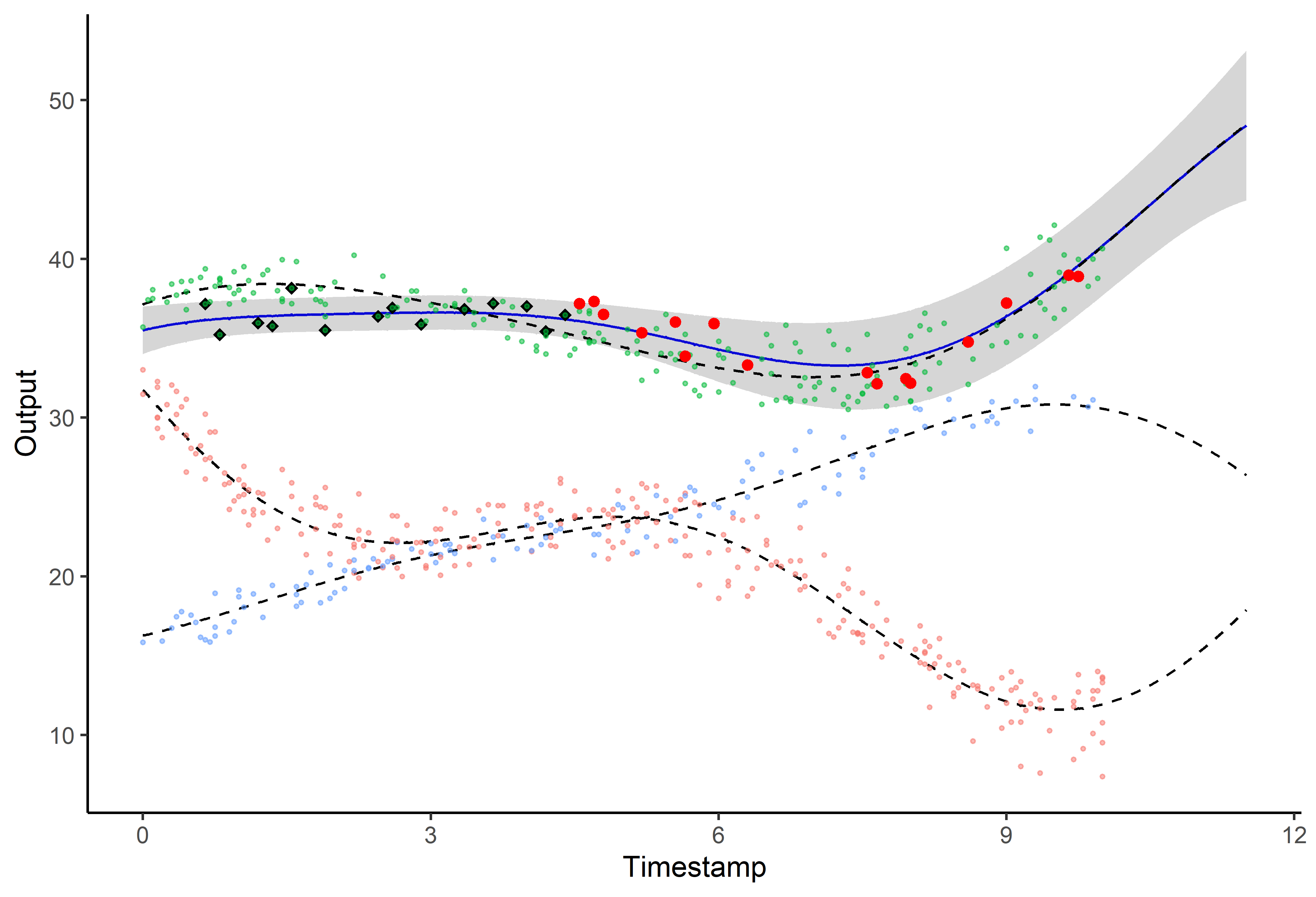
Clustering performances
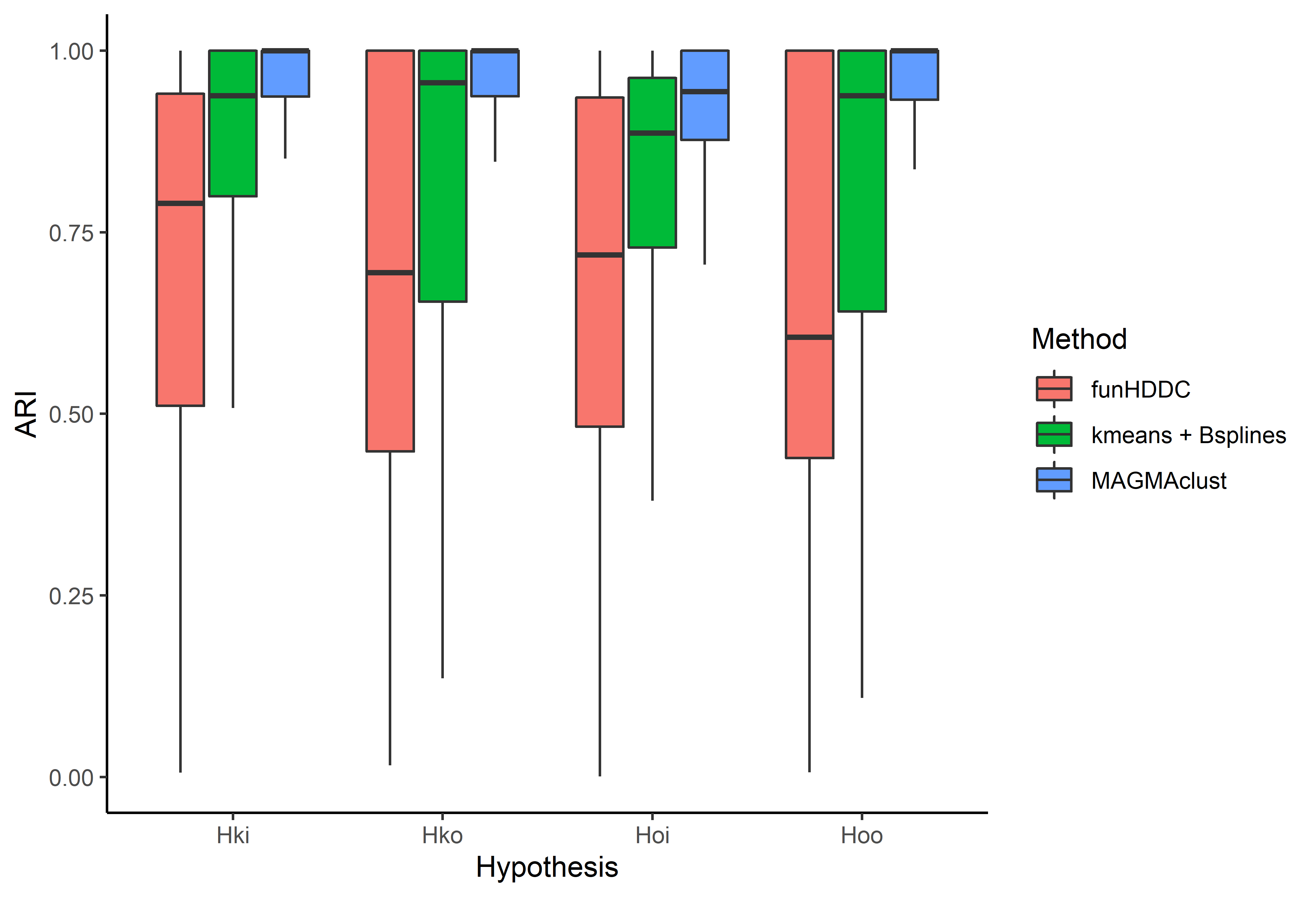
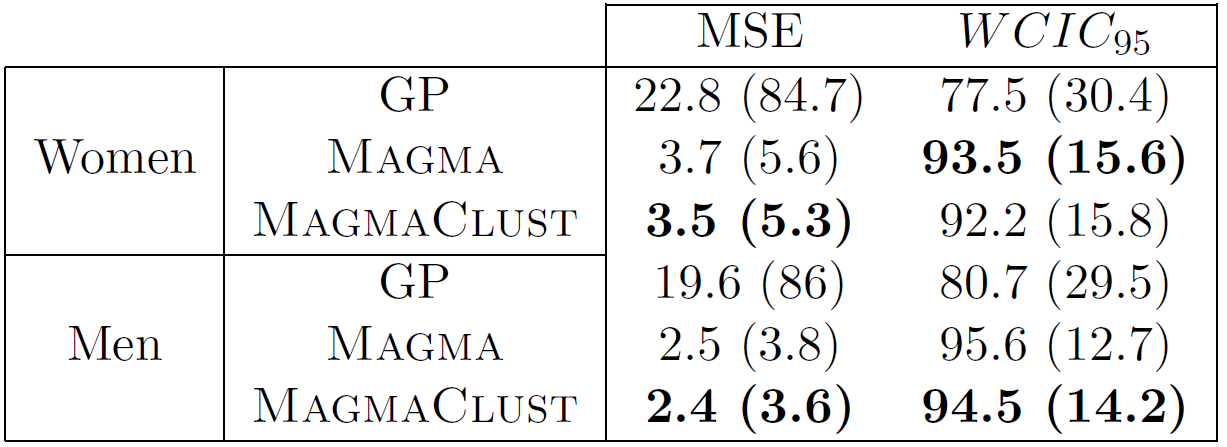
Predictive performances on swimmers datasets

And what about the swimmers ?
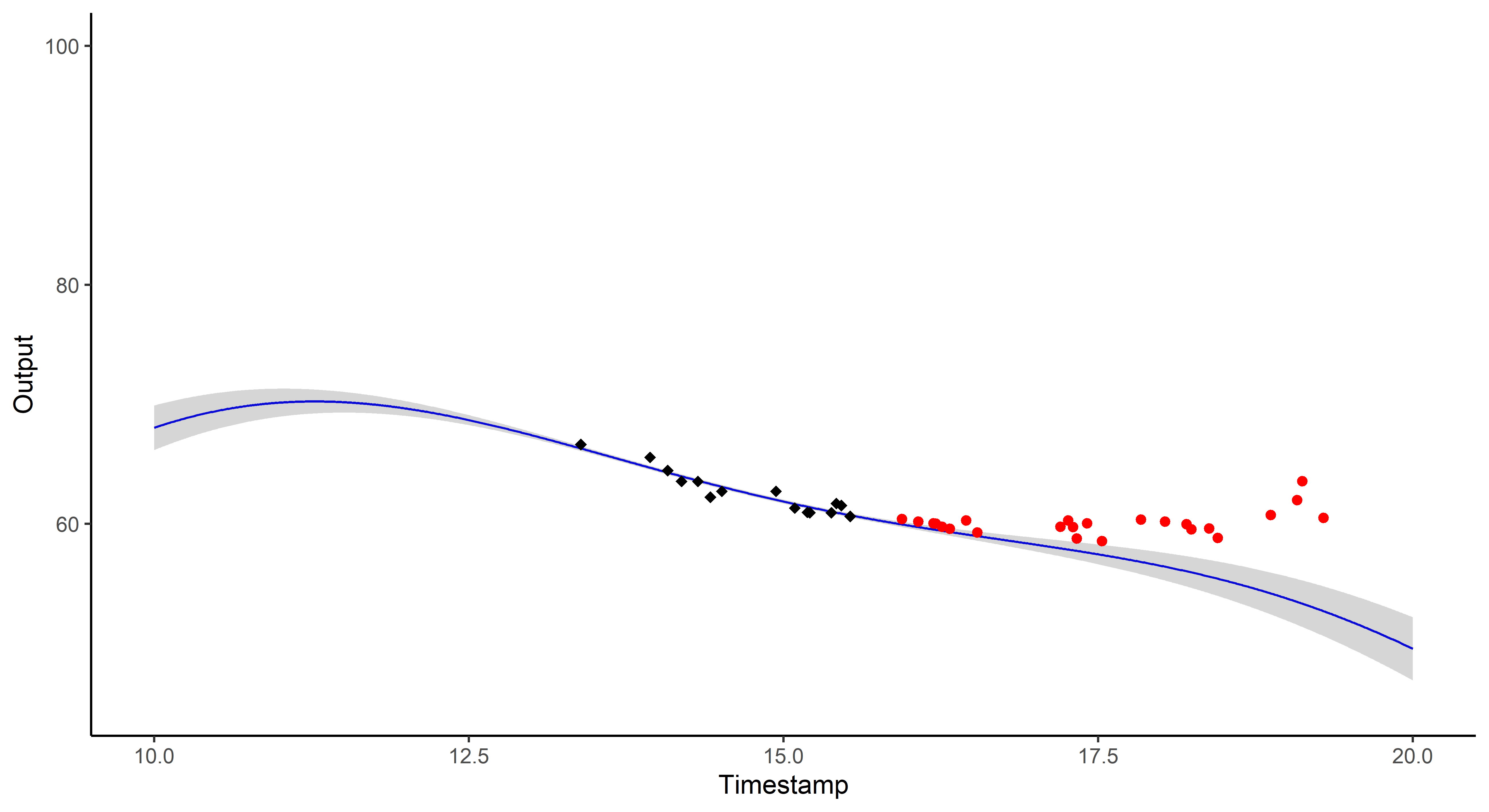
And what about the swimmers ?

And what about the swimmers ?
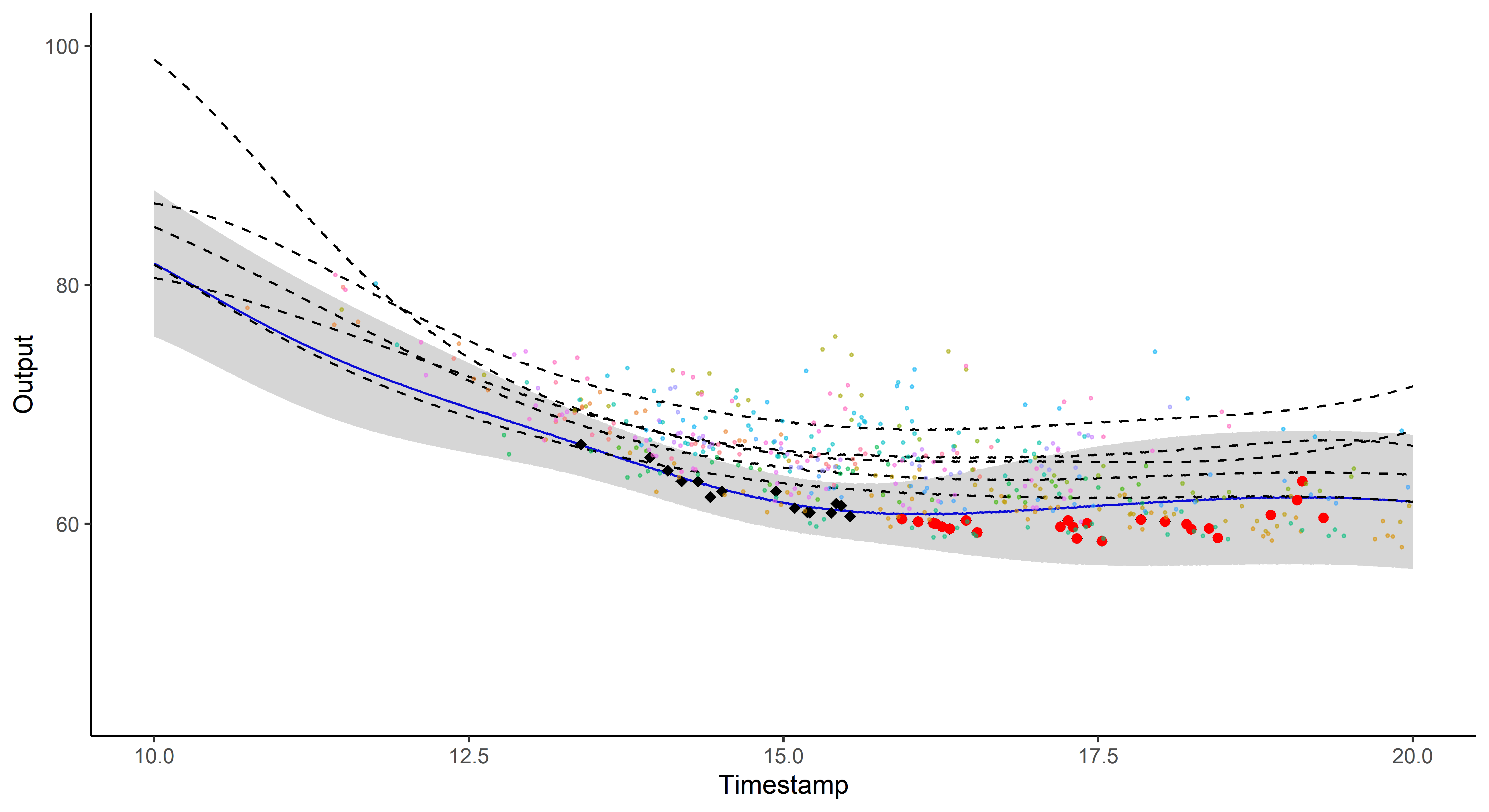
Predictive performances on swimmers datasets
Did I mention that I like GIFs ?
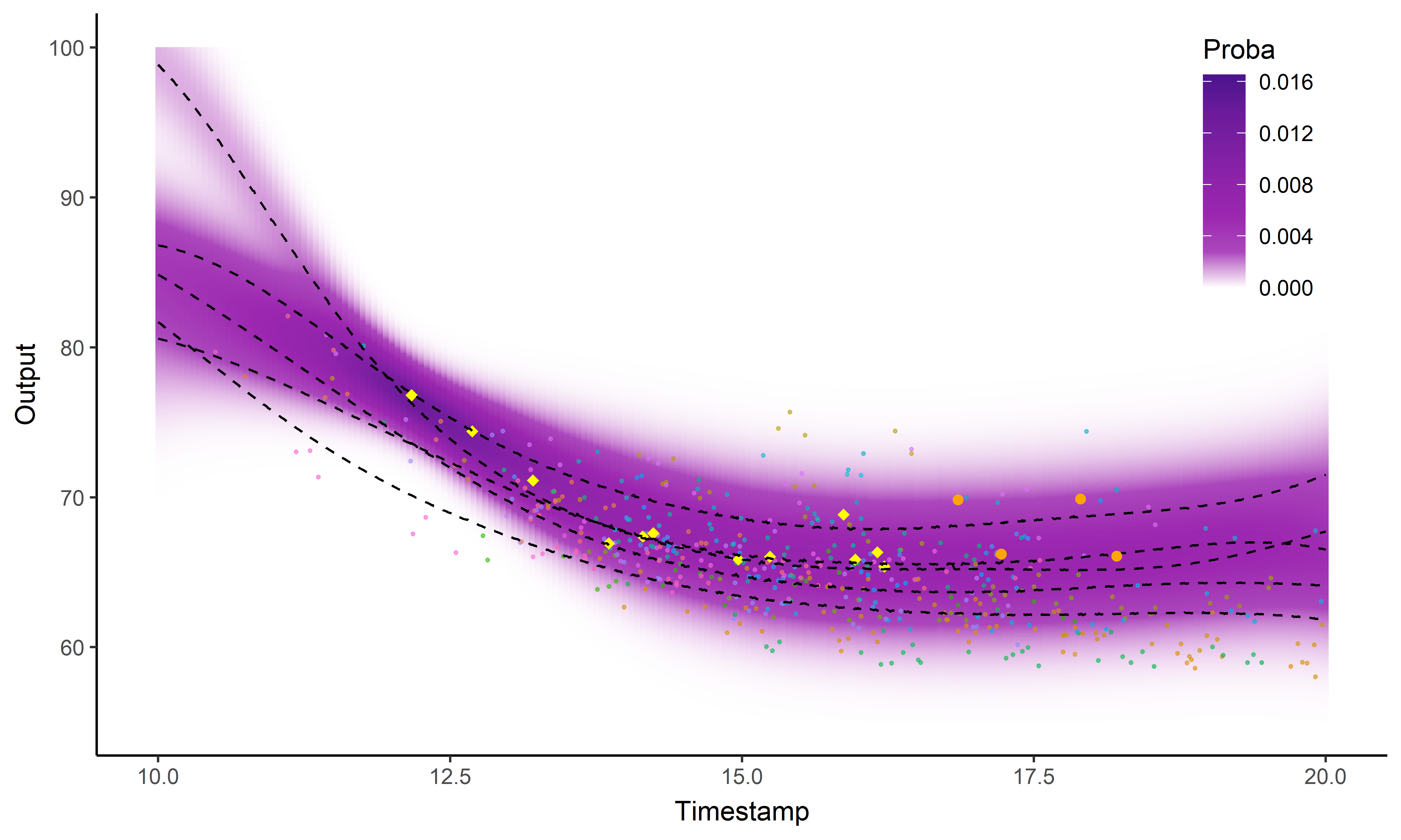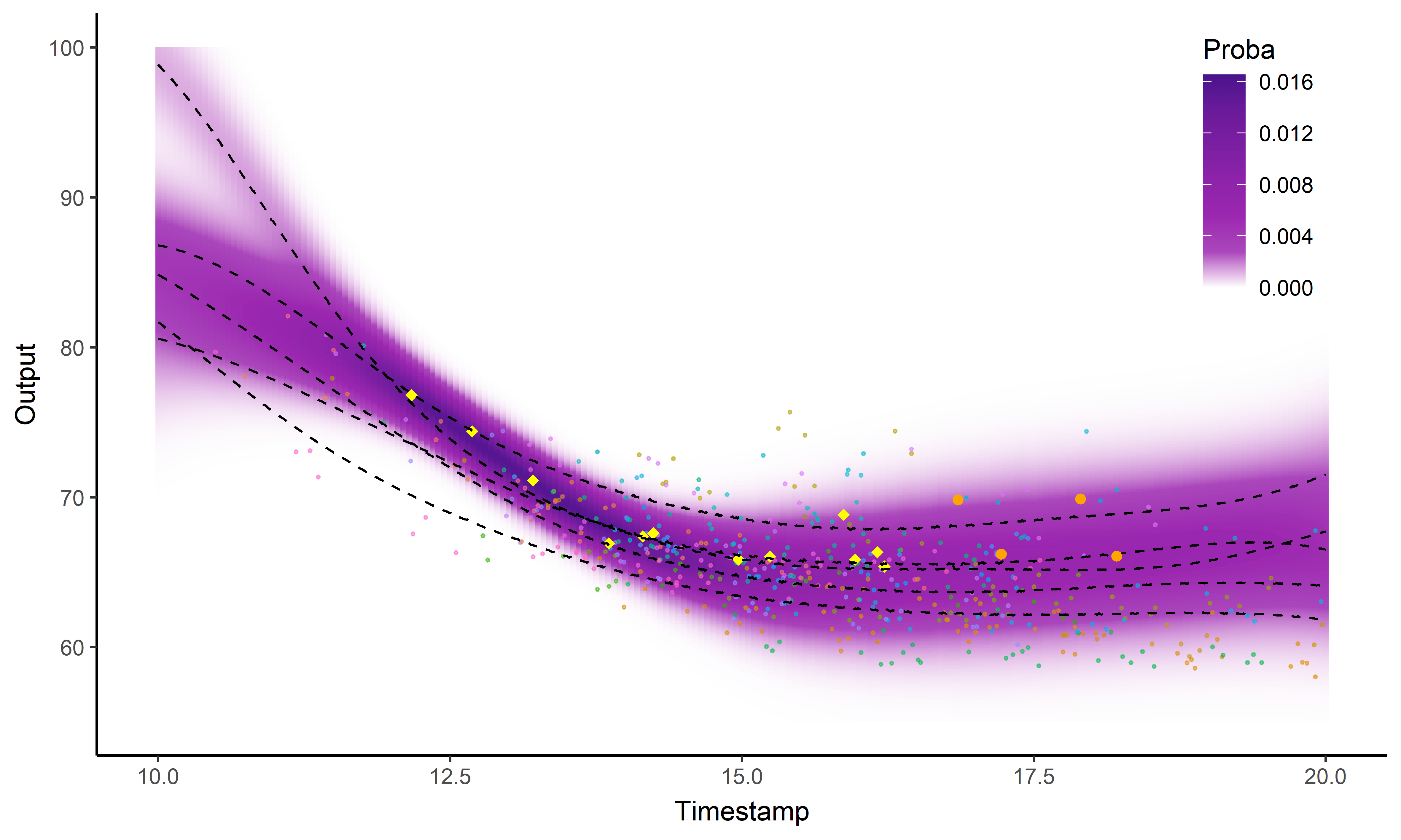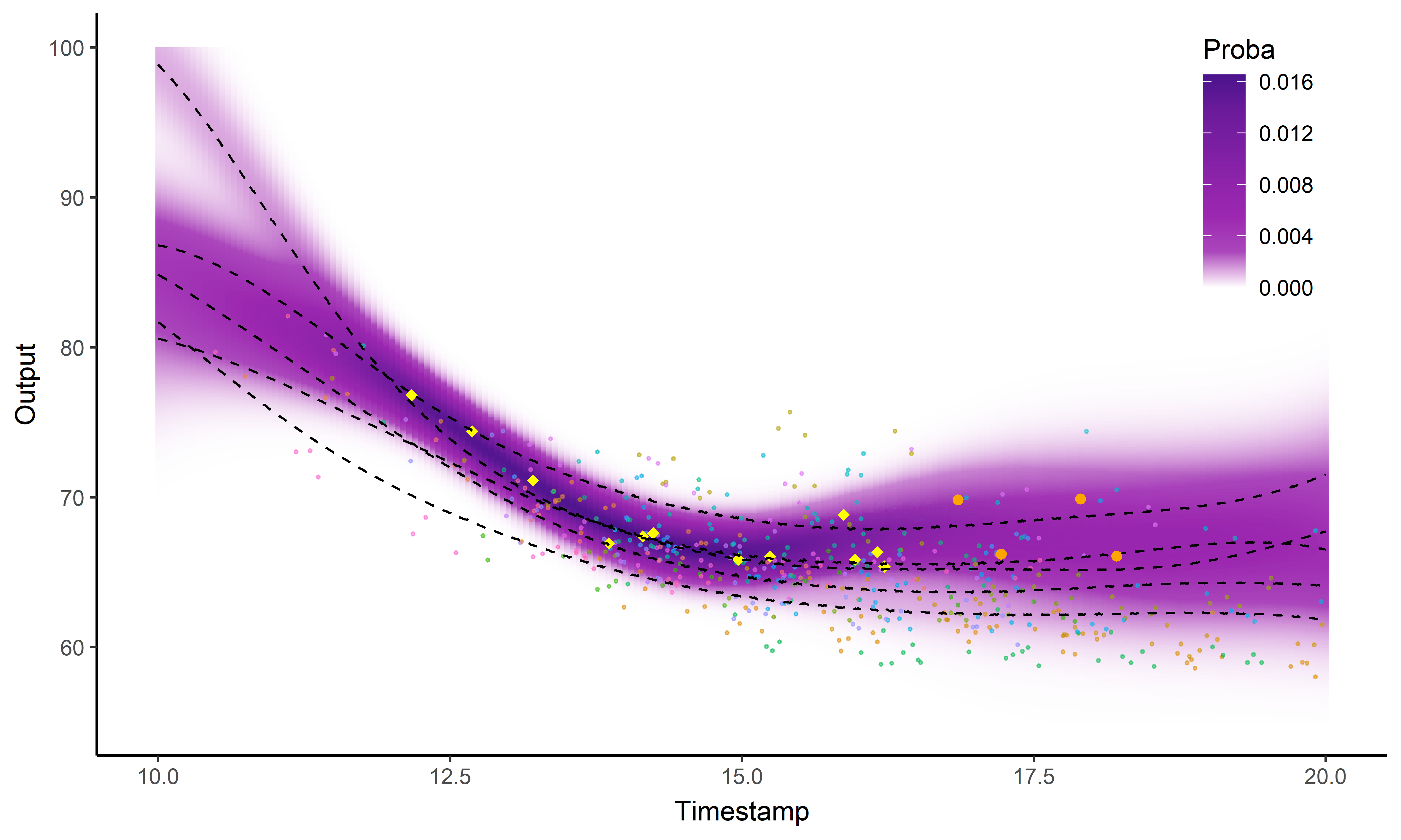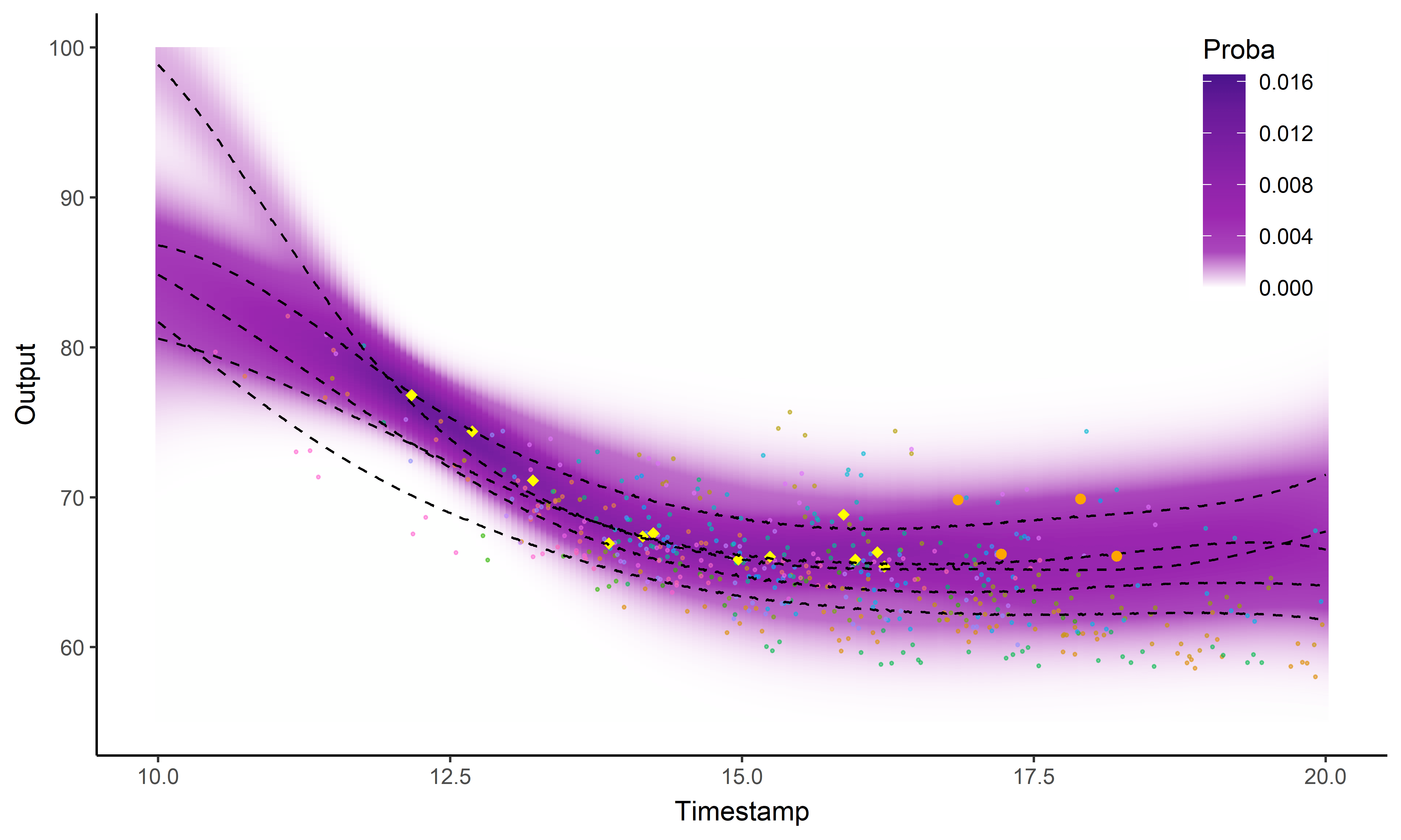
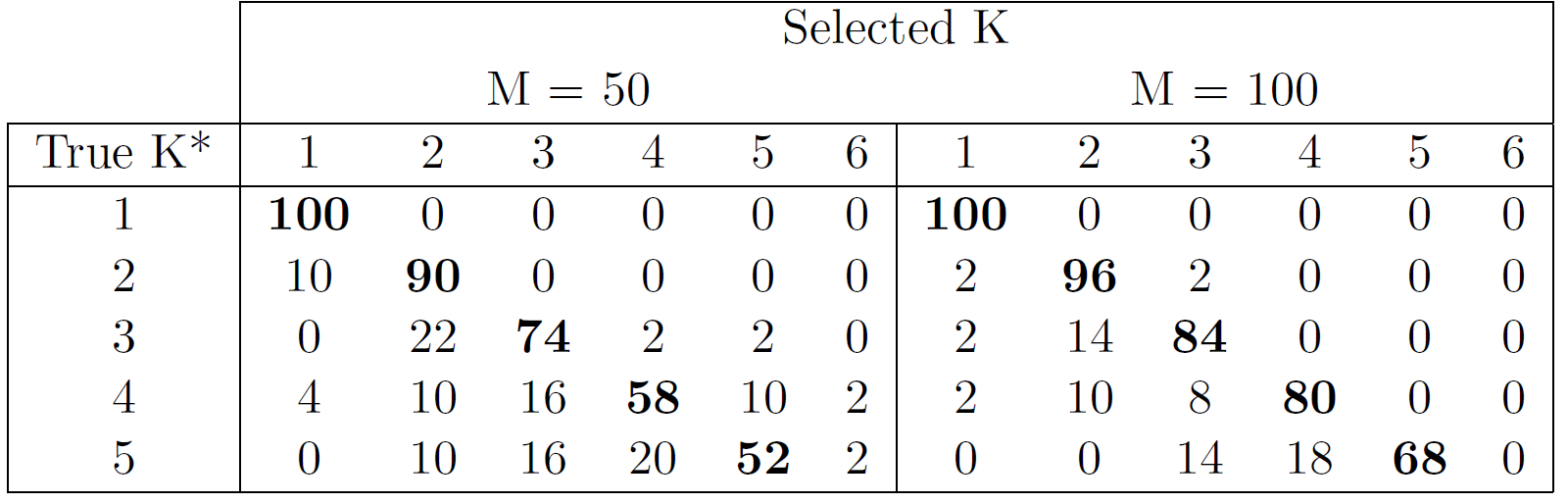
Perspectives: model selection in MagmaClust
Leroy & al. - 2020 - preprint
After convergence of the VEM algorithm, a variational-BIC expression can be derived as:
Perspectives
-
Enable association with sparse GP approximations, -
Extend to multivariate functional regression, -
Develop an online version, -
Integrate to the FFN app and launch real-life tests, -
Investigate GP variational encoder for functional data
References
- Neal - Priors for infinite networks - University of Toronto - 1994
- Shi and Wang - Curve prediction and clustering with mixtures of Gaussian process functional regression models - Statistics and Computing - 2008
- Bouveyron and Jacques - Model-based clustering of time series in group-specific functional subspaces - Advances in Data Analysis and Classification - 2011
- Boccia et al. - Career Performance Trajectories in Track and Field Jumping Events from Youth to Senior Success: The Importance of Learning and Development - PLoS ONE - 2017
- Lee et al. - Deep Neural Networks as Gaussian Processes - ICLR - 2018
- Kearney et Hayes - Excelling at youth level in competitive track and field athletics is not a prerequisite for later success - Journal of Sports Sciences - 2018
- Leroy et al. - Functional Data Analysis in Sport Science: Example of Swimmers’ Progression Curves Clustering - Applied Sciences - 2018
- Schmutz et al. - Clustering multivariate functional data in group-specific functional subspaces - Computational Statistics - 2020
- Leroy et al. - Magma: Inference and Prediction with Multi-Task Gaussian Processes - Under review - 2020
- Leroy et al. - Cluster-Specific Predictions with Multi-Task Gaussian Processes - Under review - 2020
Annexe
Two important prediction steps of Magma have been omitted for clarity:
- Recomputing the hyper-posterior distribution on the new grid: p(μ0(tp∗)∣y),
- Estimating the hyper-parameters of the new individual: ˆθ∗,ˆσ2∗=argmaxθ∗,σ2∗ p(y∗(t∗)∣y,θ∗,σ2∗).
The computational complexity for learning is given by:
- Magma: O(M×N3i+N3)
- MagmaClust: O(M×N3i+K×N3)
Annexe: MagmaClust, remaining clusters
Annexe: model selection performances of VBIC