Talent detection in sport:
Machine Learning methods for performance prediction

Context

Traditional talent identification:
\(\rightarrow\) Best young athlete + coach intuition

G. Boccia et al. (2017) :

\(\simeq\) 60% of 16 years old elite athletes do not maintain their level of performance

Philip E. Kearney & Philip R. Hayes (2018) :

\(\simeq\) only 10% of senior top 20 were also top 20 before 13 years

Data

Performances from FF of Swimming members since 2002:

• Irregular time series
• Different number \(N_i\) of observations between individuals
• Different observational timestamps \(t_i^k\)
• \(N_i\) \(\simeq x \times10^1\)

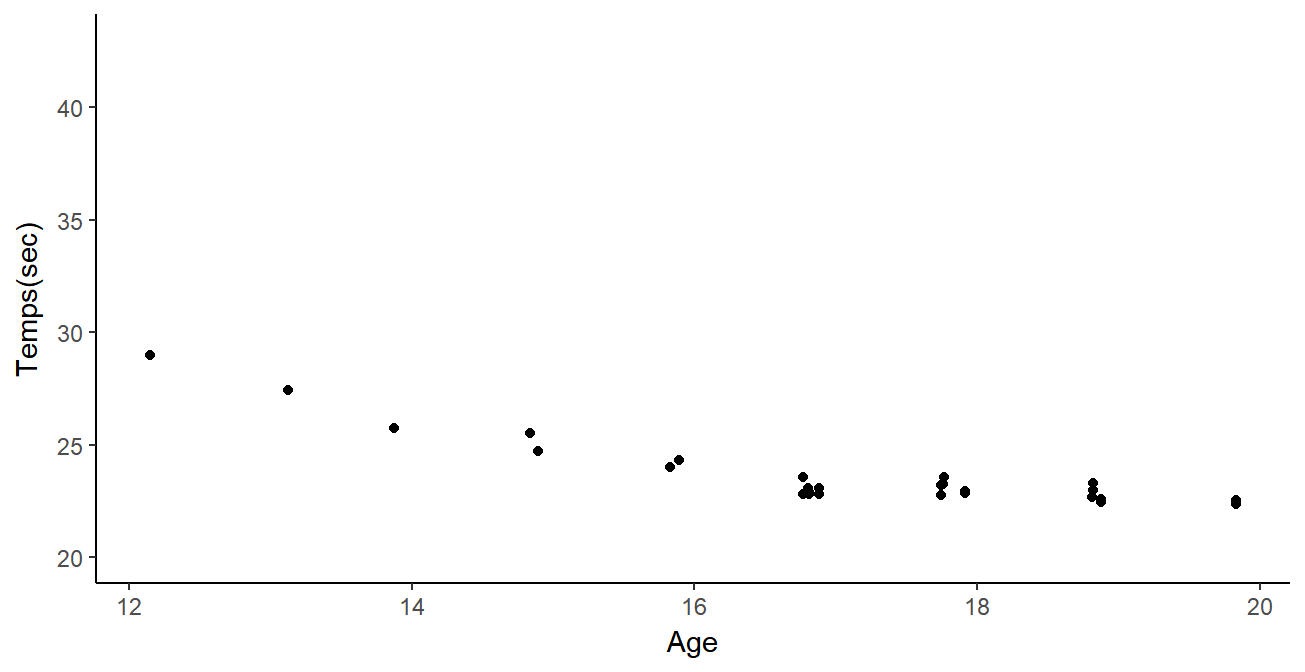
Data

Performances from FF of Swimming members since 2002:

• Irregular time series
• Different number \(N_i\) of observations between individuals
• Different observational timestamps \(t_i^k\)
• \(N_i\) \(\simeq x \times10^1\) | \(N\) \(= \sum\limits_{i=1}^{M}\) \(N_i\) \(\simeq x \times 10^5\)

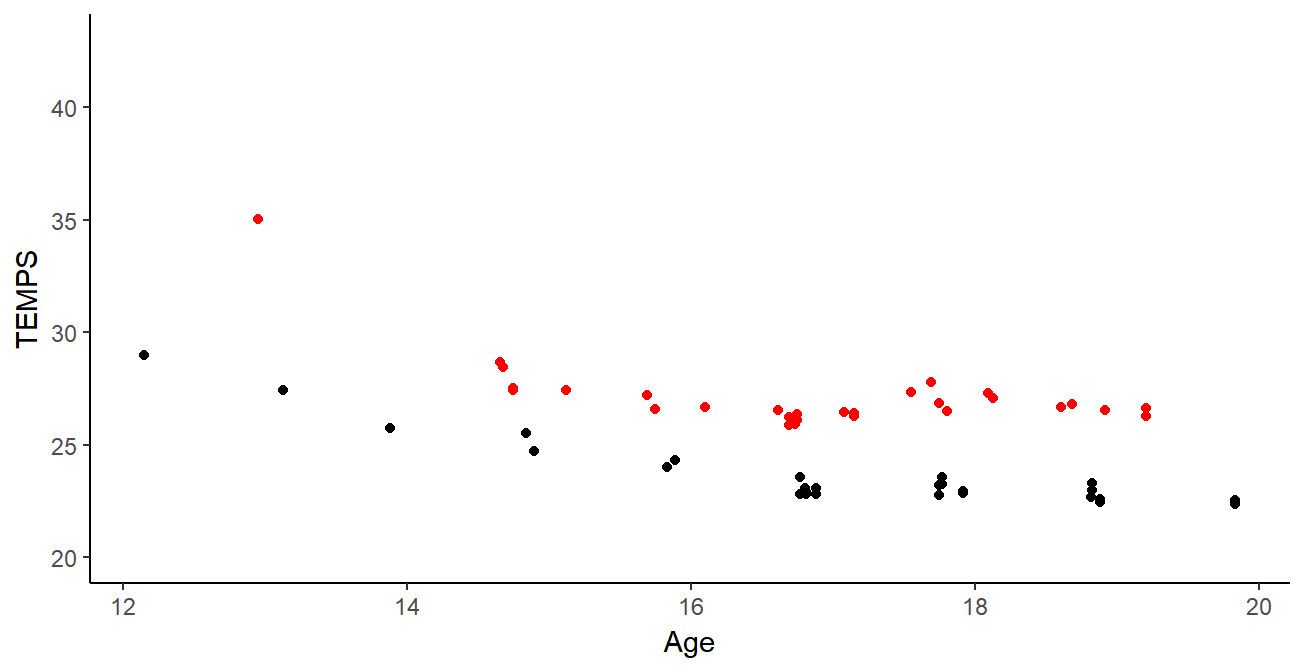
Data

Performances from FF of Swimming members since 2002:

• Irregular time series
• Different number \(N_i\) of observations between individuals
• Different observational timestamps \(t_i^k\)
• \(N_i\) \(\simeq x \times10^1\) | \(N\) \(= \sum\limits_{i=1}^{M}\) \(N_i\) \(\simeq x \times 10^5\)

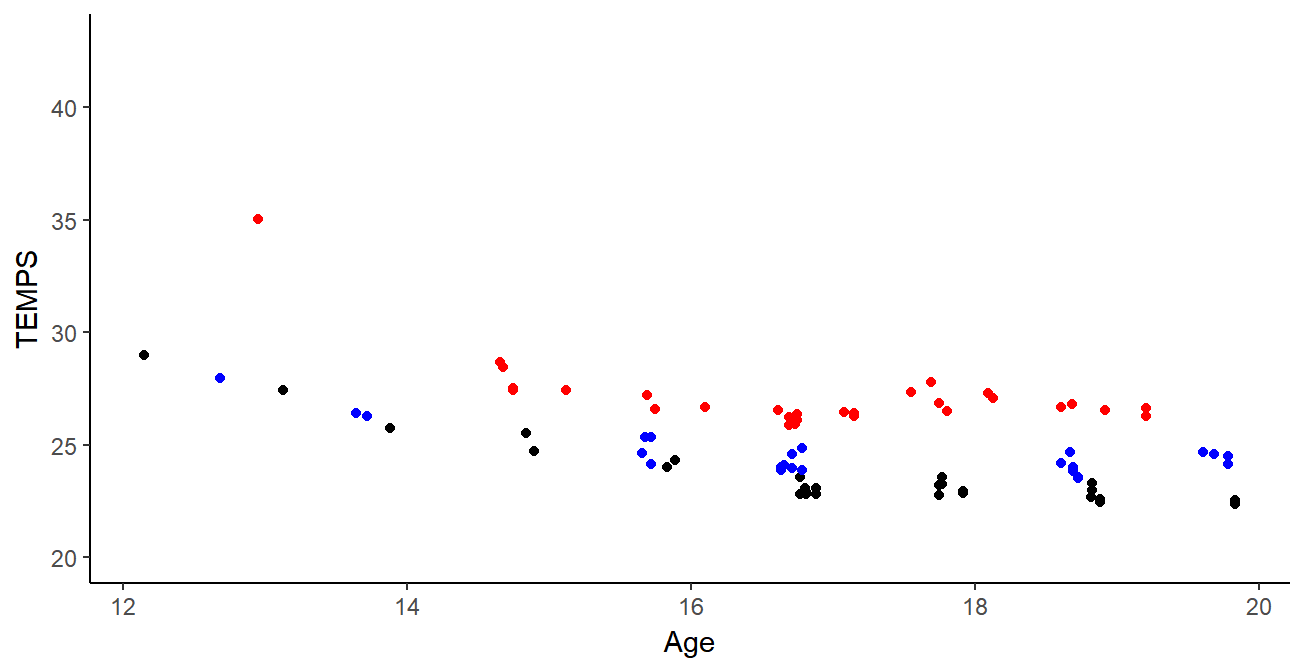
Curves clustering

Functional data \(\simeq\) coefficients \(\alpha_k\) of B-splines functions:

\[y_i(t) = \sum\limits_{k=1}^{K}{\alpha_k B_k(t)}\]

Clustering: Algo FunHDDC (gaussian mixture + EM)
Bouveyron & Jacques - 2011

Using the multidimensional version : curve + derivative
\(\rightarrow\) Information about performance level and trend of improvement

Curve clustering

Leroy et al. - 2018

• Different patterns of progression
• Consistent groups for sport experts

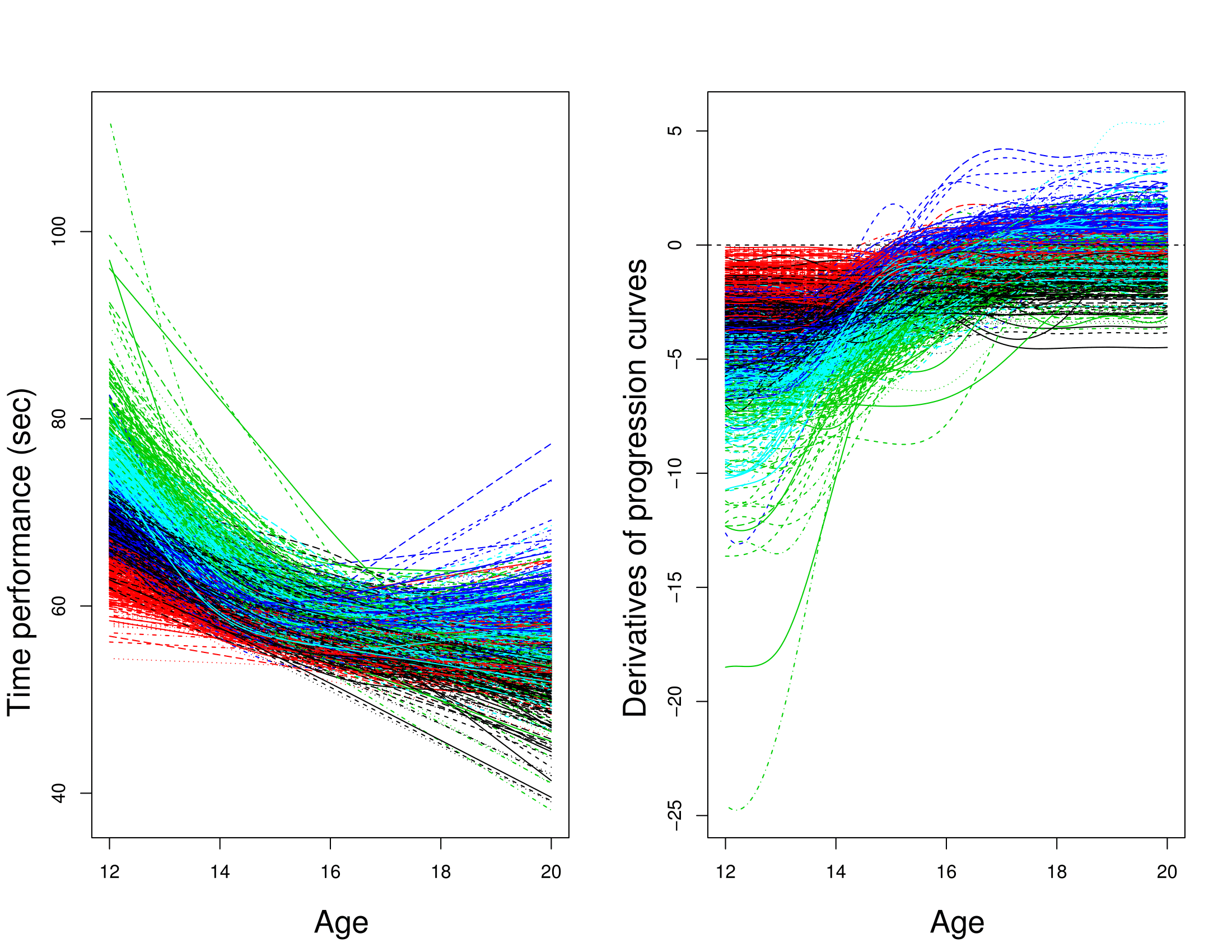
Curve clustering

Leroy et al. - 2018

• Different patterns of progression
• Consistent groups for sport experts

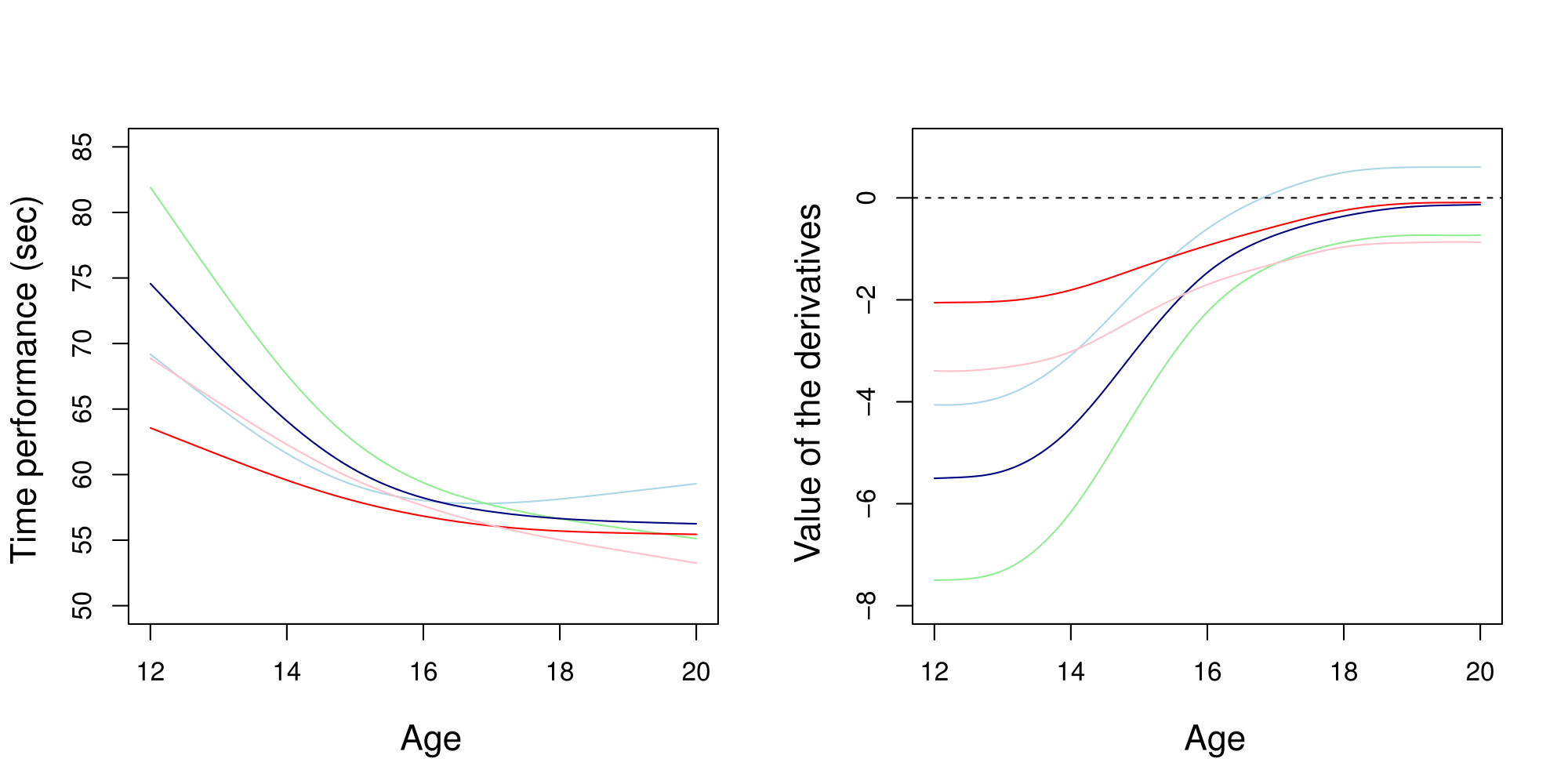
New objectives

• Prediction of the future values of the progression curve
  \(\rightarrow\) Functional regression
• Quantification of prediction uncertainty
  \(\rightarrow\) Probabilistic framework

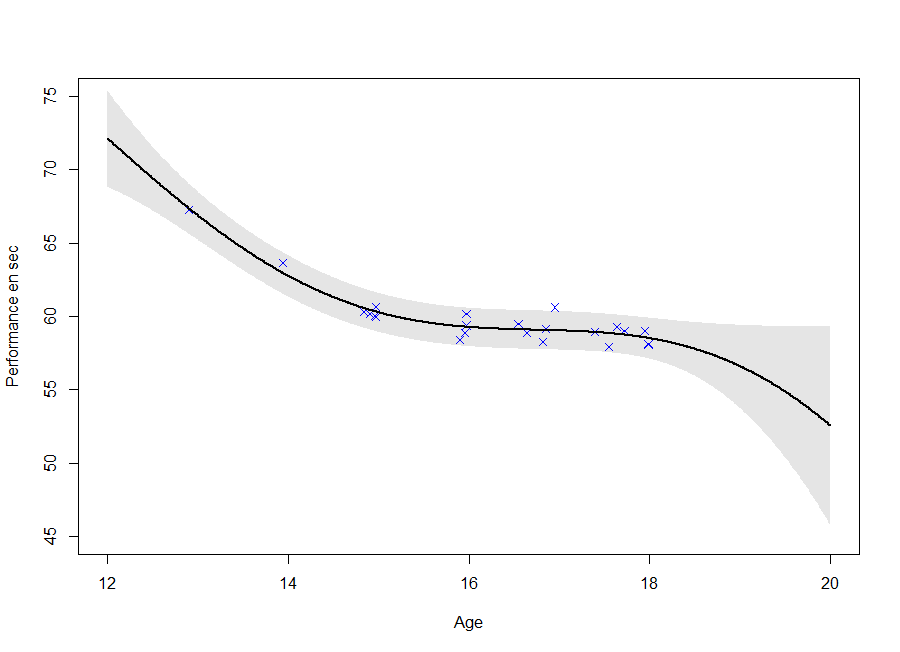
Gaussian process regression

Bishop - 2006 | Rasmussen & Williams - 2006

GPR : a kernel method to estimate \(f\) when:

\[y = f(x) +\epsilon\]

\(\rightarrow\) No restrictions on \(f\) but a prior probability:

\[f \sim \mathcal{GP}(0,C(\cdot,\cdot))\]

An example of exponential kernel for the covariance function: \[cov(f(x),f(x'))= C(x,x') = \alpha exp(- \dfrac{1}{2\theta^2} |x - x'|^2)\] Kernel definition \(\Rightarrow\) prefered properties on \(f\)

Prediction

\(\textbf{y}_{N+1} = (y_1,...,y_{N+1})\) has the following prior density: \[\textbf{y}_{N+1} \sim \mathcal{N}(0, C_{N+1}), \ C_{N+1} = \begin{pmatrix} C_N & k_{N+1} \\ k_{N+1}^T & c_{N+1} \end{pmatrix}\]

When the joint density is gaussian, so does the conditionnal dentisty:

\[y_{N+1}|\textbf{y}_{N}, \textbf{x}_{N+1} \sim \mathcal{N}(k^T \color{red}{C_N^{-1}}\textbf{y}_{N}, c_{N+1}- k_{N+1}^T \color{red}{C_N^{-1}} k_{N+1})\]

• Prediction: \(\hat{y}_{N+1} = \mathbb{E}[y_{N+1}|\textbf{y}_{N}, \textbf{x}_{N+1}]\)
• Uncertainty: CI with \(\mathbb{V}[y_{N+1}|\textbf{y}_{N}, \textbf{x}_{N+1}]\)

Visualization of GPR

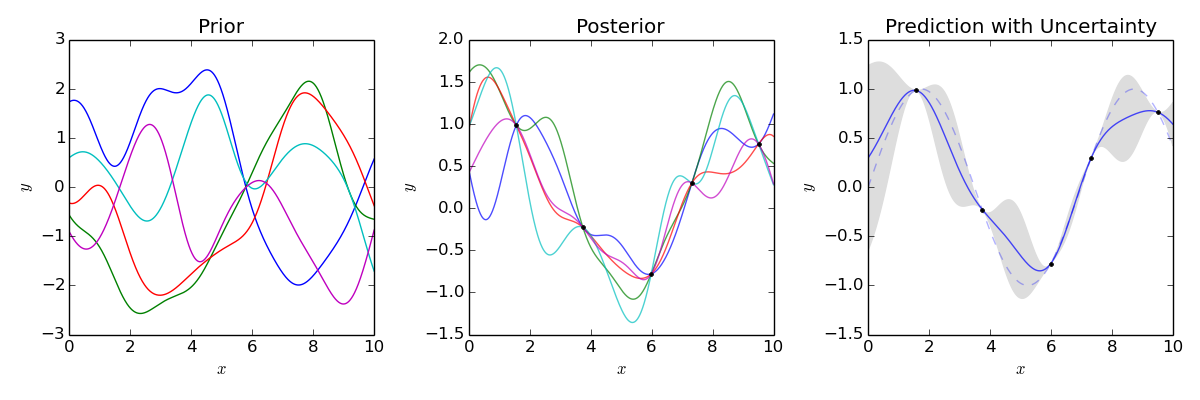
Key points:

• Define a covariance function with desirable properties
• Complexity \(O(\color{red}{N^3})\) (inversion of a \(\color{red}{N} \times \color{red}{N}\) matrix)

GP estimation from data

Estimating a GP on each individuals (\(O(\color{green}{N_i^3})\)):

• Uncertainty: Ok

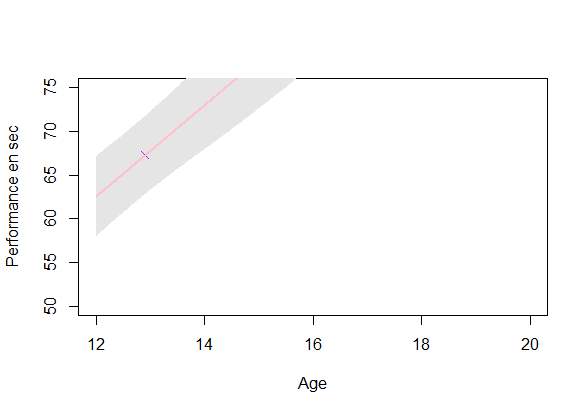
GP estimation from data

Estimating a GP on each individuals (\(O(\color{green}{N_i^3})\)):

• Uncertainty: Ok

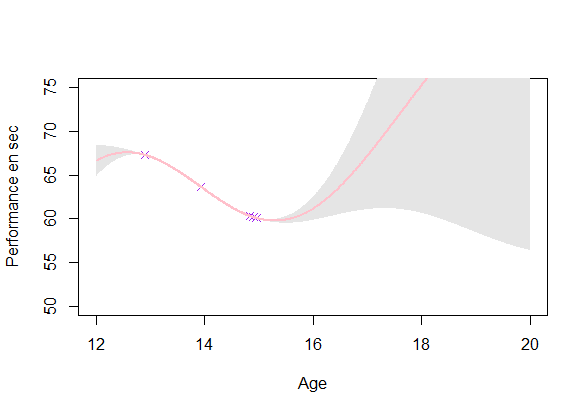
GP estimation from data

Estimating a GP on each individuals (\(O(\color{green}{N_i^3})\)):

• Uncertainty: Ok

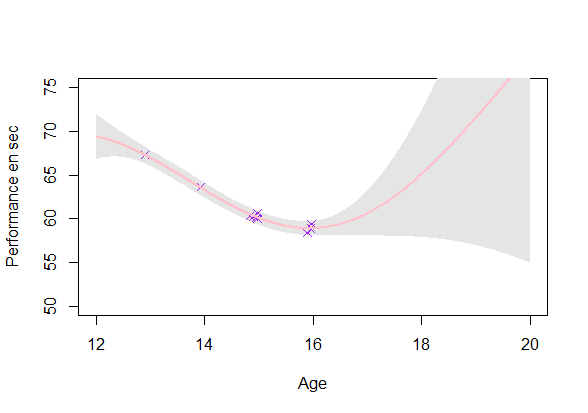
GP estimation from data

Estimating a GP on each individuals (\(O(\color{green}{N_i^3})\)):

• Uncertainty: Ok

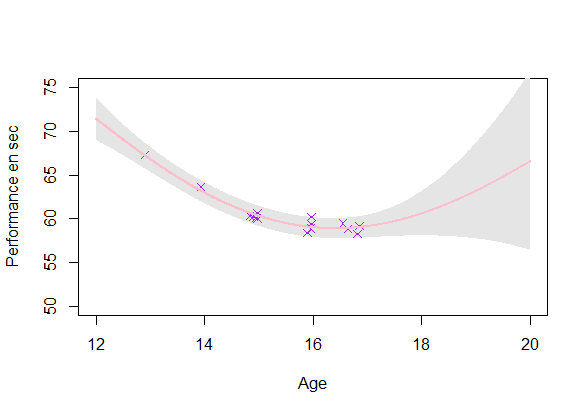
GP estimation from data

Estimating a GP on each individuals (\(O(\color{green}{N_i^3})\)):

• Uncertainty: Ok

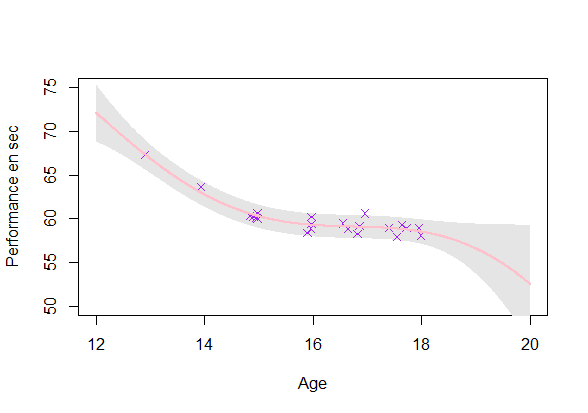
Reaching a coherent modeling

Estimating a GP on each individuals (\(O(\color{green}{N_i^3})\)):

• Uncertainty: Ok
• Coherence: Improvement required

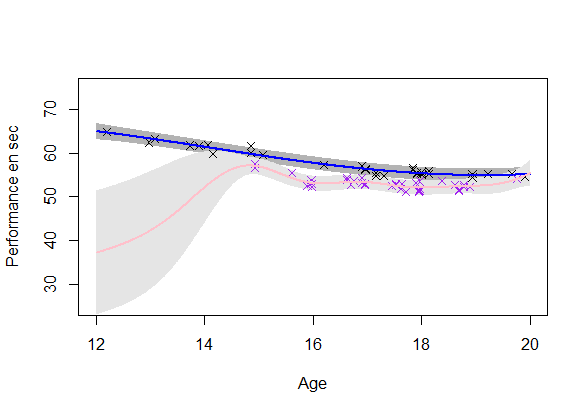
\(\rightarrow\) Using the shared information between individuals (GPR-ME)

The GPFR model

Shi & Wang - 2008 | Shi & Choi - 2011

\[Y_i(t) = \mu_0(t) + f_i(t) + \epsilon_i\] avec:

• \(f_i(\cdot) \sim \mathcal{GP}(0, \Sigma_{\theta_i}(\cdot,\cdot)), \ f_i \perp \!\!\! \perp\)
• \(\epsilon_i \sim \mathcal{N}(0, \sigma^2), \ \epsilon_i \perp \!\!\! \perp\)

GPFDA R package

Limits:

• No uncertainty about \(\mu_0\)
• Does not allow irregular time series

An extension to GPFR

\[Y_i(t) = \mu_0(t) + f_i(t) + \epsilon_i\] with:

• \(\mu_0(\cdot) \sim \mathcal{GP}(0, K_{\theta_0}(\cdot,\cdot))\)
• \(f_i(\cdot) \sim \mathcal{GP}(0, \Sigma_{\theta_i}(\cdot,\cdot)), \ f_i \perp \!\!\! \perp\)
• \(\epsilon_i \sim \mathcal{N}(0, \sigma^2), \ \epsilon_i \perp \!\!\! \perp\)

It follows that:

\[Y_i(\cdot) \vert \mu_0 \sim \mathcal{GP}(\mu_0(\cdot), \Sigma_{\theta_i}(\cdot,\cdot) + \sigma^2), \ Y_i \vert \mu_0 \perp \!\!\! \perp\]

\(\rightarrow\) Shared information through \(\mu_0\) and its uncertainty
\(\rightarrow\) Unified non parametric probabilistic framework

Notations

\(\textbf{y} = (y_1^1,\dots,y_i^k,\dots,y_M^{N_M})^T\)
\(\textbf{t} = (t_1^1,\dots,t_i^k,\dots,t_M^{N_M})^T\)
\(\Theta = \{ \theta_0, (\theta_i)_i, \sigma^2 \}\)

\(\Sigma\): covariance matrix from the process \(f_i\) evaluated on \(\textbf{t}\)

\(\Sigma = \left[ \Sigma_{\theta_i}(t_i^k, t_j^l)_{(i,j), (j,l)} \right]\)

\(\Psi = \Sigma + \sigma^2 Id_N\)

Structure of covariance matrices

Since \((Y_i)_i\vert \mu_0 \perp \!\!\! \perp\), then:

\[\Psi = \left.\left( \vphantom{\begin{array}{c}1\\1\\1\\1\\1\\1\end{array}} \smash{ \begin{array}{cccccc} \Psi_1&0&\cdots &\cdots&0\\ \vdots&\ddots&&\ddots&\vdots\\ 0&&\Psi_i &&0\\ \vdots&\ddots&&\ddots&\\ 0&\cdots&\cdots&0 &\Psi_M \end{array} } \right)\right\} \,\color{red}{N} \times \color{red}{N} \]

\[\Psi_i = \left.\left( \vphantom{\begin{array}{c}1\\1\end{array}} \smash{ cov(y(t_i^l),y(t_i^k))_{l,k} } \right)\right\} \,\color{green}{N_i}\times\color{green}{N_i}\]

Learning HP and \(\mu_0\)

Step E: Computing the posterior

\[p(\mu_0(\textbf{t}) \vert \textbf{t}, \textbf{y}, \Theta) = \mathcal{N}( \hat{\mu}_0(\textbf{t}), \hat{K})\]

Efficiently computable if \(K_{\theta_0}\) is block diagonal

Step M: Estimating \(\Theta\)

\[\hat{\Theta} = \underset{\Theta}{\arg\max} \ \mathbb{E}_{\mu_0} [ \log \ p(\textbf{y}, \mu_0(\textbf{t}) \vert \textbf{t}, \Theta ) \ \vert \Theta]\]

    Initialize hyperparameters
    while(sufficient condition of convergence){
    Iterate alternatively steps E and M}

Conclusion

• For a new time \(t^*\), we have a posterior density for \(Y_i(t^*)\)

• Prediction + uncertainty for future performances

• Split a \(O(\color{red}{N^3})\) problem into \(M \ O(\color{green}{N_i^3})\) problems

• Remains computationaly extensive but tractable

• Code available soon on https://github.com/ArthurLeroy

Perspectives

• Mixture of GP to perform cluster-specific predictions

• Study and design of different covariance functions

• Using several other variables, multivariate functional regression

• Application to other sports (track and field, rowing, …)

References