Multi-Mean Gaussian Processes: A novel probabilistic framework for multi-correlated longitudinal data

Arthur Leroy - Department of Computer Science, The University of Manchester

joint work with

- Mauricio Alvarez - Department of Computer Science, The University of Manchester

- Dennis Wang - Department of Computer Science, The University of Sheffield

- Ai Ling Teh - Singapore Institute for Clinical Sciences

NeurIPS Workshop on Gaussian Processes, Spatiotemporal Modeling, and Decision-making Systems - 02/12/2022

Longitudinal data observed from multiple irregular sources

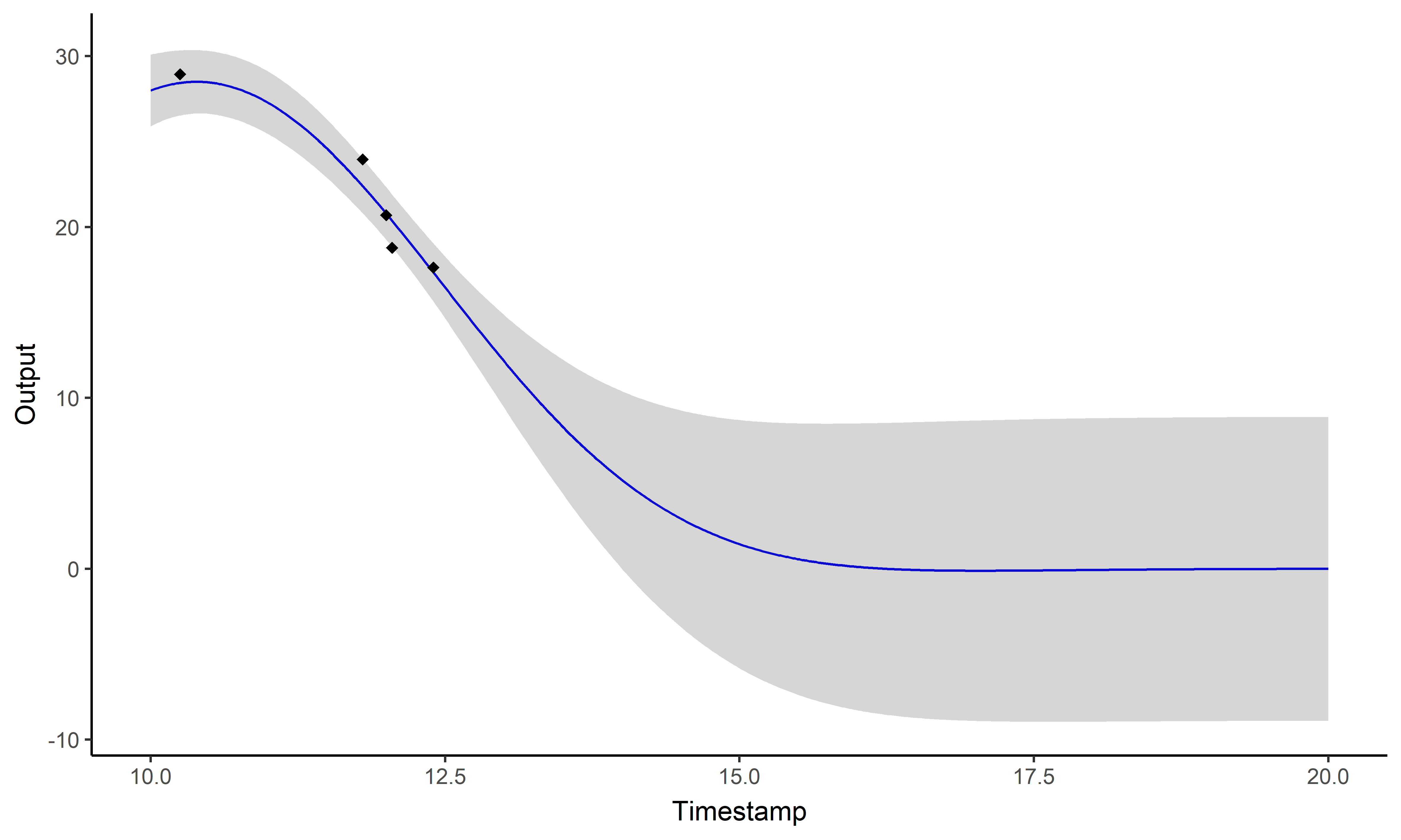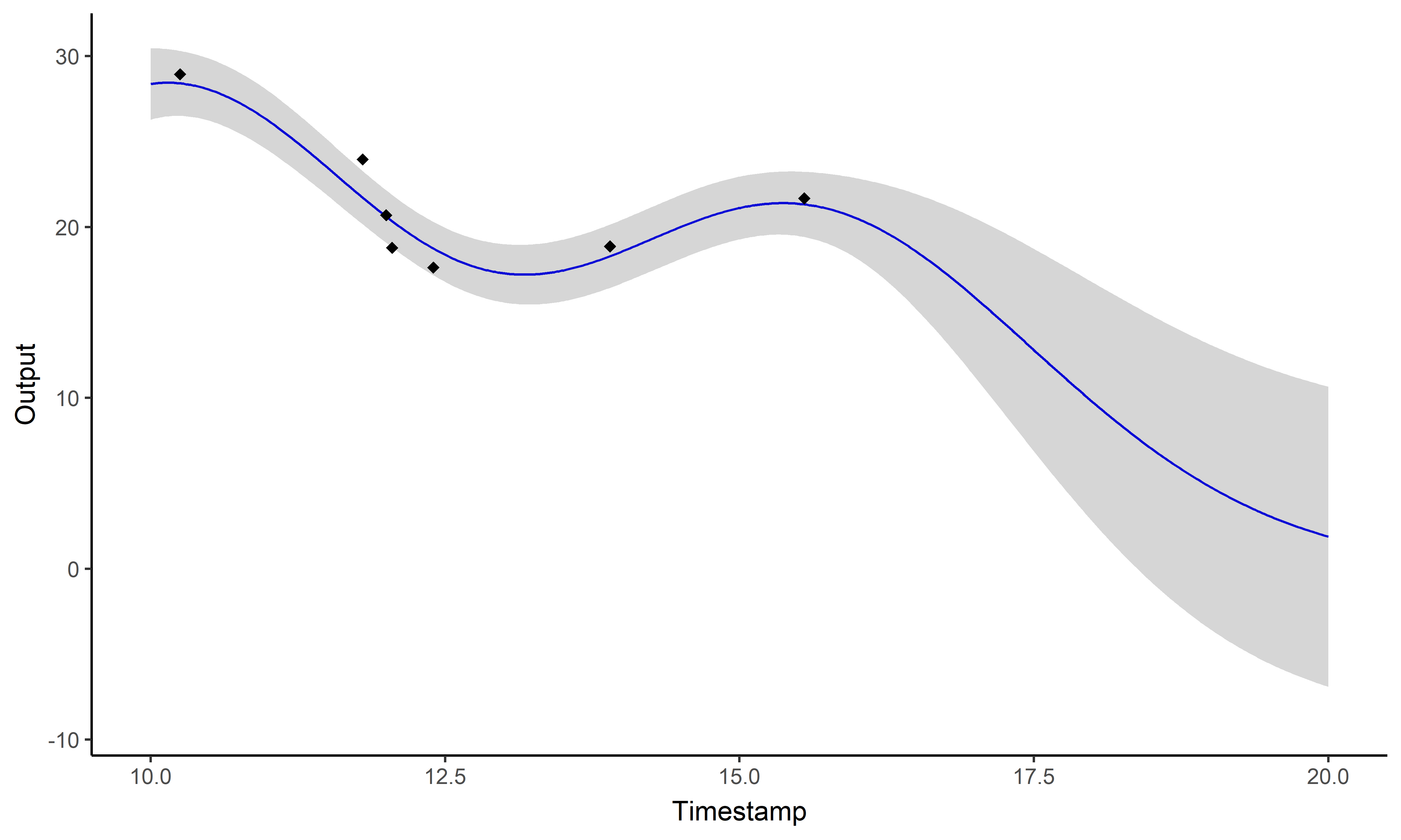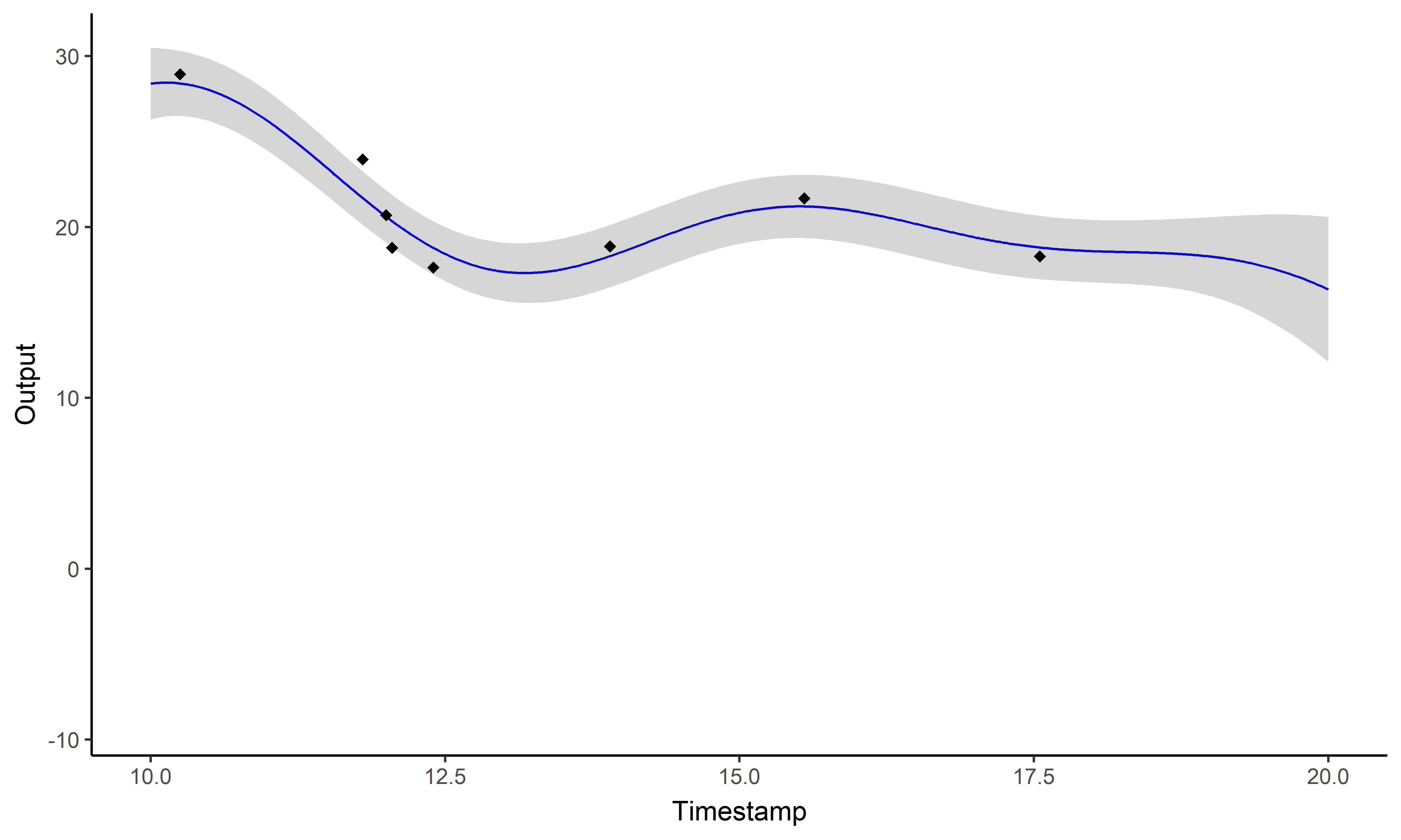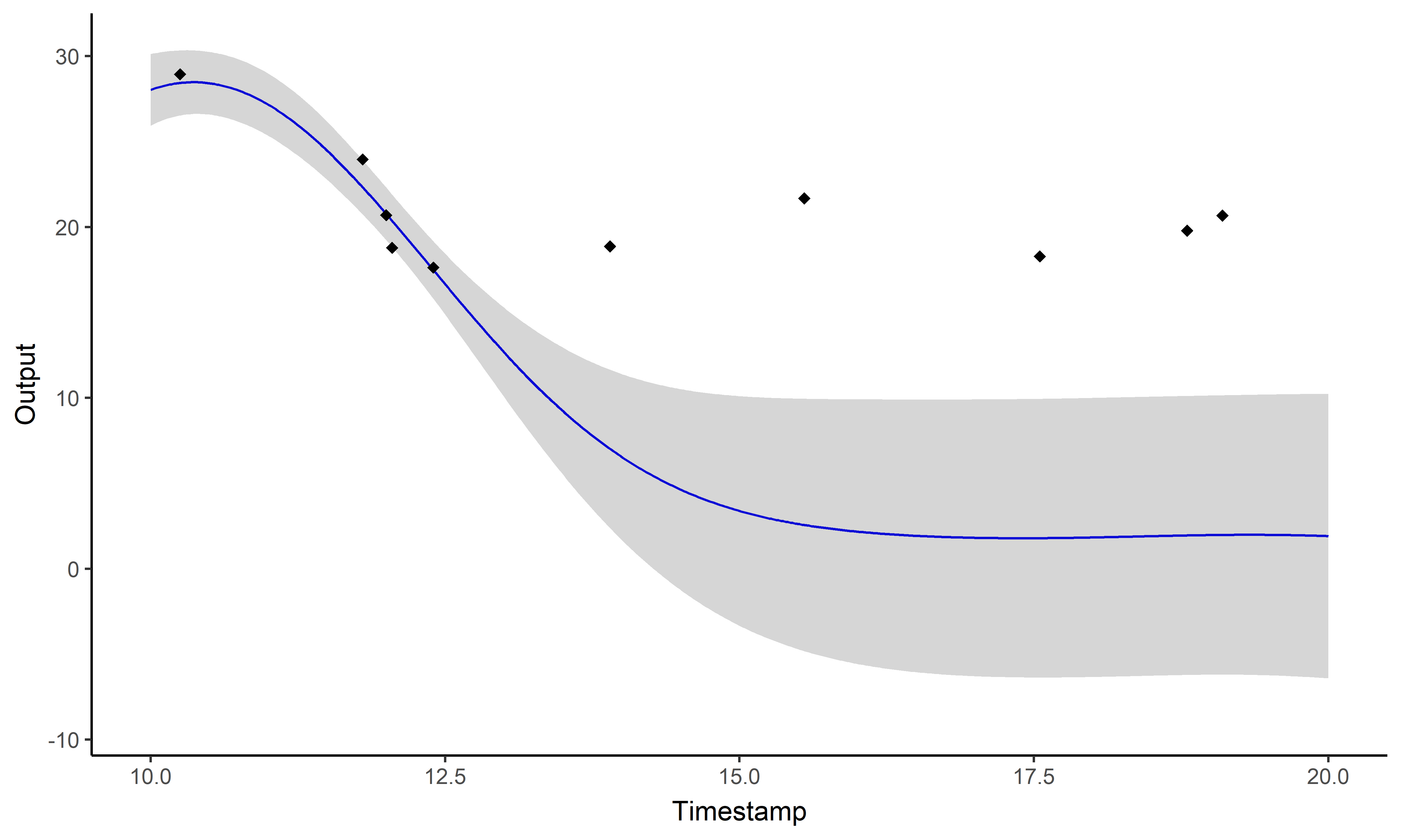
Gaussian processes offers an elegant and well-suited framework for modelling longitudinal data.

Until then, most multi-task approaches focus on the covariance structure. Let us present a novel multi-task GP paradigm sharing information through a common mean process.

Leroy et al. - Magma: Inference and Prediction using Multi-Task Gaussian Processes with Common Mean - Machine Learning - 2022

\[y_i = \mu_0 + f_i + \epsilon_i\]

with: \(\ \ \ \mu_0 \sim \mathcal{GP}(m_0, K_{\theta_0}), \ \ \ f_i \sim \mathcal{GP}(0, \Sigma_{\theta_i}), \ \ \ \epsilon_i \sim \mathcal{GP}(0, \sigma_i^2)\)

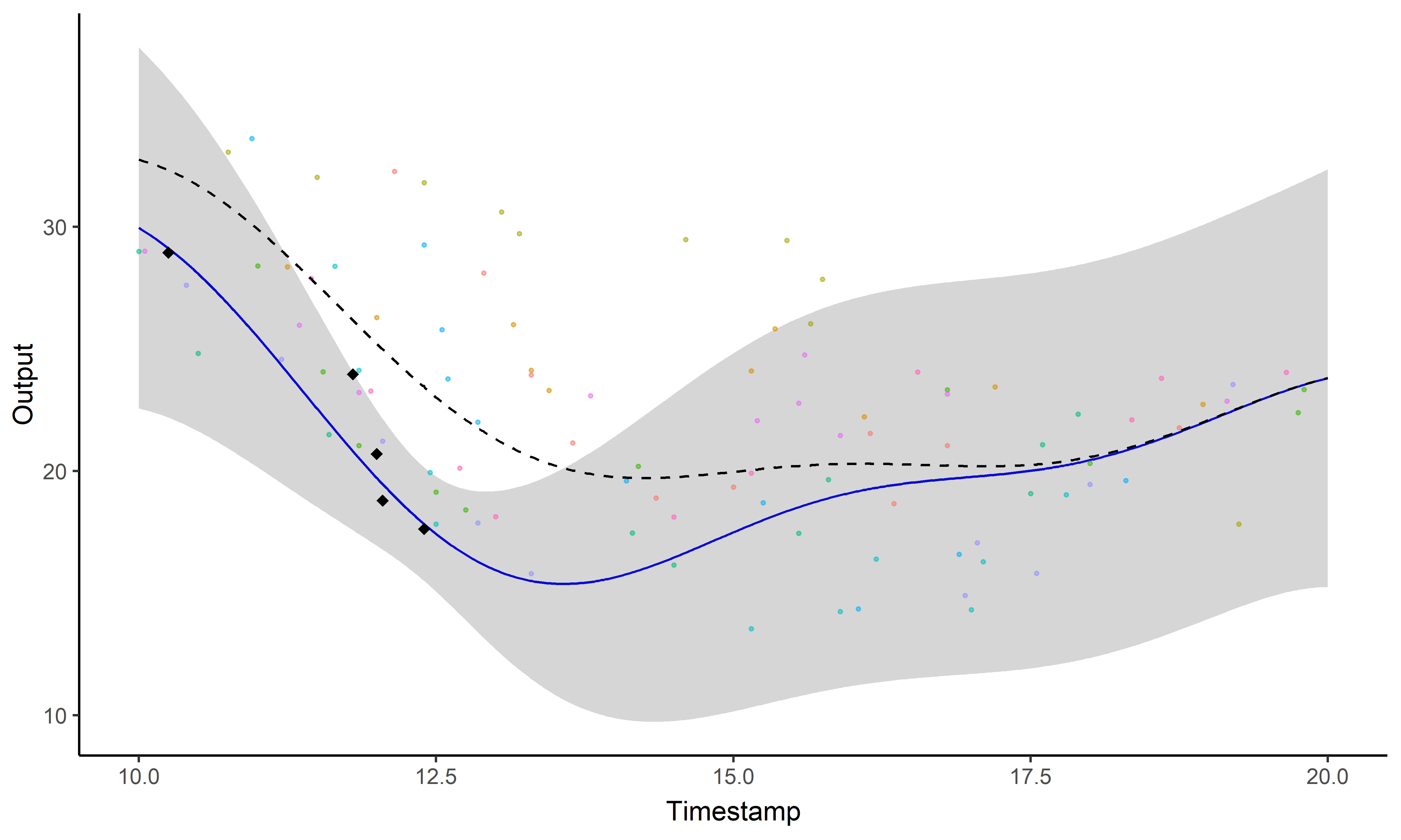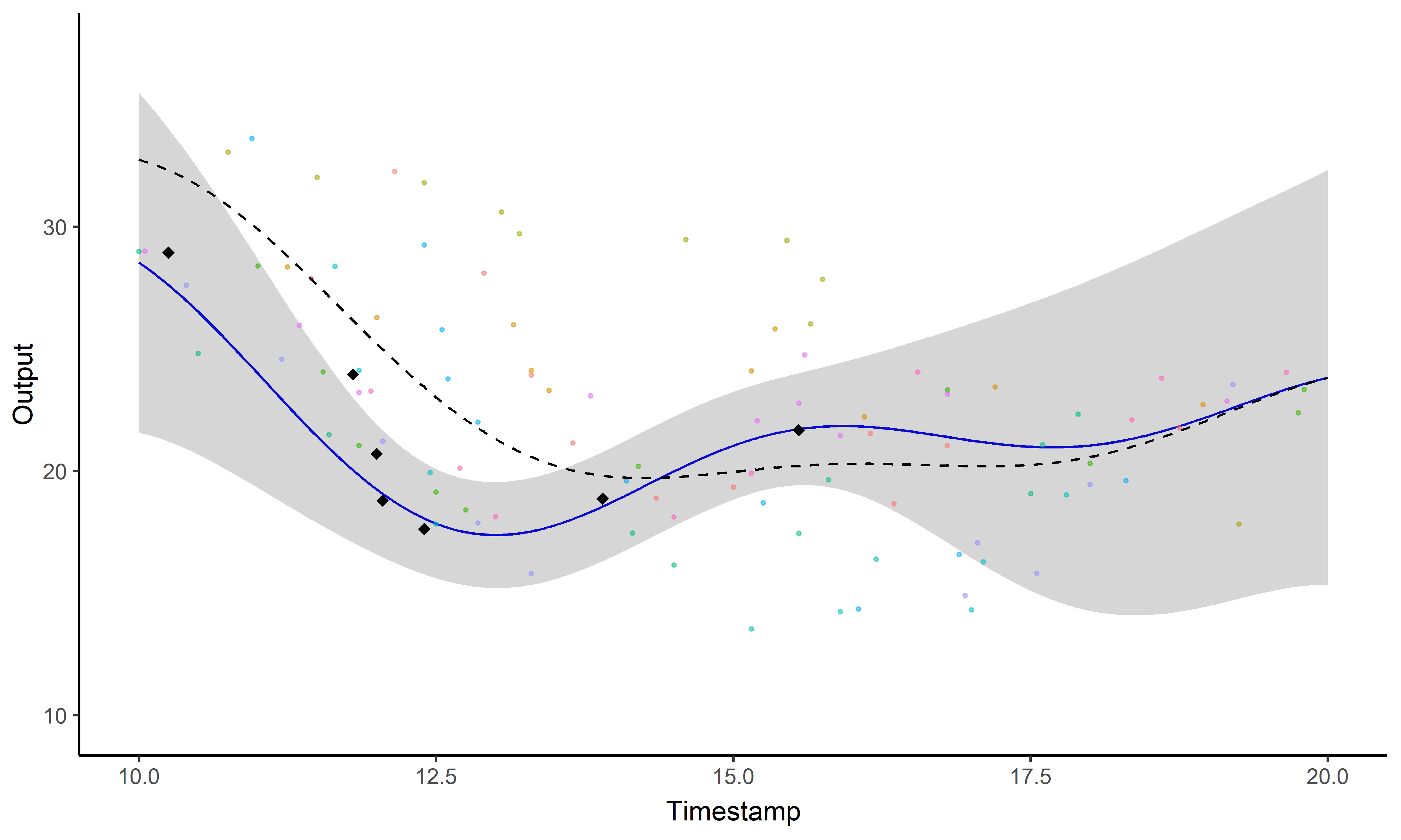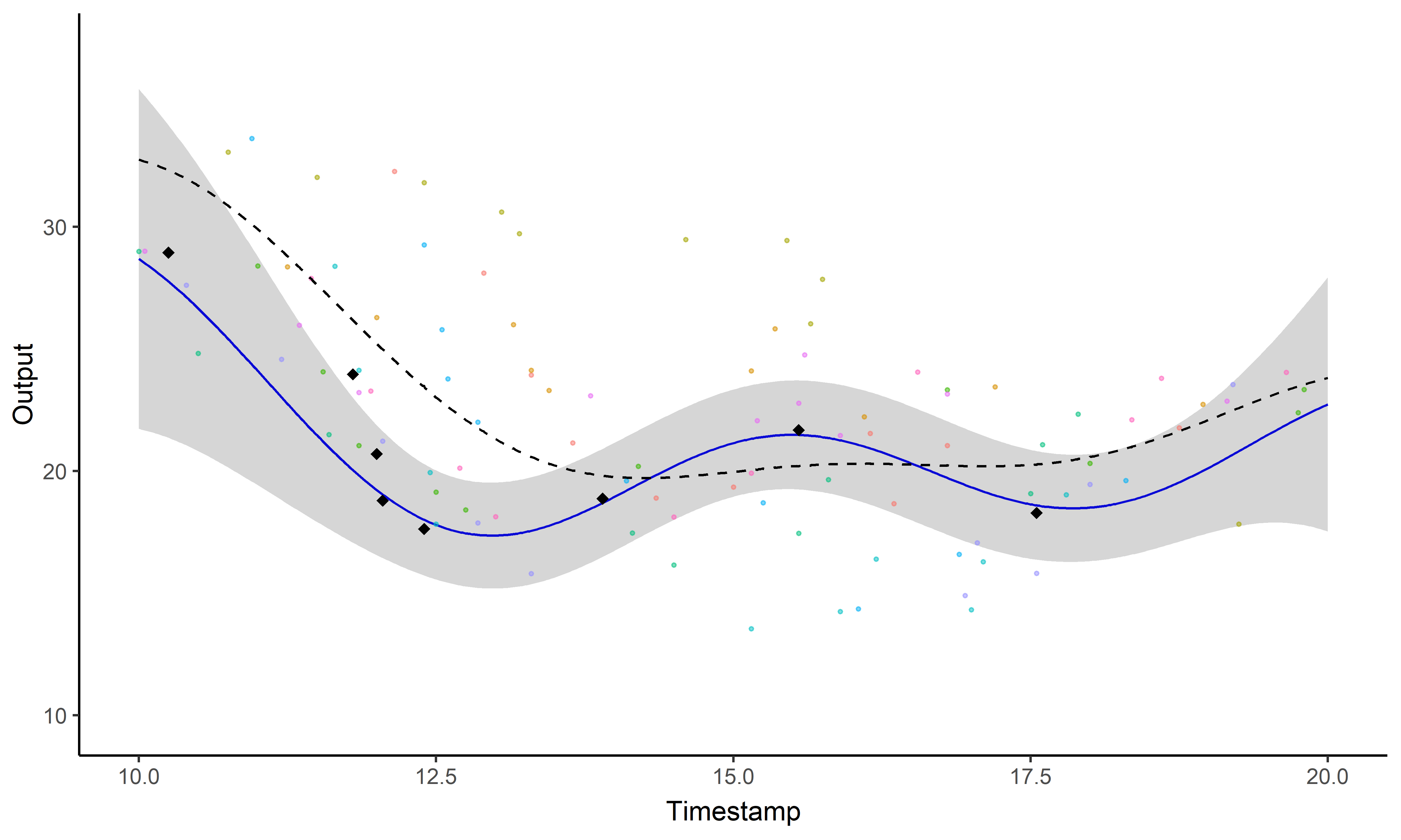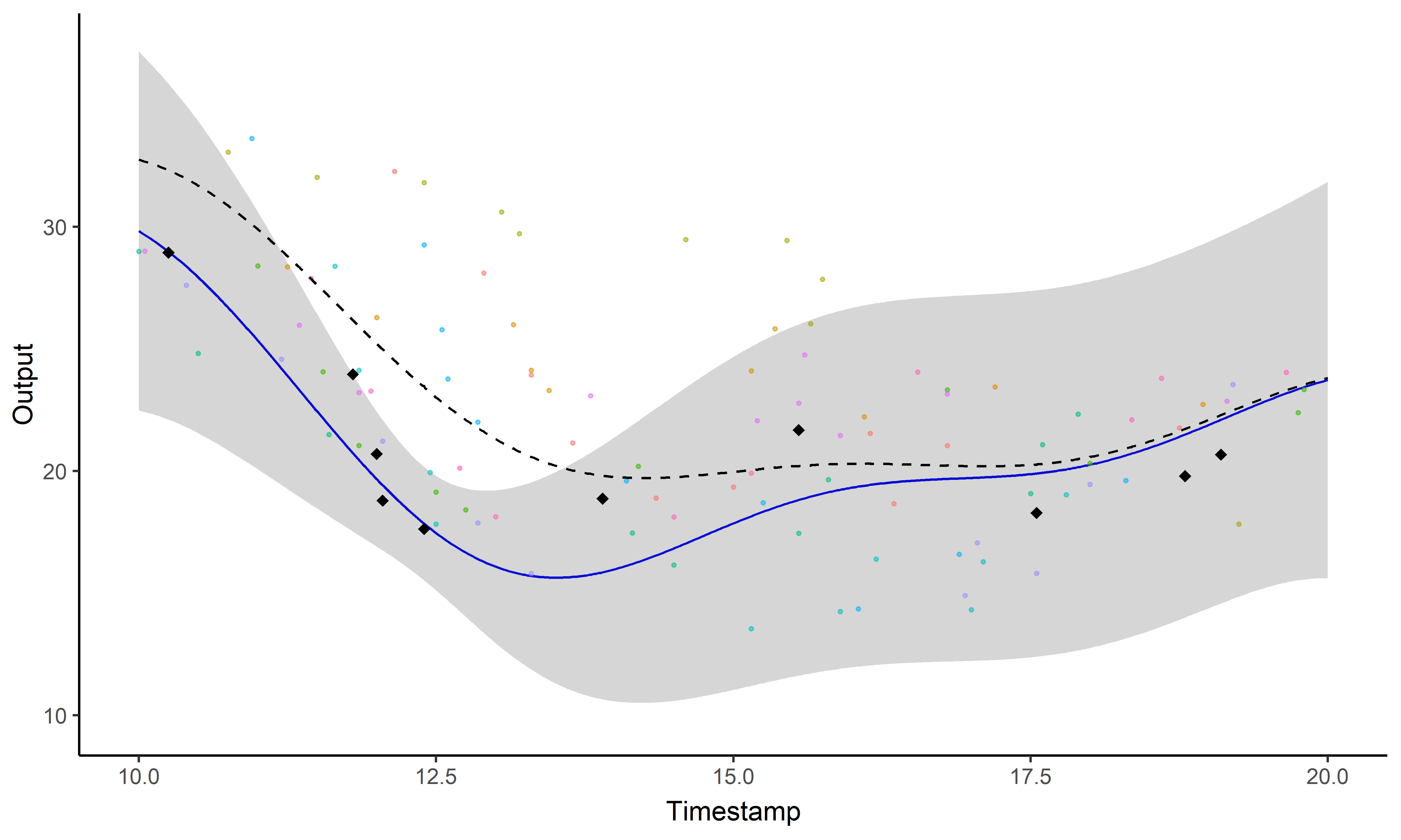
Leroy et al. - Cluster-Specific Predictions with Multi-Task Gaussian Processes - Accepted in JMLR - 2022

\[y_i \mid \{\color{orange}{Z_{ik}} = 1 \} = \mu_{\color{orange}{k}} + f_i + \epsilon_i\]

with: \(\ \ \ \color{orange}{Z_{i}} \sim \mathcal{M}(1,\color{orange}{\boldsymbol{\pi}}), \ \ \ \mu_{\color{orange}{k}} \sim \mathcal{GP}(m_{\color{orange}{k}}, \color{orange}{C_{\gamma_{k}}}), \ \ \ f_i \sim \mathcal{GP}(0, \Sigma_{\theta_i}), \ \ \ \epsilon_i \sim \mathcal{GP}(0, \sigma_i^2).\)

Implemented as an R package MagmaClustR: https://github.com/ArthurLeroy/MagmaClustR

Multi-Mean Gaussian processes framework

\[y_{\color{blue}{i}\color{red}{j}} = \mu_{0} + f_\color{blue}{i} + g_\color{red}{j} + \epsilon_{\color{blue}{i}\color{red}{j}}\]

Key idea: compute multiple dedicated posterior mean processes

\[p(\mu_0 \mid \{y_{\color{blue}{i}\color{red}{j}} \}_{\color{blue}{i} = 1,\dots, \color{blue}{M}}) = \mathcal{N}\Big(\mu_{0}; \ \hat{m}_{\color{red}{j}}, \hat{K}_\color{red}{j} \Big), \ \forall \color{red}{j} \in 1, \dots, \color{red}{P}\] \[p(\mu_0 \mid \{y_{\color{blue}{i}\color{red}{j}} \}_{\color{red}{j} = 1,\dots, \color{red}{P}}) = \mathcal{N}\Big(\mu_{0}; \ \hat{m}_{\color{blue}{i}}, \hat{K}_\color{blue}{i} \Big), \forall \color{blue}{i} \in 1, \dots, \color{blue}{M} \]