Apprentissage et données fonctionnelles:
Application au problème de la détection dans le sport de haut niveau

Contexte

La détection aujourd’hui :
\(\rightarrow\) Meilleurs jeunes + intuition entraineurs

G. Boccia et al. (2017) :

\(\simeq\) 60% des top jeunes à 16 ans ne maintiennent pas leur niveau étant adultes

Philip E. Kearney & Philip R. Hayes (2018) :

\(\simeq\) 10% seulement du top 20 sénior était
top 20 en - 13 ans

Approche data-driven

Objectifs: Clustering et prédiction de séries temporelles. Problèmes classiques mais données très irrégulières:

• Nombre d’observations différents entre individus
• Instants d’observation différents entre individus
• Peu d’observations par individu

\(\rightarrow\) Analyse de données fonctionnelles

Les données

Base de données de la Fédération Française de Natation sur l’exhausitivité des performances des licenciés depuis 2002 :

• 10 000 000 performances
• \(\simeq\) X0 000 observations et \(\simeq\) 1 000 individus par épreuves

Les données

Base de données de la Fédération Française de Natation sur l’exhausitivité des performances des licenciés depuis 2002 :

• 10 000 000 performances
• \(\simeq\) X0 000 observations et \(\simeq\) 1 000 individus par épreuves

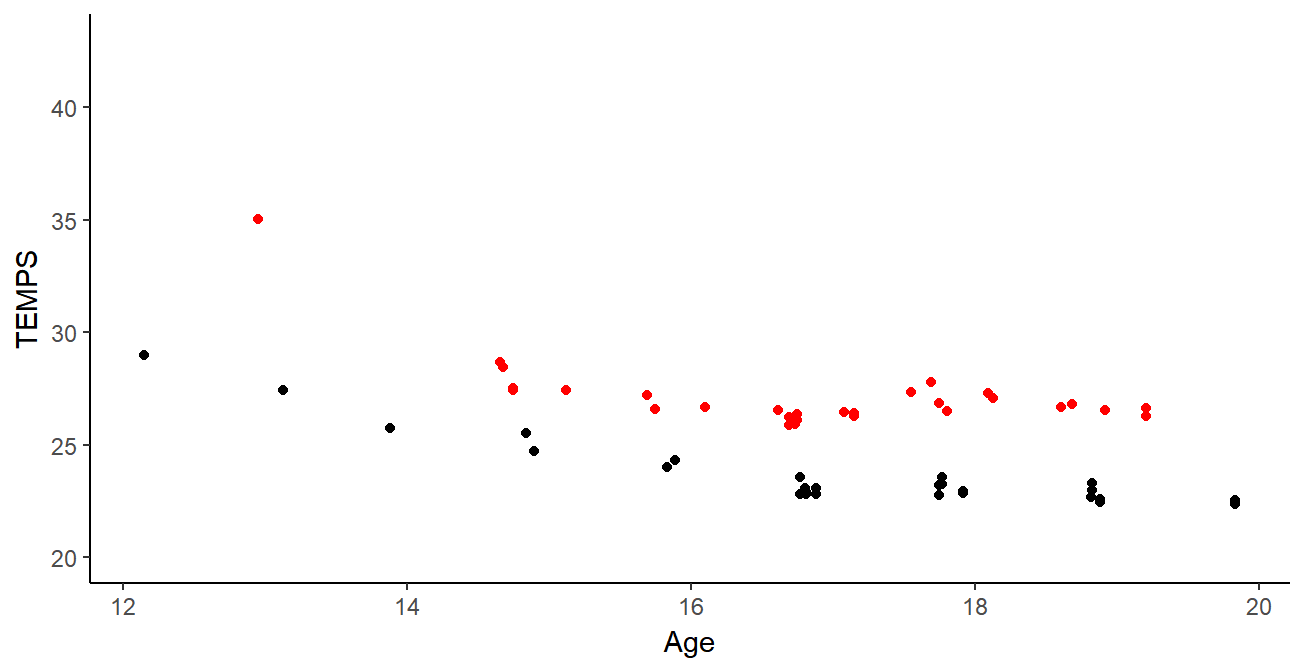
Les données

Base de données de la Fédération Française de Natation sur l’exhausitivité des performances des licenciés depuis 2002 :

• 10 000 000 performances
• \(\simeq\) X0 000 observations et \(\simeq\) 1 000 individus par épreuves

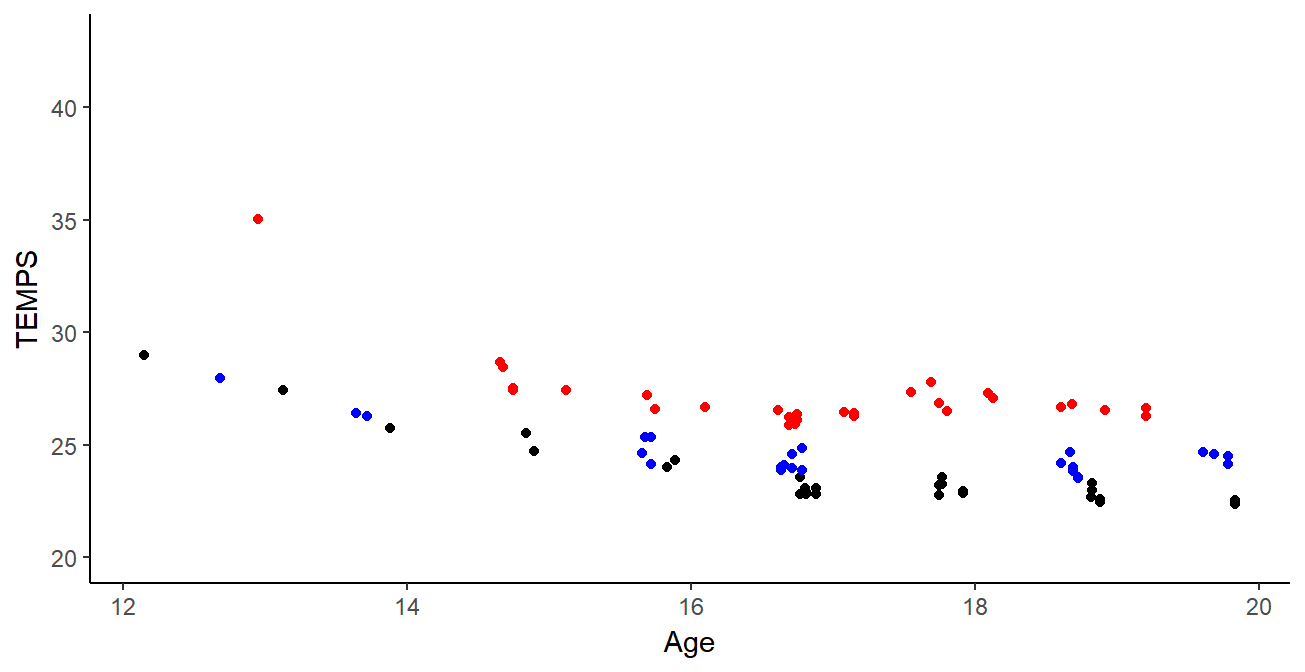
Les données

Base de données de la Fédération Française de Natation sur l’exhausitivité des performances des licenciés depuis 2002 :

• 10 000 000 performances
• \(\simeq\) X0 000 observations et \(\simeq\) 1 000 individus par épreuves
• Lissage par fonctions de bases B-splines

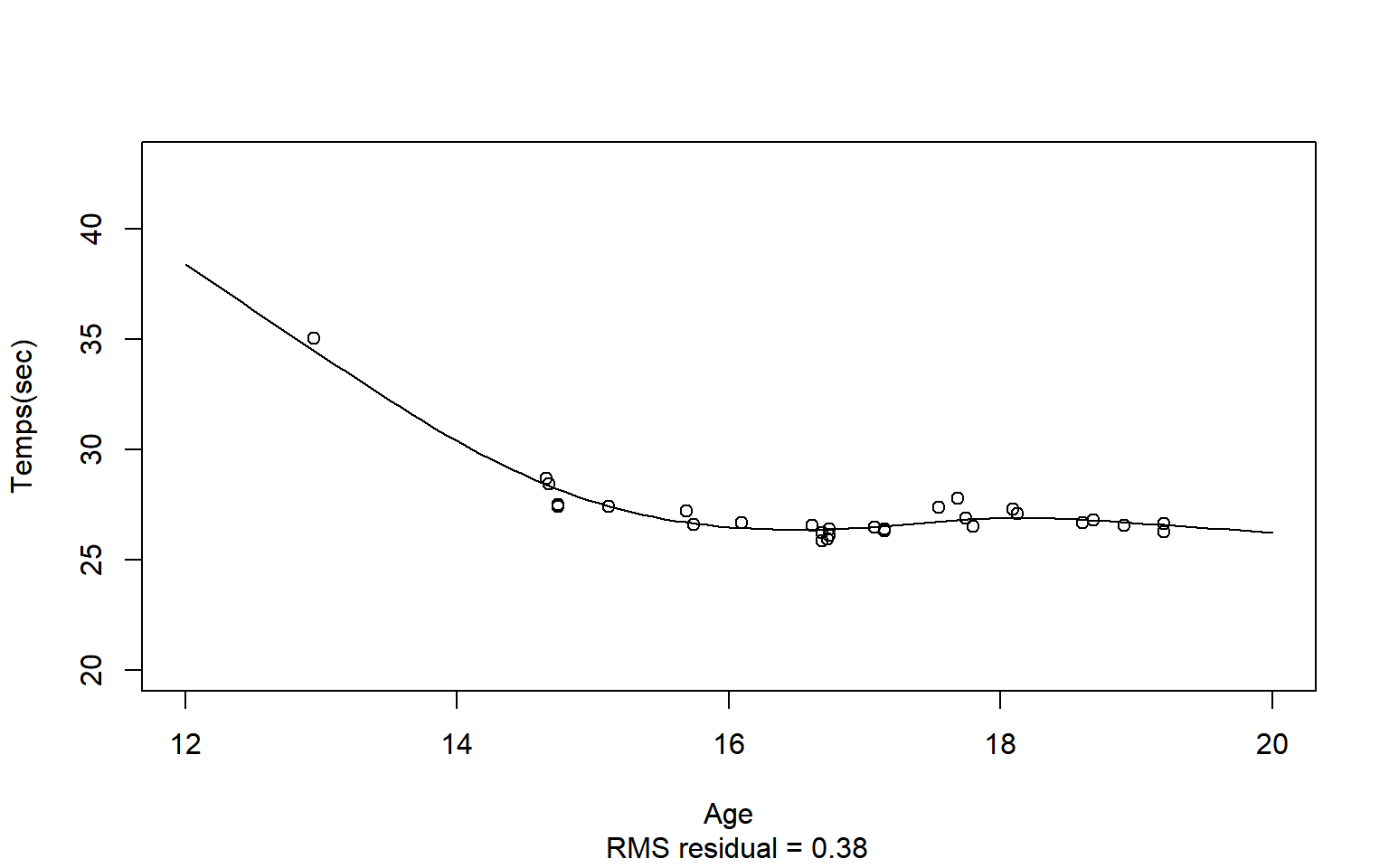
Approche paramétrique

Donnée fonctionnelle \(\simeq\) coefficients \(\alpha_k\) des B-splines :

\[y_i(t) = \sum\limits_{k=1}^{K}{\alpha_k B_k(t)}\]

Clustering: Algo FunHDDC (mélange Gaussienne + EM)
Bouveyron & Jacques - 2011

Utilisation version multidimensionnelle : courbe + dérivée \(\rightarrow\) information de niveau et de dynamique de progression

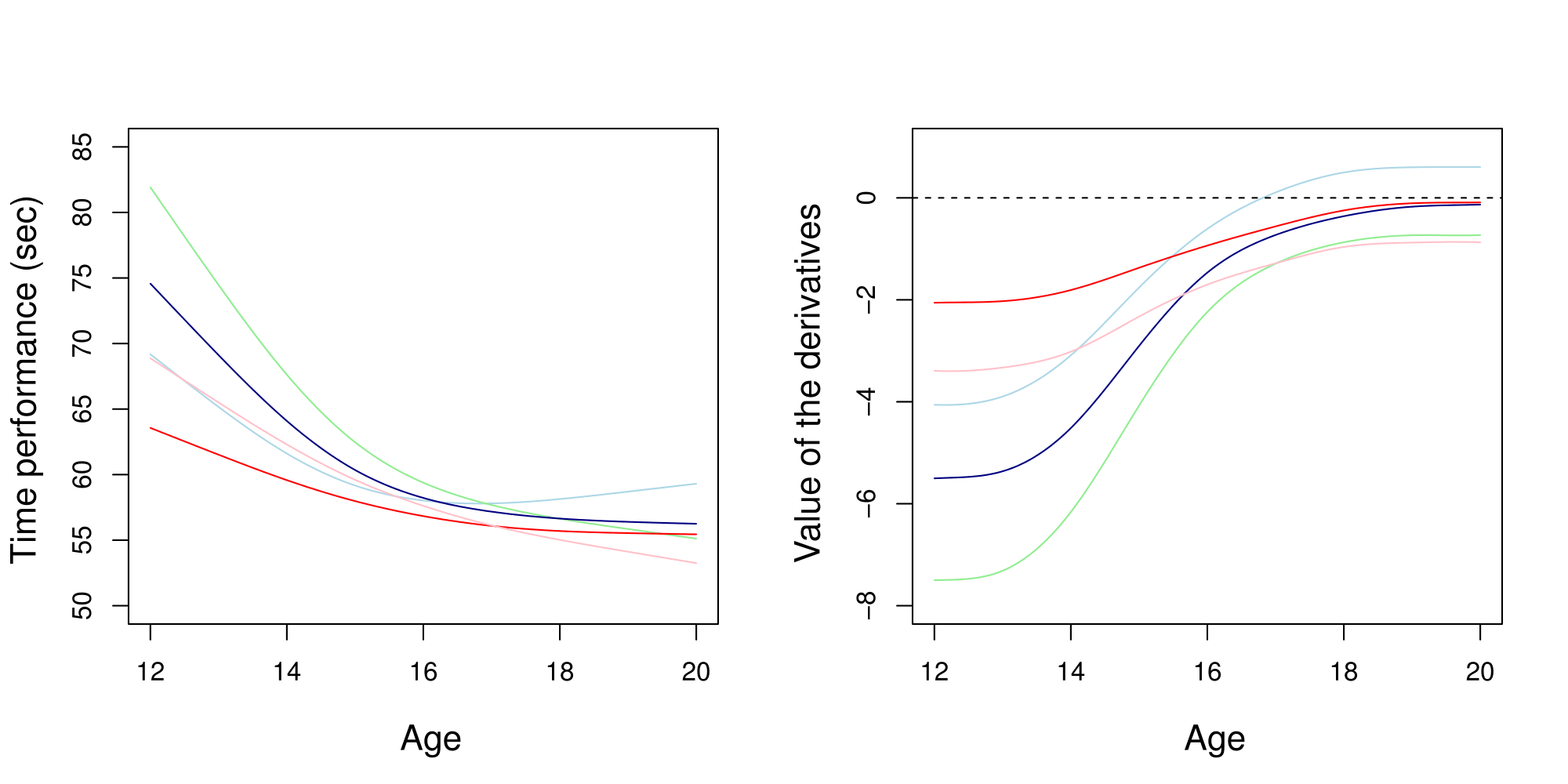
Clustering de courbes

Résultats:

• Plus d’informations en ajoutant courbes + dérivées
• Groupes cohérents pour les experts sportifs

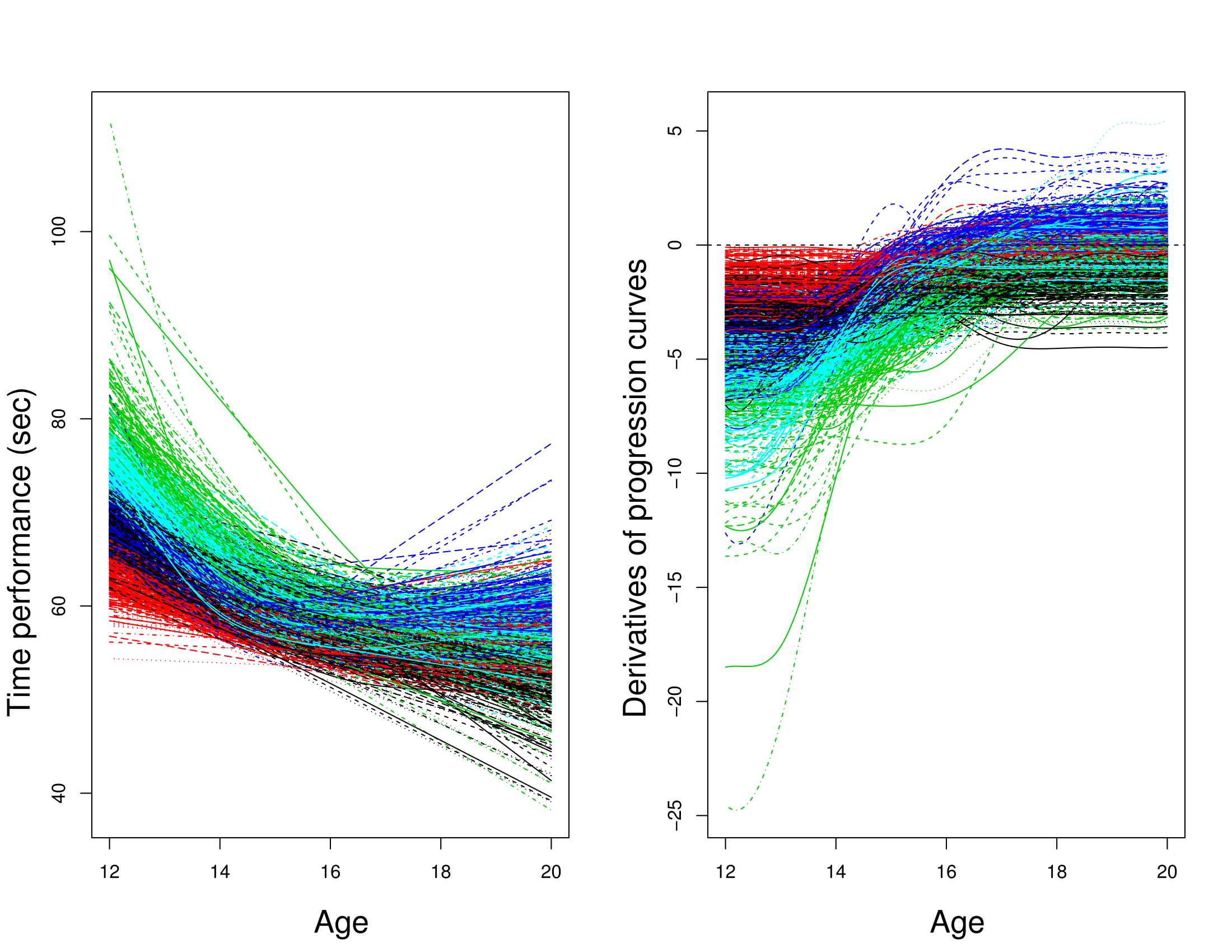
Clustering de courbes

Résultats:

• Plus d’informations en ajoutant courbes + dérivées
• Groupes cohérents pour les experts sportifs

Les limites

• Quelques modélisations individuelles insatisfaisantes
• Pas d’information sur l’incertitude de modélisation
• Limites de l’approche paramétrique pour la prédiction

En résumé: cadre paramétrique + fréquentiste valide pour étudier des moyennes de groupes mais insuffisant pour des prédictions individuelles fiables.

\(\rightarrow\) Cadre probabiliste non paramétrique des processus Gaussiens

Régression par Processus Gaussiens

Bishop - 2006 | Rasmussen & Williams - 2006

GPR : méthode à noyau pour estimer \(f\) lorsque:

\[y = f(x) +\epsilon\]

\(\rightarrow\) Pas de restrictions sur \(f\) mais une probabilité a priori

\[f \sim \mathcal{GP}(0,C(\cdot,\cdot))\]

Exemple de noyau exponentiel pour fonction de covariance: \[cov(f(x),f(x'))= C(x,x') = \alpha exp(- \dfrac{1}{2\theta^2} |x - x'|^2) + \delta_{ij}\sigma^2\] Forme du noyau \(\Rightarrow\) propriétés de \(f\) favorisées a priori

La prédiction

\(\textbf{y}_{N+1} = (y_1,...,y_{N+1})\) de loi jointe a priori: \[\textbf{y}_{N+1} \sim \mathcal{N}(0, C_{N+1}), \ C_{N+1} = \begin{pmatrix} C_N & k_{N+1} \\ k_{N+1}^T & c_{N+1} \end{pmatrix}\]

Or, si la loi jointe est Gaussienne, la conditionnelle aussi et:

\[y_{N+1}|\textbf{y}_{N}, \textbf{x}_{N+1} \sim \mathcal{N}(k^T C_N^{-1}\textbf{y}_{N}, c_{N+1}- k_{N+1}^T C_{N+1}k_{N+1}) \]

• Prédiction: \(\hat{y}_{N+1} = \mathbb{E}[y_{N+1}|\textbf{y}_{N}, \textbf{x}_{N+1}]\)
• Incertitude: IC avec \(\mathbb{V}[y_{N+1}|\textbf{y}_{N}, \textbf{x}_{N+1}]\)

La GPR en image

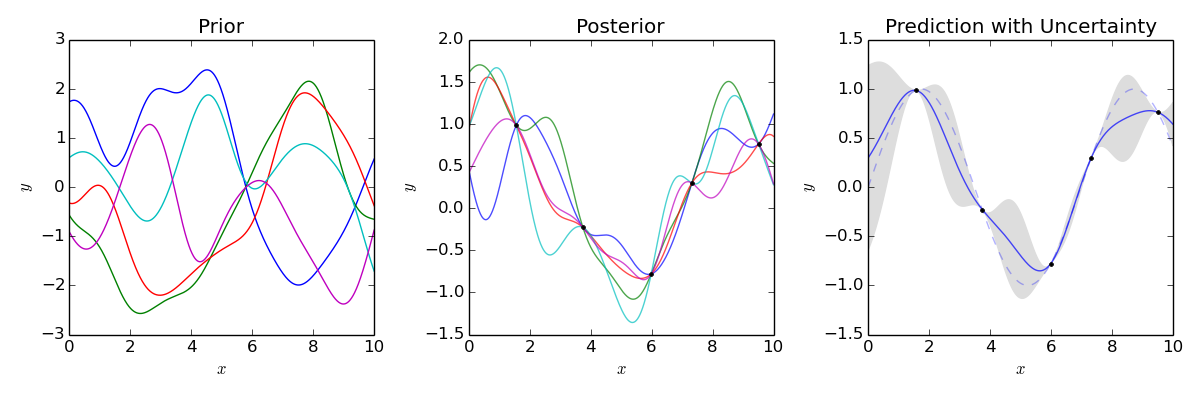
Principales difficultés:

• Définir fonction de covariance avec propriétés voulues
• Estimation en \(O(N^3)\) (inversion matrice \(N \times N\))

Une modélisation cohérente

Estimation d’un GP par individu:

• Incertitude: Ok
• Cohérence: A revoir

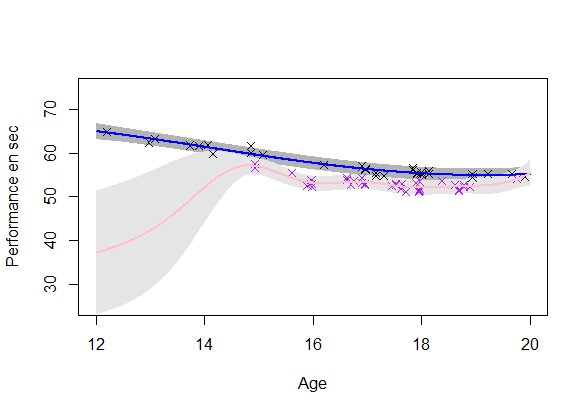
\(\rightarrow\) Utilisation d’un modèle mixte

Le modèle GPR-ME

Shi & Wang - 2008 | Wang & Khardon - 2012 | Yang & al - 2017

\[Y_i(t) = \mu_0(t) + f_i(t) + \epsilon_i\] avec:

• \(\mu_0(\cdot) \sim \mathcal{GP}(0, K_{\theta_0}(\cdot,\cdot))\)
• \(f_i(\cdot) \sim \mathcal{GP}(0, \Sigma_{\theta_i}(\cdot,\cdot)), \ f_i \perp \!\!\! \perp\)
• \(\epsilon_i \sim \mathcal{N}(0, \sigma^2), \ \epsilon_i \perp \!\!\! \perp\)

On a donc:

\[Y_i(\cdot) \vert \mu_0 \sim \mathcal{GP}(\mu_0(\cdot), \Sigma_{\theta_i}(\cdot,\cdot) + \sigma^2), \ Y_i \vert \mu_0 \perp \!\!\! \perp \]

Apprentissage des HP et \(\mu_0\)

\(\textbf{y} = (y_1^1,\dots,y_i^k,\dots,y_M^{N_M})^T\)
\(\textbf{t} = (t_1^1,\dots,t_i^k,\dots,t_M^{N_M})^T\)
\(\Theta = \{ \theta_0, (\theta_i)_i, \sigma^2 \}\)

Etape E: Calculer la loi a posteriori

\[p(\mu_0(\textbf{t}) \vert \textbf{t}, \textbf{y}, \Theta) = \mathcal{N}( \hat{\mu}_0(\textbf{t}), \hat{K})\]

Sous réserve que \(K_{\theta_0}\) soit diagonale par blocs

Etape M: Estimer \(\Theta\)

\[\hat{\Theta} = \underset{\Theta}{\arg\max} \ \mathbb{E}_{\mu_0} [ log \ p(\textbf{y}, \mu_0(\textbf{t}) \vert \textbf{t}, \Theta ) \ \vert \Theta]\]

La prédiction (travail en cours)

Pour un nouveau temps \(t_i^*\), prédire \(y_i^*\).

Problème: Que vaut \(\mu_0(t_i^*)\) ?

Une fois résolu, on aura:

\[y_i^* \vert \textbf{y}_i, \textbf{t}_i, t_i^*, \mu_0 \sim \mathcal{N}(m^*, v^*)\]
Prédiction:
\(m^* = \mu_0(t_i^*) + \Sigma_{\theta_i}(\textbf{t}_i,t^*)^T \Sigma_{\theta_i}^{-1}\textbf{y}_i\)
Incertitude: \(v^* = \Sigma_{\theta_i}(t^*,t^*) - \Sigma_{\theta_i}(\textbf{t}_i,t^*)^T \Sigma_{\theta_i}^{-1}\Sigma_{\theta_i}(\textbf{t}_i,t^*)\)

Implémentation et applications

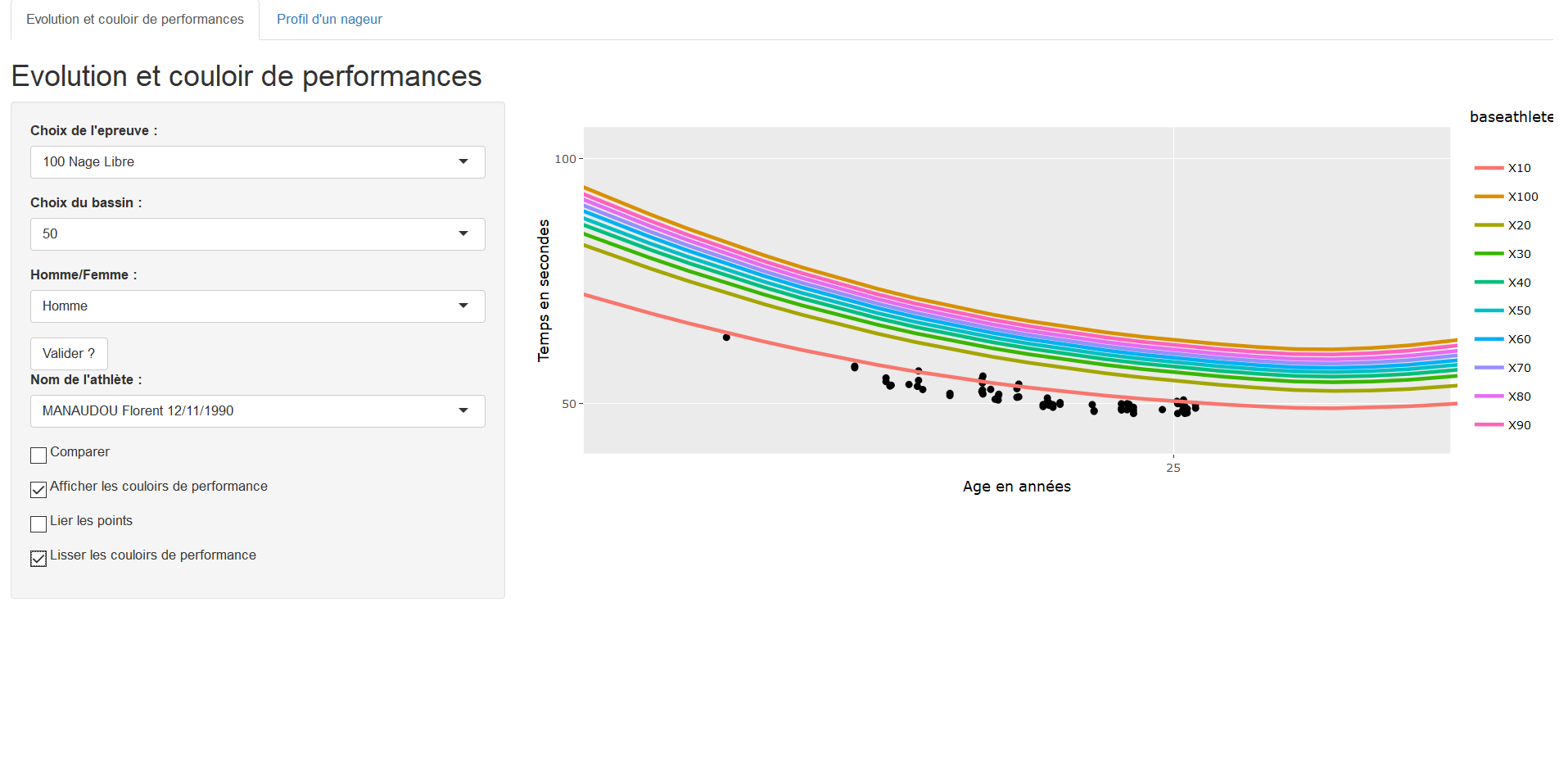
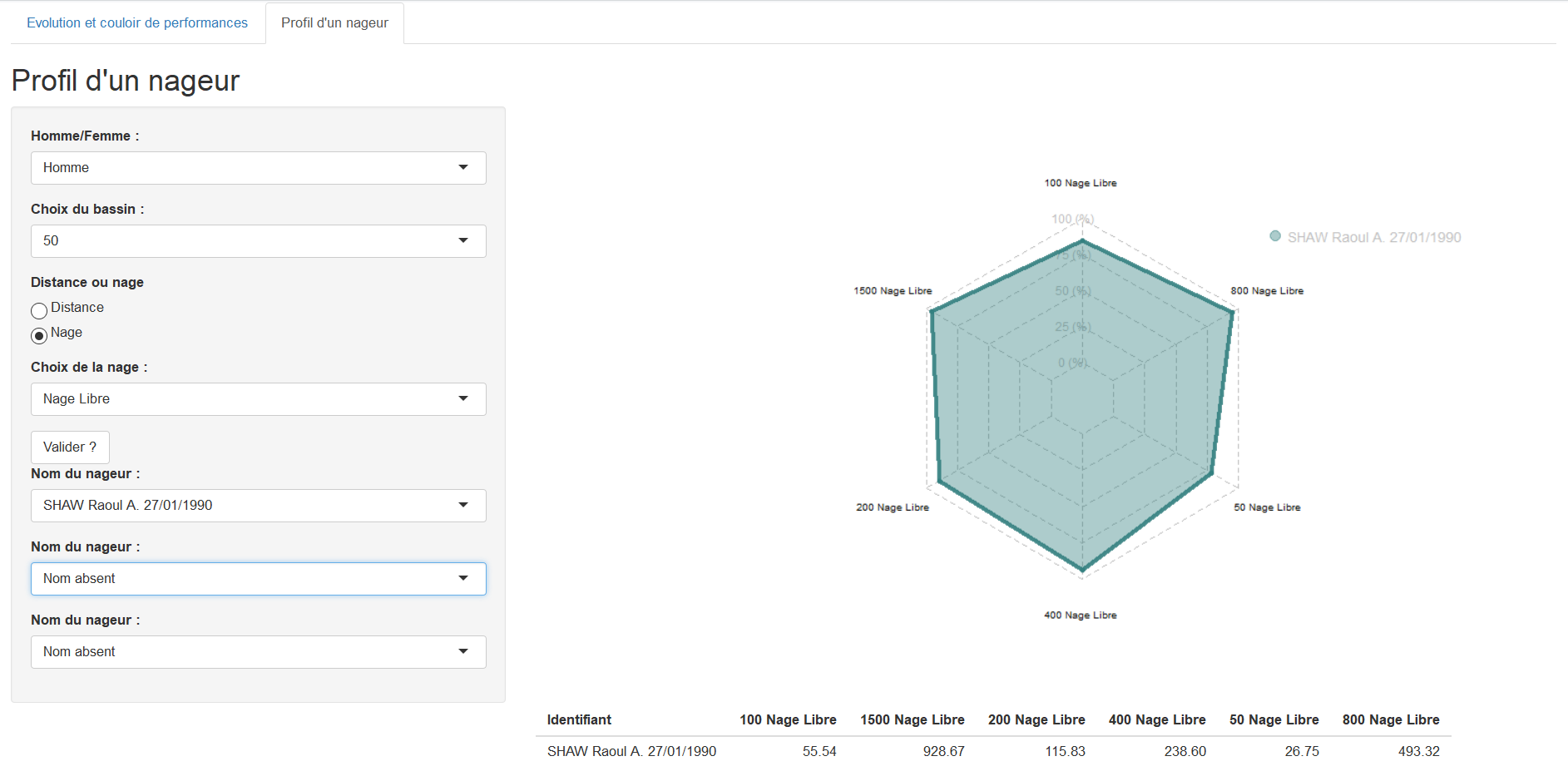
• Modification des systèmes de sélection
  
• Déploiement d’une appli web sur les serveurs FFN et formation des cadres techniques

Perspectives

• Mélange de GP pour une prédiction cluster-spécifique

• Etude et design de différentes fonctions de covariance

• Utilisation d’autres variables, régression fonctionnelle multivariée (et/ou mixte)

• Application à d’autres sports (Athlétisme, Aviron, …) et implémentation

Références