![image alt <]()
![image alt >]()
Cluster-Specific Predictions with Multi-Task Gaussian Processes
Arthur Leroy - Department of Computer Science, The University of Manchester
Pierre Latouche - Université Clermont Auvergne, CNRS, LMBP,
Benjamin Guedj - Centre for Artificial Intelligence, University College London & Inria London
Servane Gey - Université Paris Cité, CNRS, MAP5
40th International Conference on Machine
Learning

Gaussian processes offers an elegant
and well-suited framework for modelling longitudinal data.
Until then, most multi-task approaches focus on the covariance structure. Let us present a novel multi-task GP paradigm sharing information through a common mean process.
\[y_i = \mu_0 + f_i + \epsilon_i\]
with: \(\ \ \ \mu_0 \sim
\mathcal{GP}(m_0, K_{\theta_0}), \ \ \ f_i \sim \mathcal{GP}(0,
\Sigma_{\theta_i}), \ \ \ \epsilon_i \sim \mathcal{GP}(0,
\sigma_i^2)\)
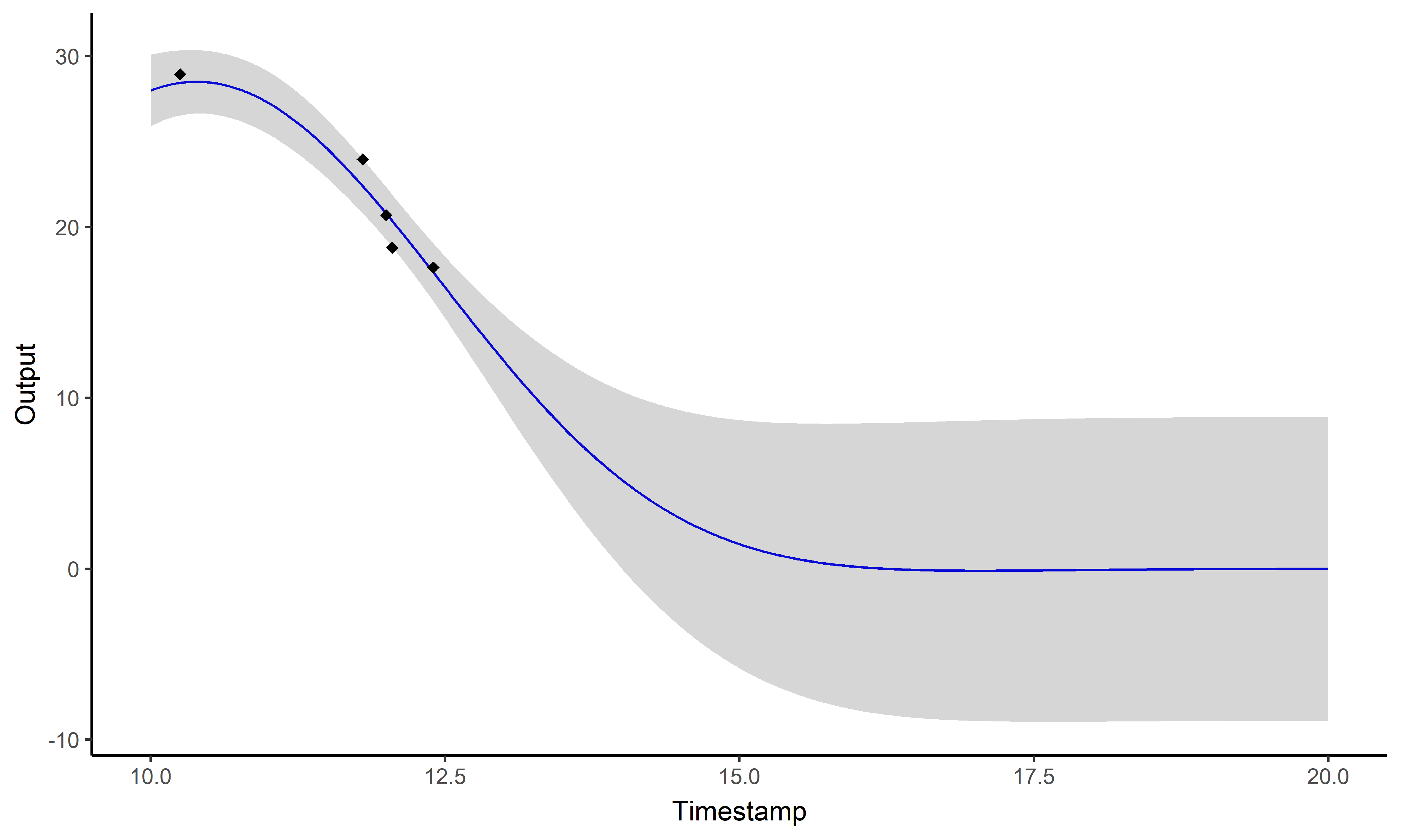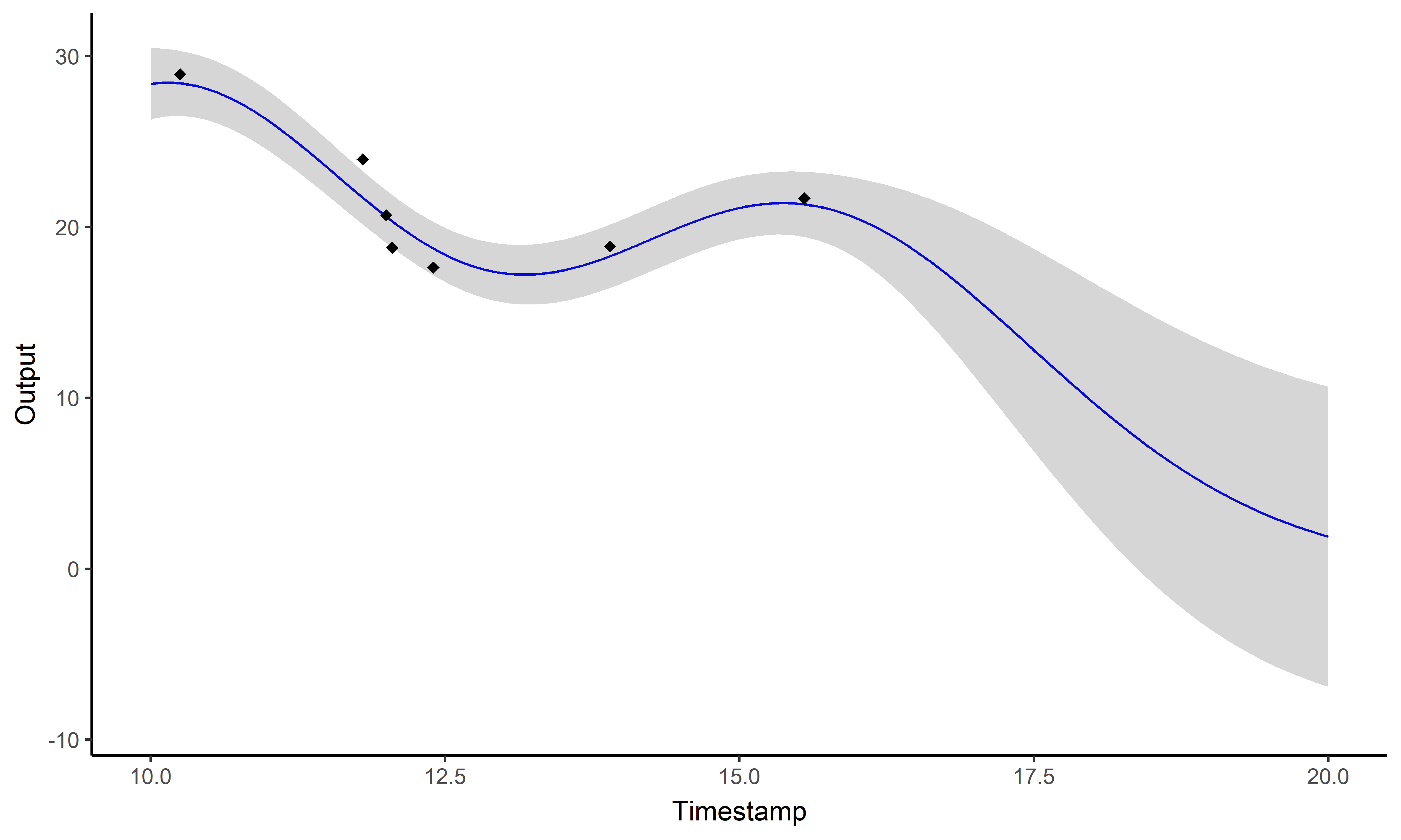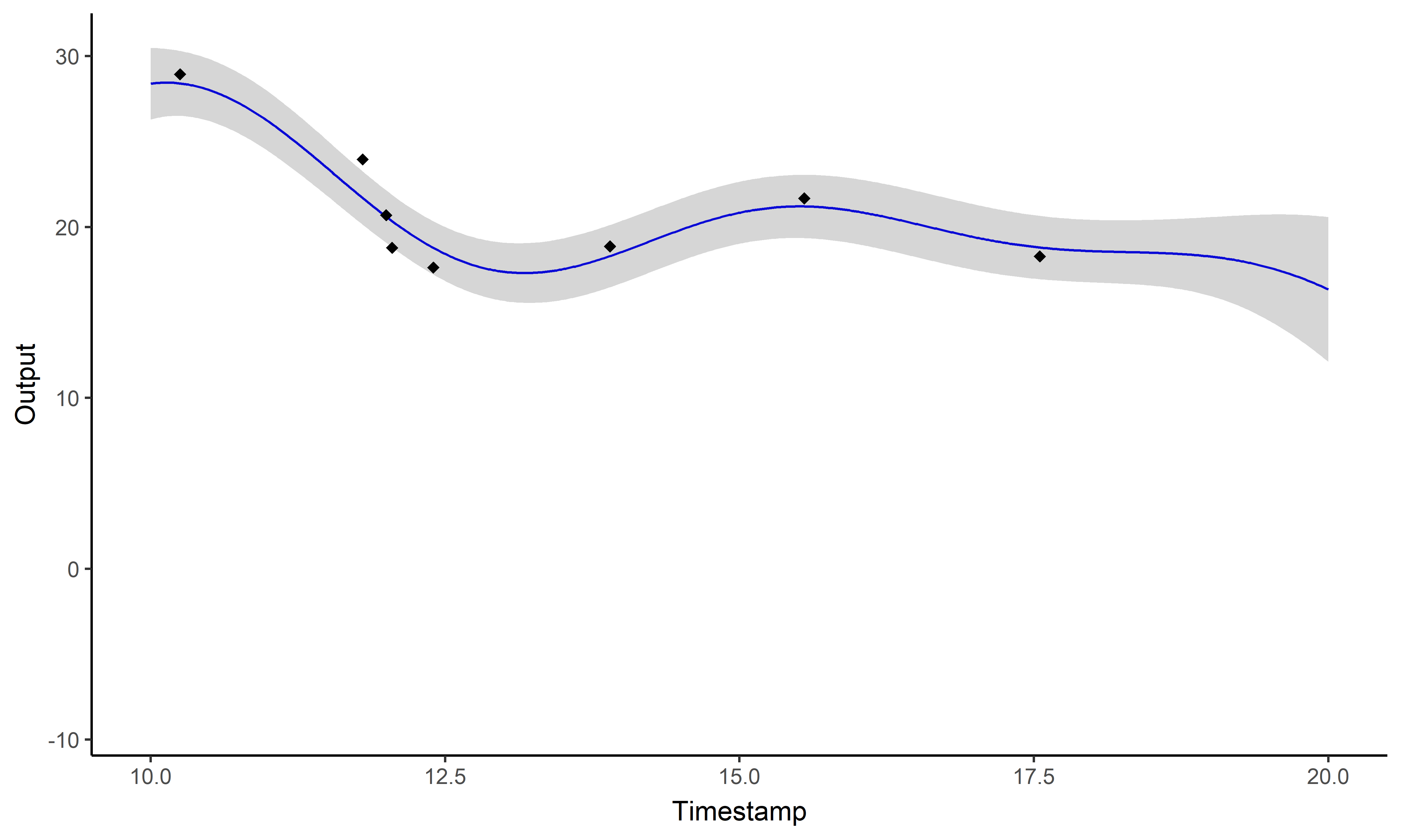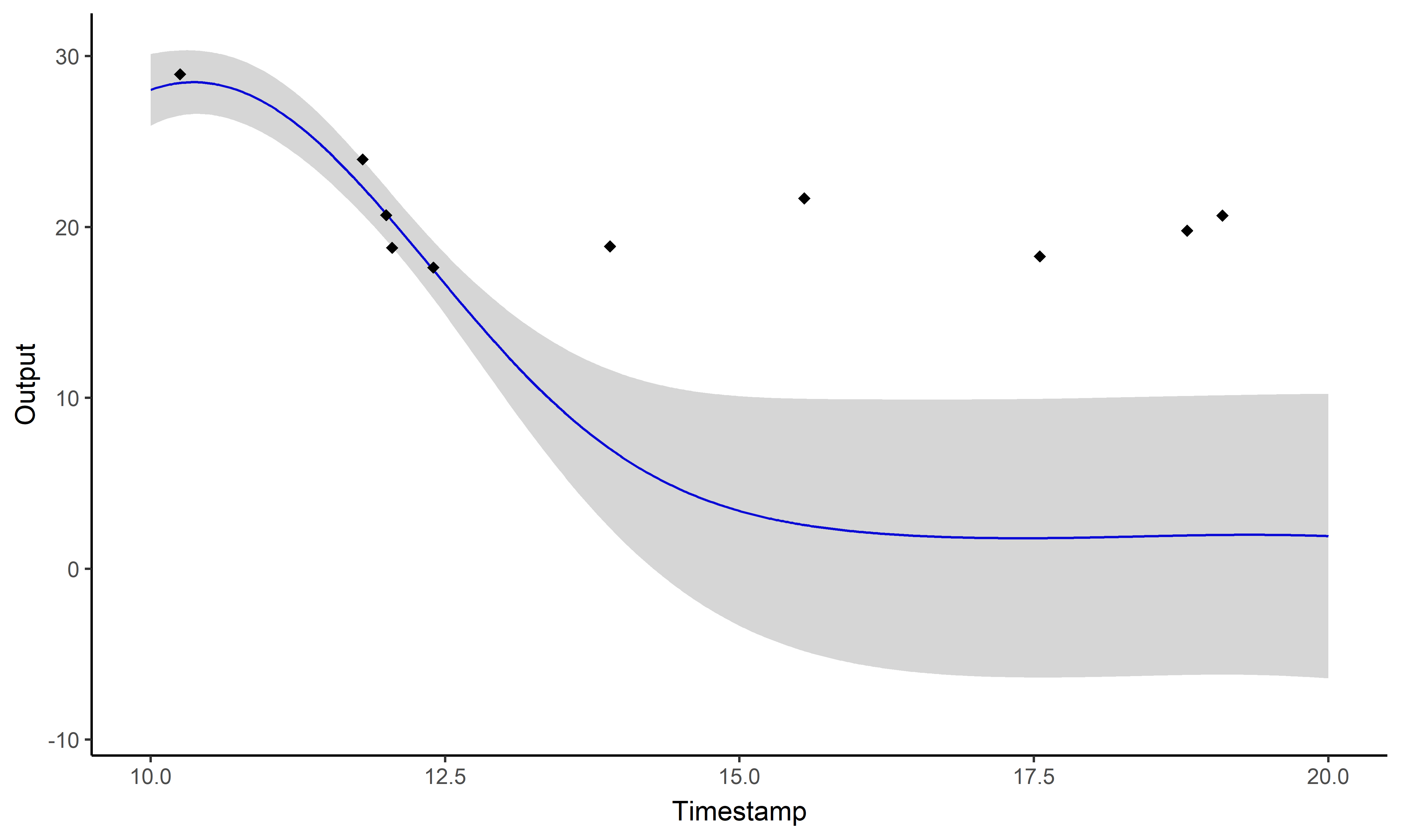
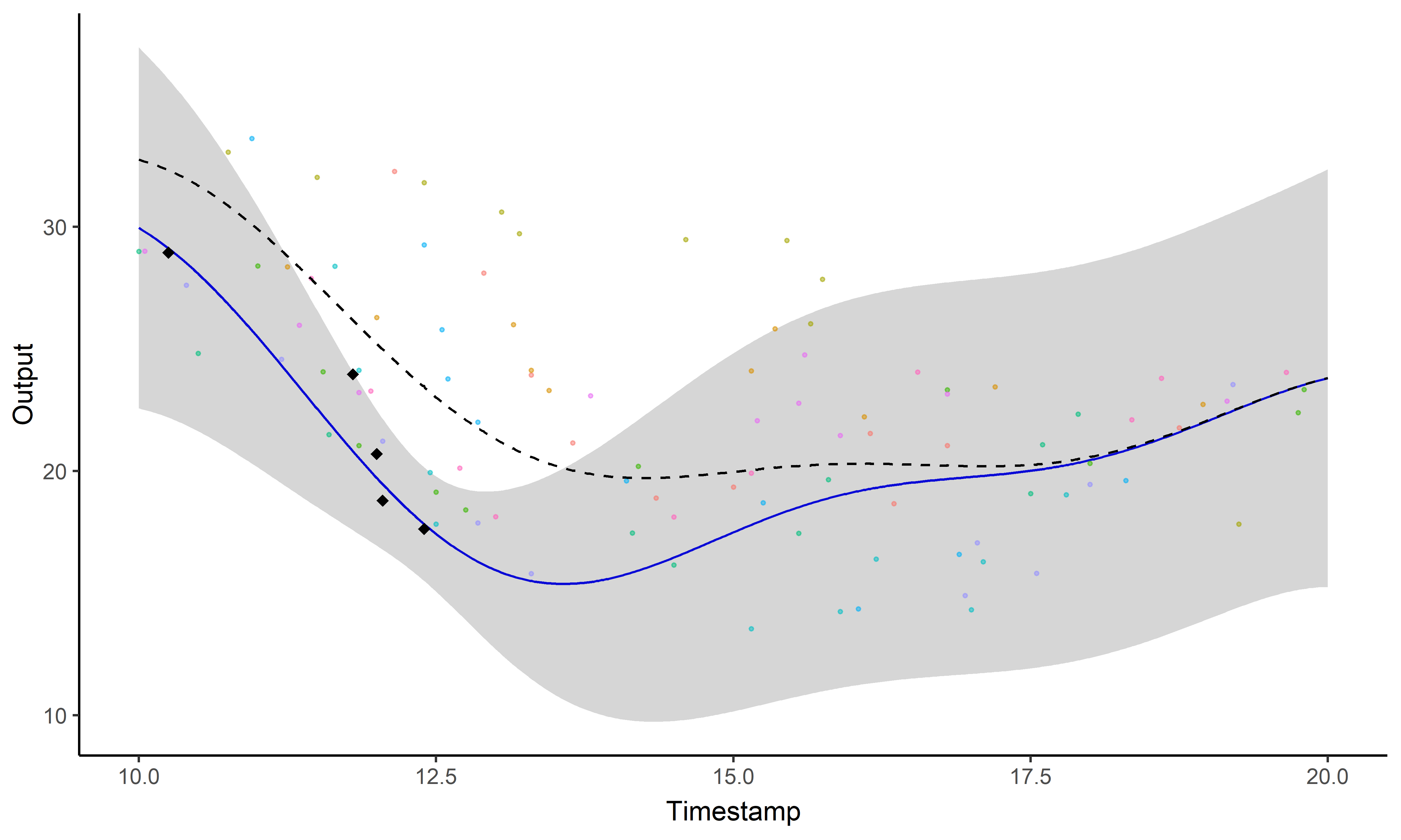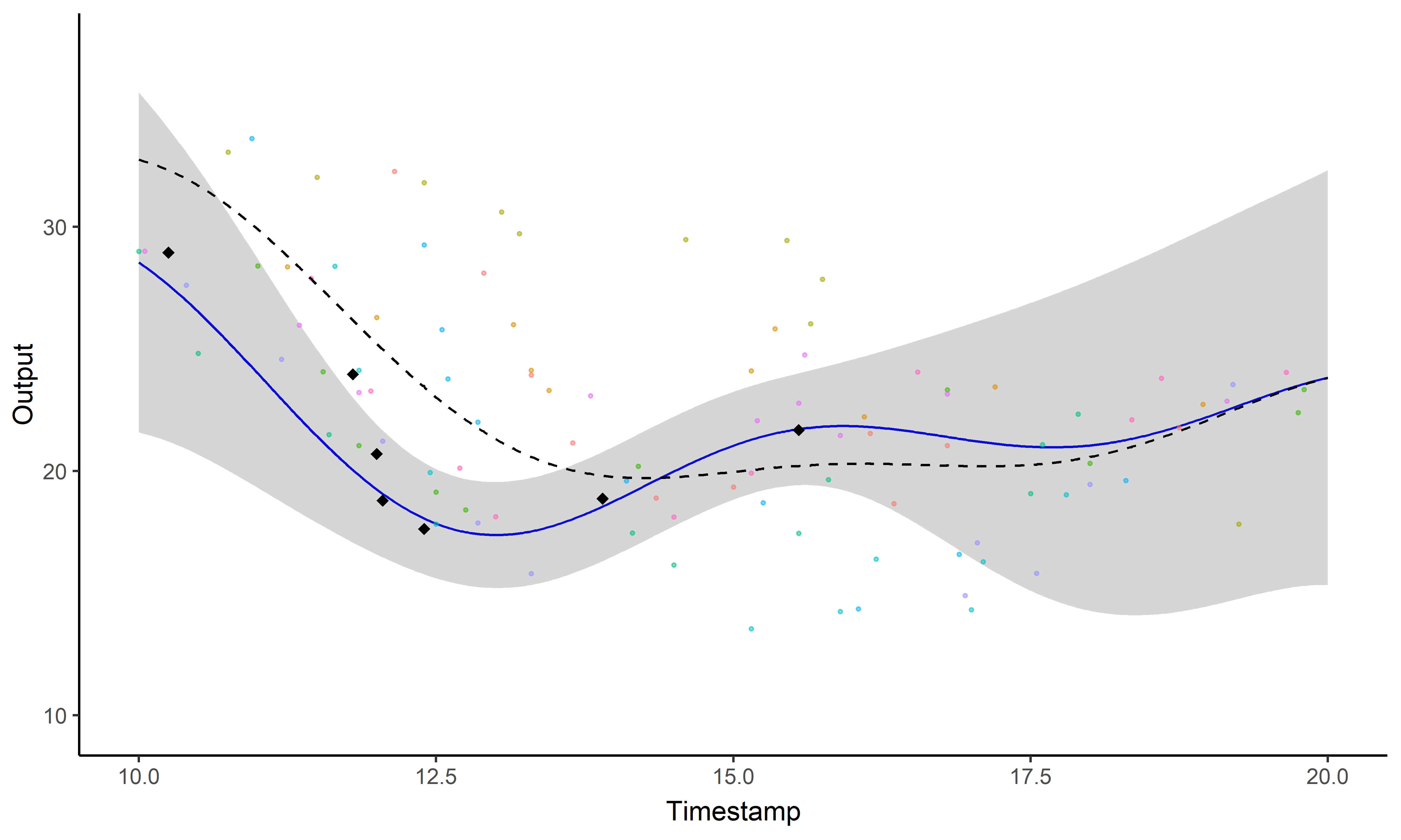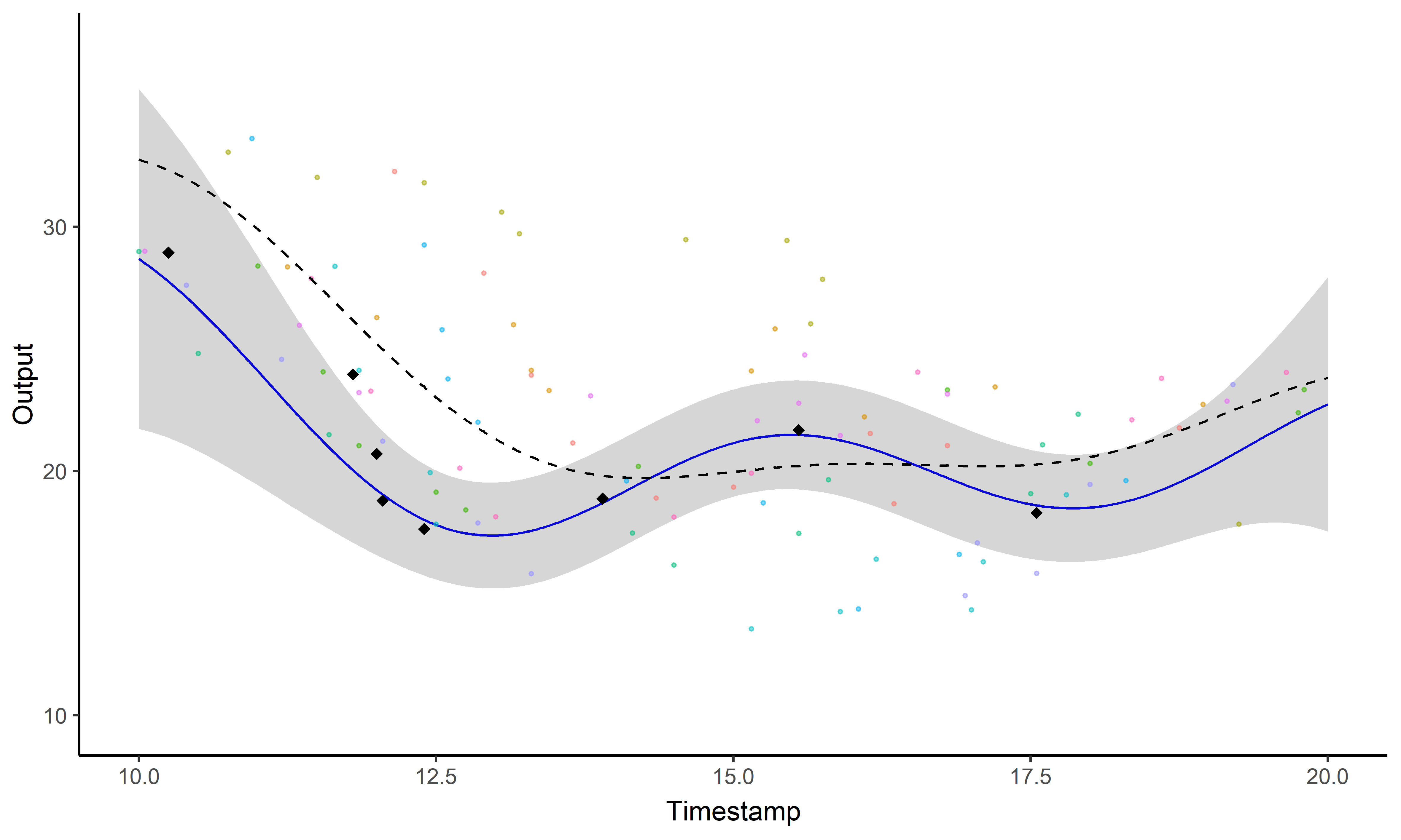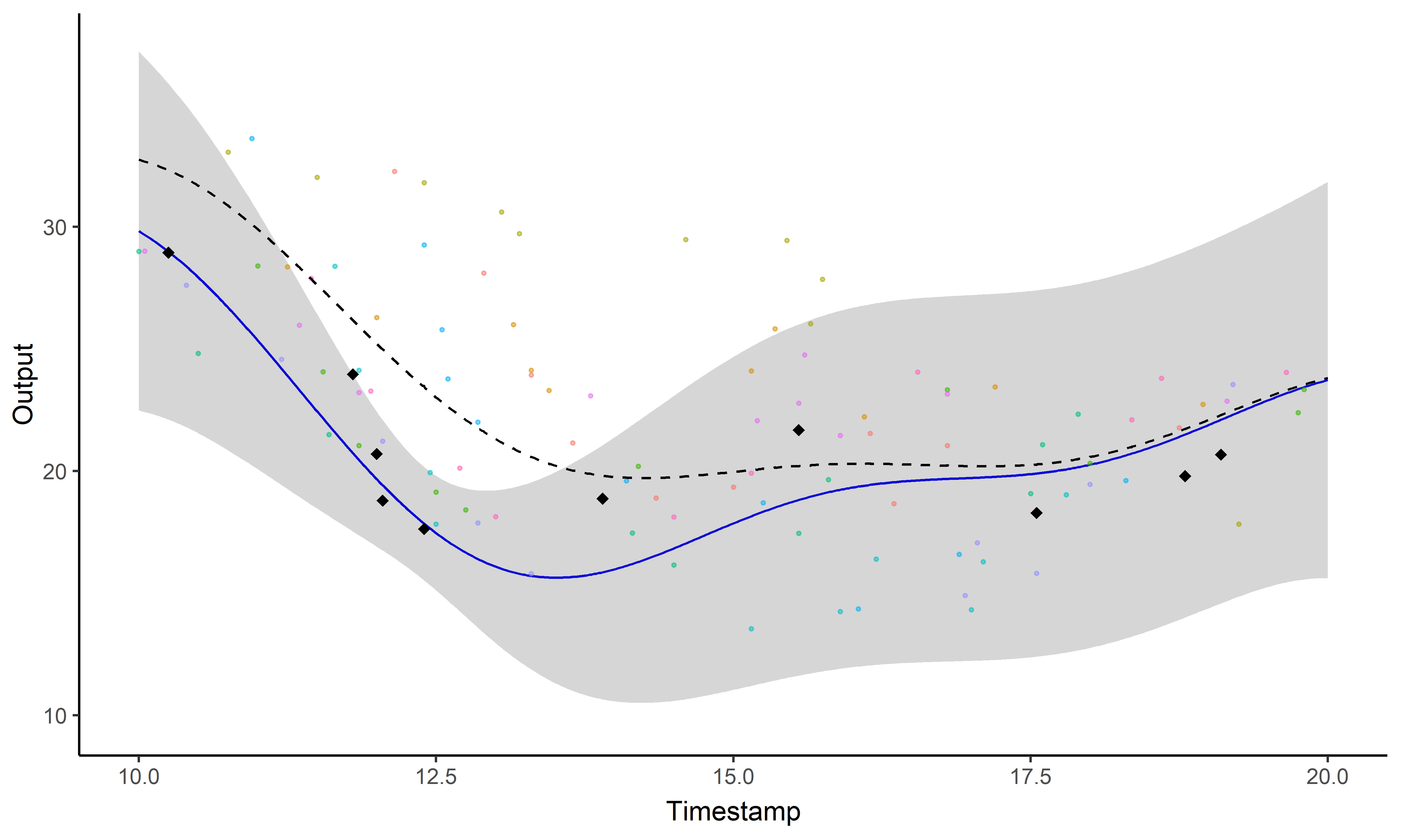
\[y_i \mid \{\color{orange}{Z_{ik}} = 1 \} = \mu_{\color{orange}{k}} + f_i + \epsilon_i\]
with: \(\ \ \ \color{orange}{Z_{i}}
\sim \mathcal{M}(1,\color{orange}{\boldsymbol{\pi}}), \ \ \
\mu_{\color{orange}{k}} \sim \mathcal{GP}(m_{\color{orange}{k}},
\color{orange}{C_{\gamma_{k}}}), \ \ \ f_i \sim \mathcal{GP}(0,
\Sigma_{\theta_i}), \ \ \ \epsilon_i \sim \mathcal{GP}(0,
\sigma_i^2).\)
\(\rightarrow\) Variational EM algorithm to learn
hyper-parameters and hyper-posterior distributions
\(\rightarrow\) Cluster-specific predictions combined into a mixture of GPs








