![image alt <]()
![image alt >]()
Multi-Means Gaussian Processes: A novel probabilistic framework for
multi-correlated longitudinal data
Arthur Leroy - Department of Computer Science, The University of Manchester
joint work with
- Mauricio Alvarez - Department of Computer Science, The University of Manchester
- Dennis Wang - Department of Computer Science, The University of Sheffield
- Ai Ling Teh - Singapore Institute for Clinical Sciences
ADSAI - Manchester - 20/06/2022
Context
Gaussian processes are elegant and well-suited tools for modelling longitudinal data. Nowadays, it is generally straightforward to:
- Fit a GP on functional or high frequency data (sparse approximations)
- Handle a few correlated time series (LMC, Multi-Output GPs, …)
However, are we able to deal with millions of correlated time series simultaneously?
For our current project, we observe:
- \(\color{blue}{M} \simeq 300\) individuals,
- with \(\color{red}{P} \simeq 700 000\) gene-related time series each,
- observed over \(N \simeq 10\) timestamps.
Context: illustration

Multi-task GP with common mean (Magma)
Leroy et al. - Magma: Inference and Prediction using Multi-Task Gaussian Processes with Common Mean - Machine Learning - 2022
\[y_i = \mu_0 + f_i + \epsilon_i\]
with:
\(\mu_0 \sim \mathcal{GP}(m_0, K_{\theta_0}),\) \(f_i \sim \mathcal{GP}(0, \Sigma_{\theta_i}),\) \(\epsilon_i \sim \mathcal{GP}(0, \sigma_i^2), \ \perp \!\!\! \perp_i.\)
It follows that:
\[y_i \mid \mu_0 \sim \mathcal{GP}(\mu_0, \Sigma_{\theta_i} + \sigma_i^2 I), \ \perp \!\!\! \perp_i\]
\(\rightarrow\) Unified GP framework with a common mean process \(\mu_0\), and individual-specific process \(f_i\),
\(\rightarrow\) Naturaly handles irregular grids of input data.
Hyper-parameters and \(\mu_0\)’s hyper-posterior are learned thanks to an EM algorithm.
A GIF is worth a thousand² words

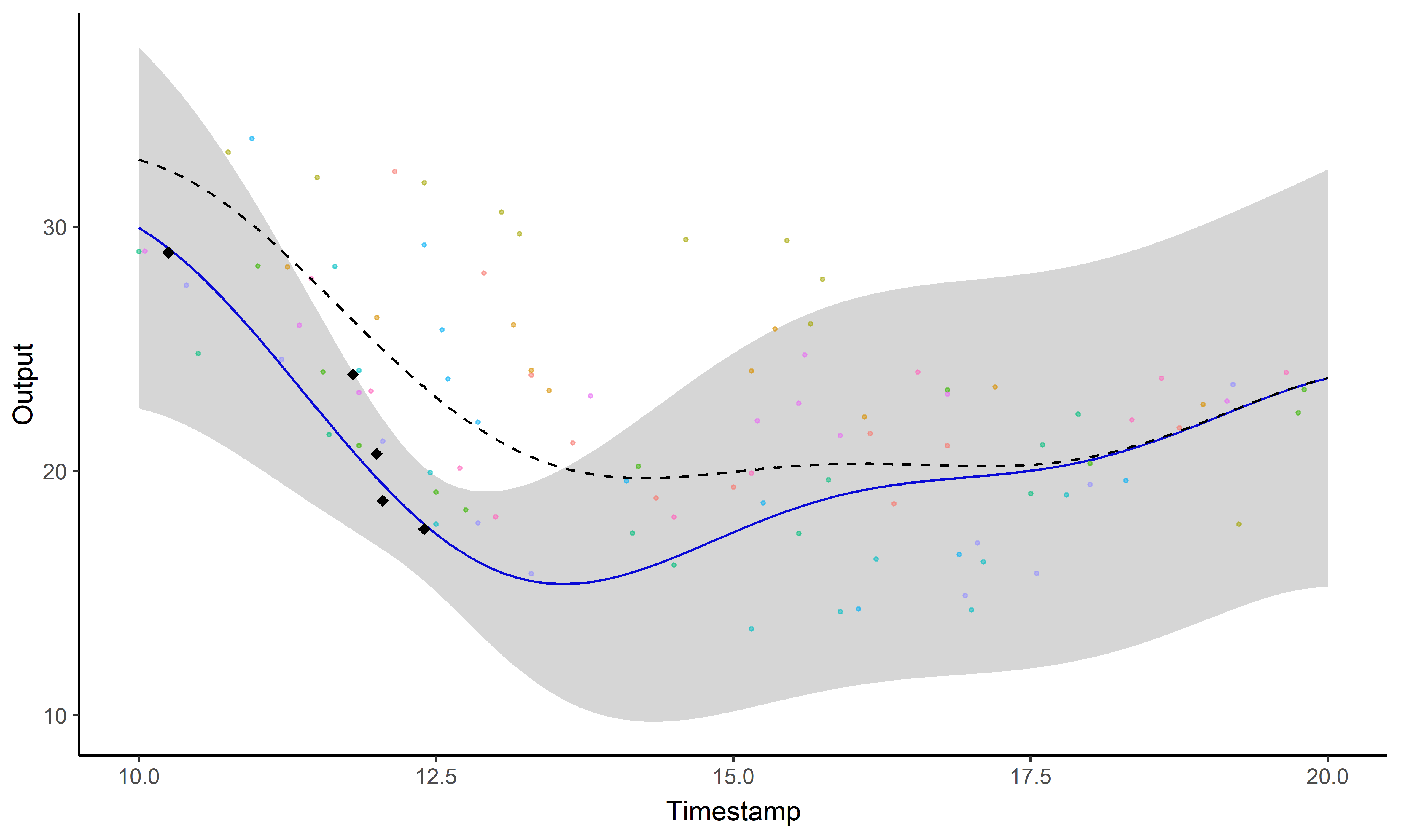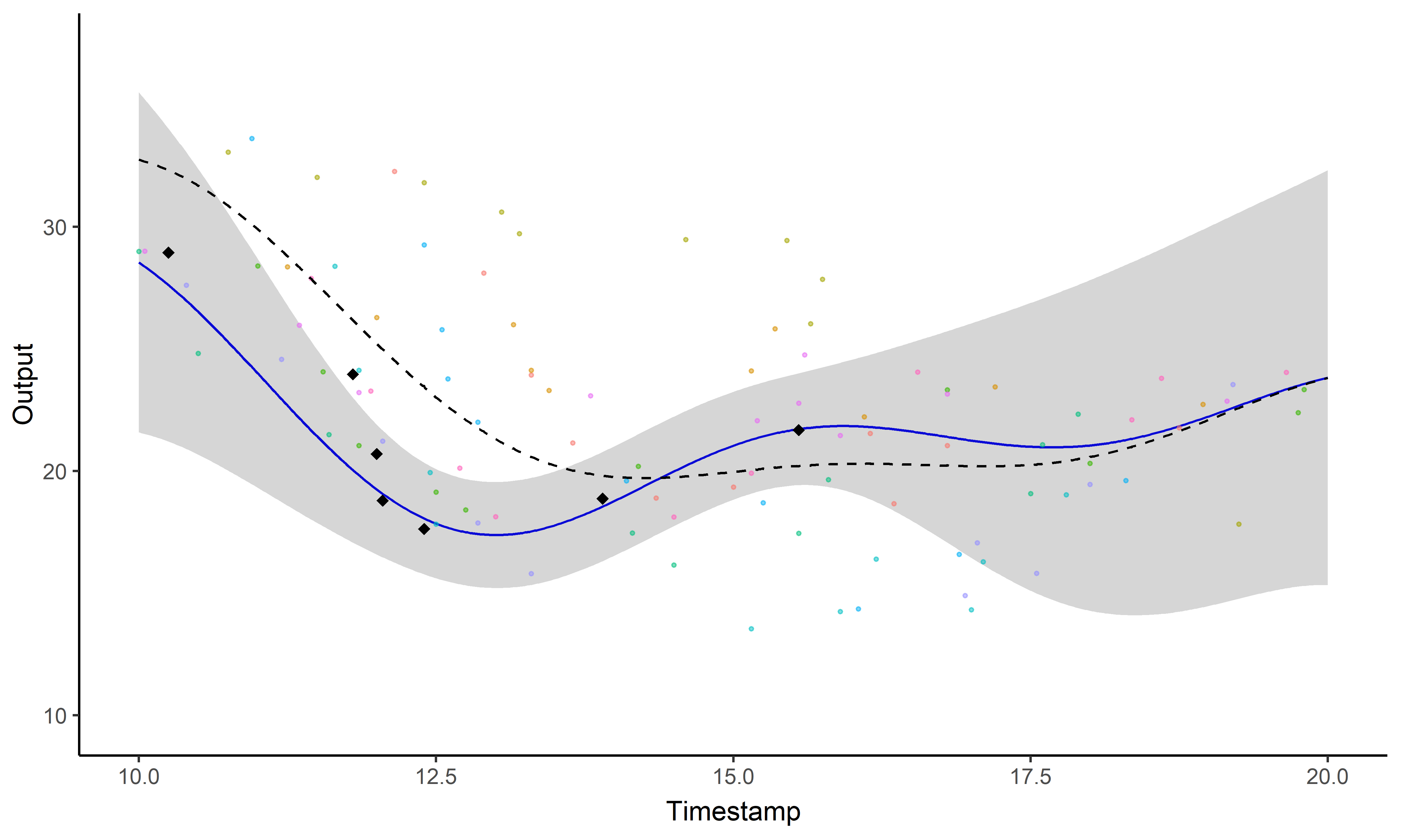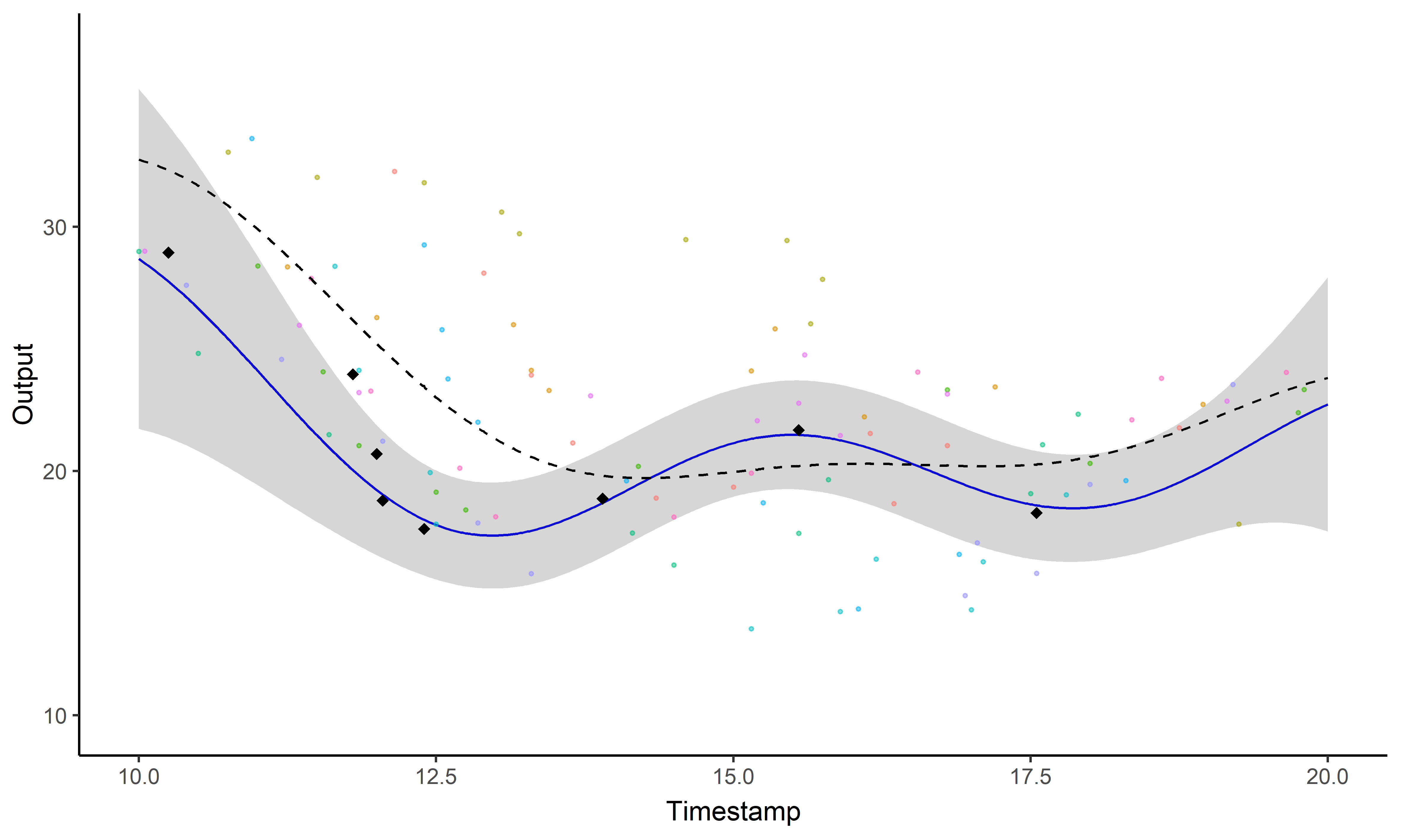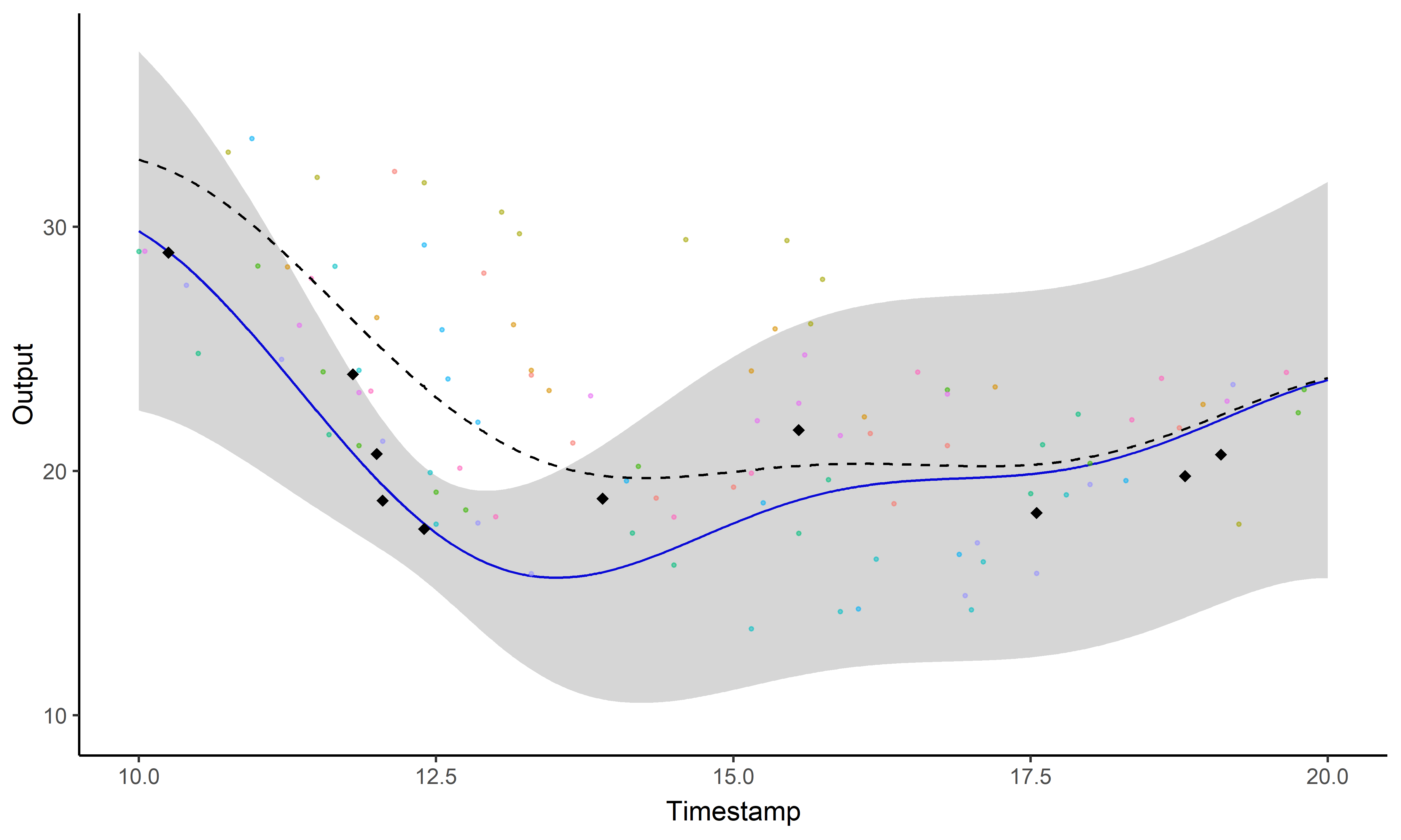
Sharing information across tasks through a common latent process to provide a well-informed mean function for prediction.
Magma + Clustering = MagmaClust
Leroy et al. - Cluster-Specific Predictions with Multi-Task Gaussian Processes - 2020
A unique underlying mean process might be too restrictive.
\(\rightarrow\) Mixture of multi-task GPs:
\[y_i \mid \{\color{green}{Z_{ik}} = 1 \} = \mu_{\color{green}{k}} + f_i + \epsilon_i\]
with:
- \(\mu_{\color{green}{k}} \sim \mathcal{GP}(m_{\color{green}{k}}, \color{green}{C_{\gamma_{k}}})\ \perp \!\!\! \perp_{\color{green}{k}}, \ \ f_i \sim \mathcal{GP}(0, \Sigma_{\theta_i}), \ \epsilon_i \sim \mathcal{GP}(0, \sigma_i^2), \ \perp \!\!\! \perp_i,\)
- \(\color{green}{Z_{i}} \sim \mathcal{M}(1, \color{green}{\boldsymbol{\pi}}), \ \perp \!\!\! \perp_i.\)
It follows that:
\[y_i \mid \{ \boldsymbol{\mu} , \color{green}{\boldsymbol{\pi}} \} \sim \sum\limits_{k=1}^K{ \color{green}{\pi_k} \ \mathcal{GP}\Big(\mu_{\color{green}{k}}, \Psi_i^\color{green}{k} \Big)}, \ \perp \!\!\! \perp_i\]
An image is still worth many words


Implemented as an R package MagmaClustR: https://github.com/ArthurLeroy/MagmaClustR
Multi-Means Gaussian processes
Different sources of correlation might exist in the data (e.g. multiple genes and individuals)
\[y_{\color{blue}{i}\color{red}{j}} = \mu_{0} + f_\color{blue}{i} + g_\color{red}{j} + \epsilon_{\color{blue}{i}\color{red}{j}}\]
with:
- \(\mu_{0} \sim \mathcal{GP}(m_{0}, {C_{\gamma_{0}}}), \ f_{\color{blue}{i}} \sim \mathcal{GP}(0, \Sigma_{\theta_{\color{blue}{i}}}), \ \epsilon_{\color{blue}{i}\color{red}{j}} \sim \mathcal{GP}(0, \sigma_{\color{blue}{i}\color{red}{j}}^2), \ \perp \!\!\! \perp_i\)
- \(g_{\color{red}{j}} \sim \mathcal{GP}(0, \Sigma_{\theta_{\color{red}{j}}})\)
Key idea for training: define \(\color{blue}{M}+\color{red}{P} + 1\) different hyper-posterior distributions for \(\mu_0\) by conditioning over the adequate sub-sample of data.
\[p(\mu_0 \mid \{y_{\color{blue}{i}\color{red}{j}} \}_{\color{blue}{i} = 1,\dots, \color{blue}{M}}) = \mathcal{N}\Big(\mu_{0}; \ \hat{m}_{\color{red}{j}}, \hat{K}_\color{red}{j} \Big), \ \forall \color{red}{j} \in 1, \dots, \color{red}{P}\]
\[p(\mu_0 \mid \{y_{\color{blue}{i}\color{red}{j}} \}_{\color{red}{j} = 1,\dots, \color{red}{P}}) = \mathcal{N}\Big(\mu_{0}; \ \hat{m}_{\color{blue}{i}}, \hat{K}_\color{blue}{i} \Big), \forall \color{blue}{i} \in 1, \dots, \color{blue}{M} \]
\[p(\mu_0 \mid \{y_{\color{blue}{i}\color{red}{j}} \}_{\color{red}{j} = 1,\dots, \color{red}{P}}^{\color{blue}{i} = 1,\dots, \color{blue}{M}}) = \mathcal{N}\Big(\mu_{0}; \ \hat{m}_{0}, \hat{K}_0 \Big).\]
Multi-Means GPs: an adaptive prediction

Multi-Means GPs: an adaptive prediction

Answer to the \(\mathbb{P}(\)first question\() \approx 1\)
\(\rightarrow\) All methods
scale linearly with the number of tasks.
\(\rightarrow\) Parallel computing
can be used to speed up training.
Overall, the computational
complexity is:
- Magma: \[ \mathcal{O}(M\times N_i^3 + N^3) \]
- MagmaClust: \[ \mathcal{O}(M\times N_i^3 + K \times N^3) \]
- Multi-Means Gaussian Processes: \[ \mathcal{O}(M \times P \times N_{ij}^3 + (M + P) \times N^3) \]
Appendix: Clustering and prediction performances


Appendix: MagmaClust, remaining clusters


