---

IA et sport :
Prédire les performances futures en natation avec des algorithmes

---

Les origines

Projet de 3 ans (2017-2020), dans le cadre d’un doctorat de mathématiques appliquées, portant sur le développement de méthodes d’apprentissage automatique pour le sport de haut-niveau.

Une problématique:

• Plusieurs études scientifiques récentes remarquent que les meilleurs jeunes sportifs atteignent rarement le haut niveau,
• Les experts du monde sportif (fédérations, entraineurs, …) demandent de nouveaux indicateurs objectifs pour aider la détection des jeunes à fort potentiel.

Une opportunité :

• La Fédération Française de Natation (FFN) propose une base de données contenant des millions de résultats issus des compétitions disputées en France depuis 2002.

Les données étudiées

Performances de membres de la FFN, au cours de leur carrière, sur 100m nage libre :

Les données étudiées

Performances de membres de la FFN, au cours de leur carrière, sur 100m nage libre :

• Données temporelles irrégulières (nombre de points et temps d’observations différents),
• Beaucoup de nageurs pour chaque épreuve,

Les données étudiées

Performances de membres de la FFN, au cours de leur carrière, sur 100m nage libre :

• Données temporelles irrégulières (nombre de points et temps d’observations différents),
• Beaucoup de nageurs pour chaque épreuve,
• Peu d’observations pour chaque nageur.

Un problème, trois questions

Existe-t-il des profils de progressions spécifiques parmi les nageurs ?

Leroy et al. - Functional Data Analysis in Sport Science: Example of Swimmers’ Progression Curves Clustering - Applied Sciences - 2018

Est-il possible de prédire des performances futures (et quantifier nos certitudes) ?

Leroy et al. - Magma: Inference and Prediction with Multi-Task Gaussian Processes - Under submission in Statistics and Computing - 2020 - https://github.com/ArthurLeroy/MAGMA

Est-ce-que former des groupes d’individus permet d’améliorer les prédictions ?

Leroy et al. - Cluster-Specific Predictions with Multi-Task Gaussian Processes - Under submission in JMLR - 2020 - https://github.com/ArthurLeroy/MAGMAclust

Un problème, trois questions

Existe-t-il des profils de progressions spécifiques parmi les nageurs?

Travailler avec des fonctions et faire des groupes

Pour pouvoir comparer les individus il est nécessaire de définir une représentation commune, et de reconstruire des données fonctionnelles à partir des points d’observations.

L’utilisation d’algorithmes de clustering de courbes permet d’identifier différents profils de progression, correspondant bien à ce qui est observé par les experts de la natation en pratique.

Limites des algorithmes existants

• Modélisation individuel insatisfaisante,
• Pas de prise en compte de l’incertitude,
• Difficulté de traitement des temps d’observation irréguliers.

Une question bonus

Mais au fait, comment fait on pour apprendre ?

Quelques clarifications sur les termes à la mode

Le travail présenté ici se concentre sur deux grands problèmes de machine learning :

• L’apprentissage supervisé, où l’on cherche à généraliser à partir de données du type entrée-sortie pour faire des prédictions.
• L’apprentissage non-supervisé (ou clustering), où l’on cherche les structures de groupe dans des données de même type.

Apprentissage supervisé, les grands principes

où :

Tout le problème de l’apprentissage supervisé consiste à trouver la bonne fonction \(\color{green}{f}\), en s’aidant de données observées \(\{(x_1, y_1), \dots, (x_n, y_n) \}\), pour pouvoir effectuer des prédictions lorsque l’on observe une nouvelle donnée \(x_{n+1}\).

Apprentissage supervisé 1.0, le regréssion linéaire

L’exemple le plus simple est celui de la régression linéaire, où l’on fait l’hypothèse que :

Trouver la meilleure fonction \(\color{green}{f}\) revient à estimer la bonne valeur de \(a\) et \(b\) pour nos données.

La formule de Bayes

Cette simple formule a de grandes implications sur la façon d’apprendre à partir de données.

avec :

• \(\mathbb{P}(\color{red}{T})\), la probabilité que la théorie \(\color{red}{T}\) soit vraie, ce que l’on pense a priori.
• \(\mathbb{P}(D \mid \color{red}{T})\), la probabilité d’obtenir ces données si la théorie \(\color{red}{T}\) est vraie, la vraisemblance.
• \(\mathbb{P}(D)\), la probabilité d’obtenir ces données, une constante de normalisation.

La formule de Bayes indique comment mettre à jour ce que l’on pense de \(\color{red}{T}\) en tenant compte des données D :

• \(\mathbb{P}(\color{red}{T} \mid D)\), la probabilité que la théorie \(\color{red}{T}\) soit vraie au vu des données, ce qu’il faut penser a posteriori.

Mais comment on apprend à bien apprendre ?

Illustrons ce résultat avec un exemple classique. Si il existe une maladie telle que :

• \(\mathbb{P}(\color{red}{M}) = 0.001\), 1 personne sur 1000 est malade en moyenne,
• \(\mathbb{P}(D \mid \color{red}{M}) = 0.99\), un test de dépistage est fiable à 99% si vous êtes malade,
• \(\mathbb{P}(\bar{D} \mid \bar{\color{red}{M}}) = 0.99\), ce même test de dépistage est fiable à 99% si vous n’êtes malade,

Alors, si vous avez un résultat positif au test, la formule de Bayes vous informe que vous avez en réalité une probabilité d’être malade égale à :

Ainsi, on aurait seulement 9% de chance environ d’être effectivement malade malgré un résultat positif au test.

Apprendre une fonction grâce à Bayes ?

Bien que la formule de Bayes soit connue depuis longtemps, il est général très difficile de calculer certains termes.

Cependant, les récents développements de l’informatique et les grandes puissances de calcul ont permis de le développement de la statistique Bayésienne, qui au coeur de nombreux algorithmes d’apprentissage.

Cette approche permet de raisonner en terme de probabilités, et de quantifier l’incertitude de nos prédictions.

En particulier, un algorithme très populaire pour apprendre notre fonction d’apprentissage \(\color{green}{f}\) et effectuer des prédictions probabilistes repose sur l’utilisation des processus gaussiens.

Processus gaussien, ou le miracle de l’apprentissage probabiliste

Pas de restrictions sur \(\color{green}{f}\) mais des probabilités a priori parmi toutes les fonctions possibles.

Prédiction à l’aide d’un processus gaussien

Les processus gaussiens offrent un cadre de modélisation idéal mais restent insuffisants pour faire des prédictions (surtout à long terme).

Un problème, trois questions

Est-il possible de prédire des performances futures (et quantifier nos certitudes) ?

Parfois le problème concret inspire l’innovation mathématique

Partant du constat que tous les nageurs partagent de nombreuses caractéristiques communes, pourquoi ne pas introduire un processus gaussien \(\mu_0\), commun à tous les individus ?

avec :

Cette équation est appelé le modèle génératif de nos données. On fait l’hypothèse que les données réelles sont issues d’un phénomène qui fonctionne selon cette formule.

Une telle approche, de partage d’information entre plusieurs individus, est généralement appelée apprentissage multi-tâches.

Multi-tAsk GP with coMmon meAn (Magma)

Un nouvel algorithme, appelé Magma, est développé pour apprendre les valeurs probables de \(\mu_0\) sachant nos données, en utilisant la formule de Bayes :

Ainsi, tous les individus déjà observés vont servir à estimer la loi de probabilité du processus commun \(\mu_0\).

Utiliser \(\mu_0\) dans la prédiction : l’idée clef

Une fois que l’on a appris \(\mu_0\), il est très difficile de savoir comment utiliser les informations qu’il contient. Même si cette étape aura été (de loin) la plus longue à accomplir, la solution à ce problème s’écrit finalement en quelques lignes. Il faut pour cela :

• considérer que l’on connait (conditionnement) toutes les données d’entrainement à chaque fois que l’on veut effectuer des prédictions pour un nouvel individu,
• faire transiter l’information par \(\mu_0\) (intégration).

Des formules et du code

Quelques étapes supplémentaires seront nécessaires pour achever notre algorithme :

• Définir les formules de prédiction pour les temps non-observés,
• Résoudre le problème des observations à temps irréguliers,
• Implémenter les équations (\(\simeq 2000\) lignes de code).

Une image vaut 1000 mots

• Mêmes données, mêmes paramètres
• Processus gaussien strandard (gauche), Magma (droite)

Un GIF vaut \(10^9\) mots

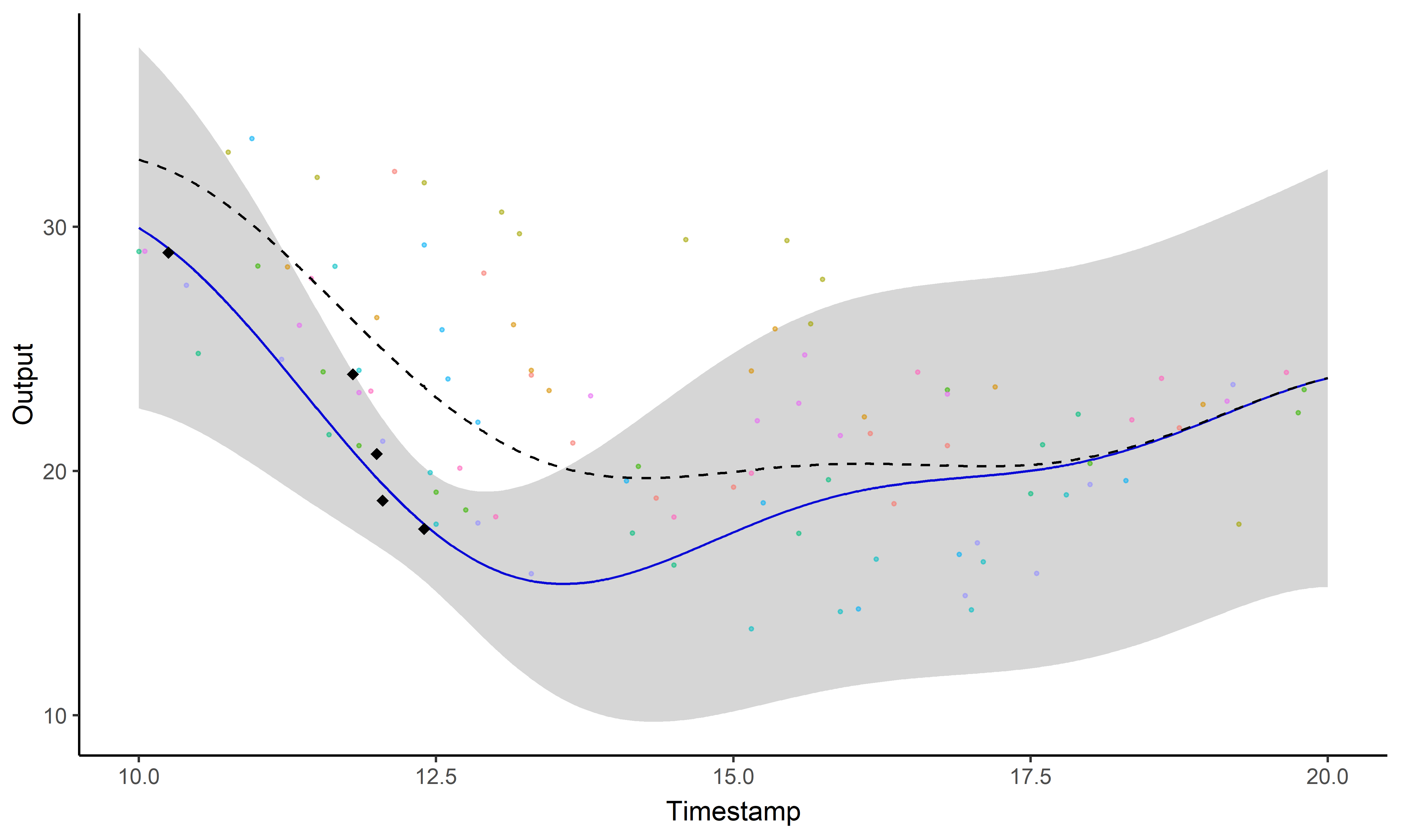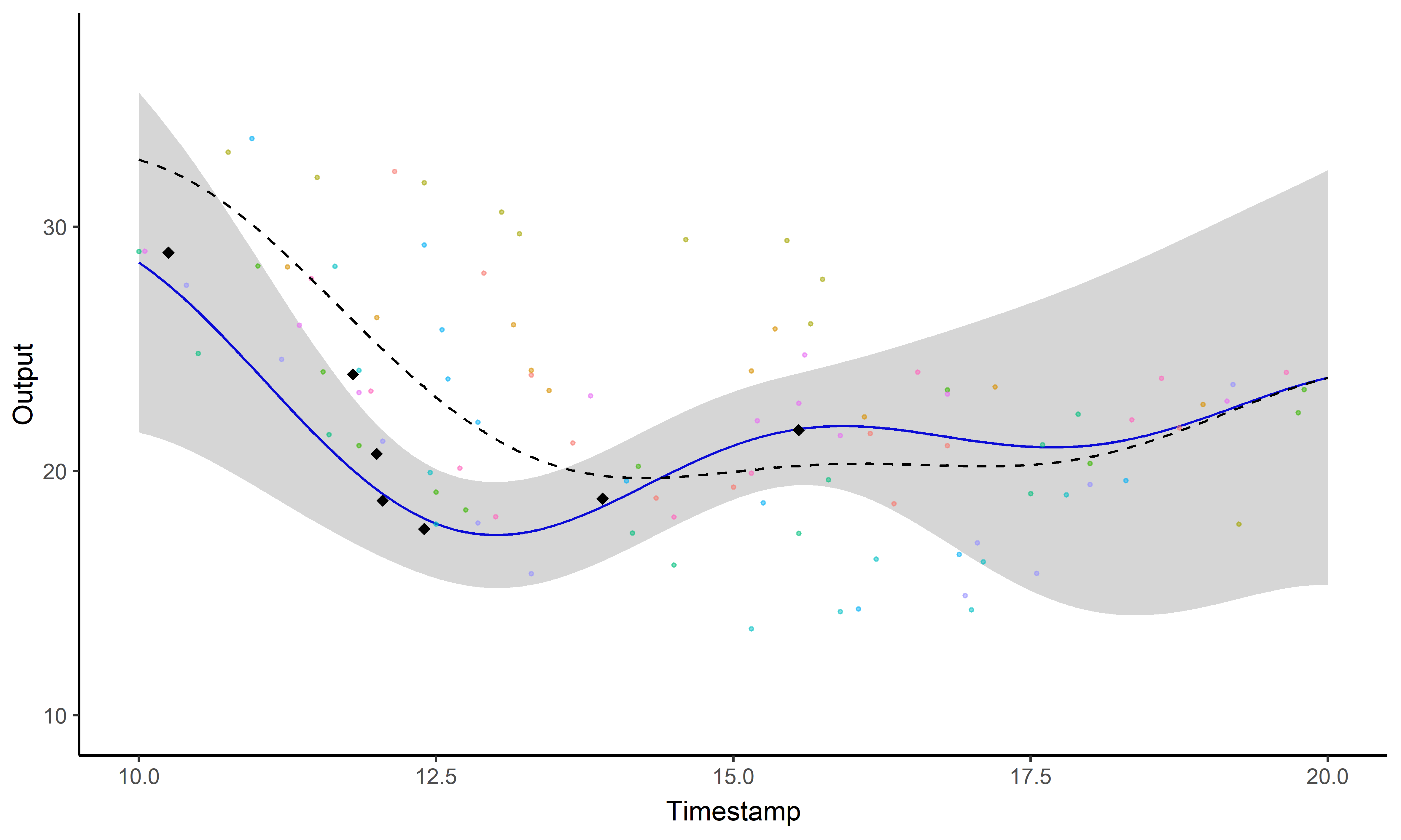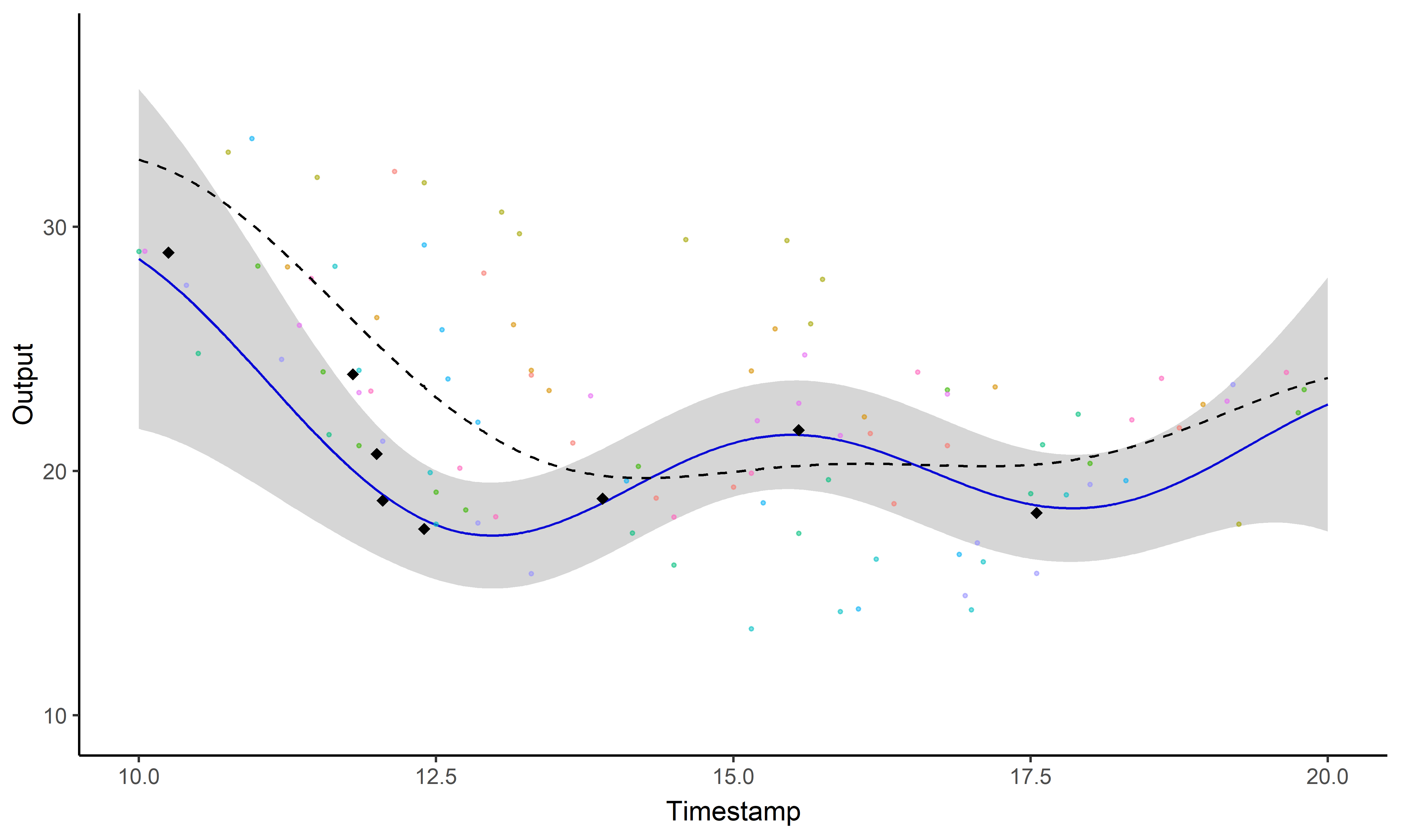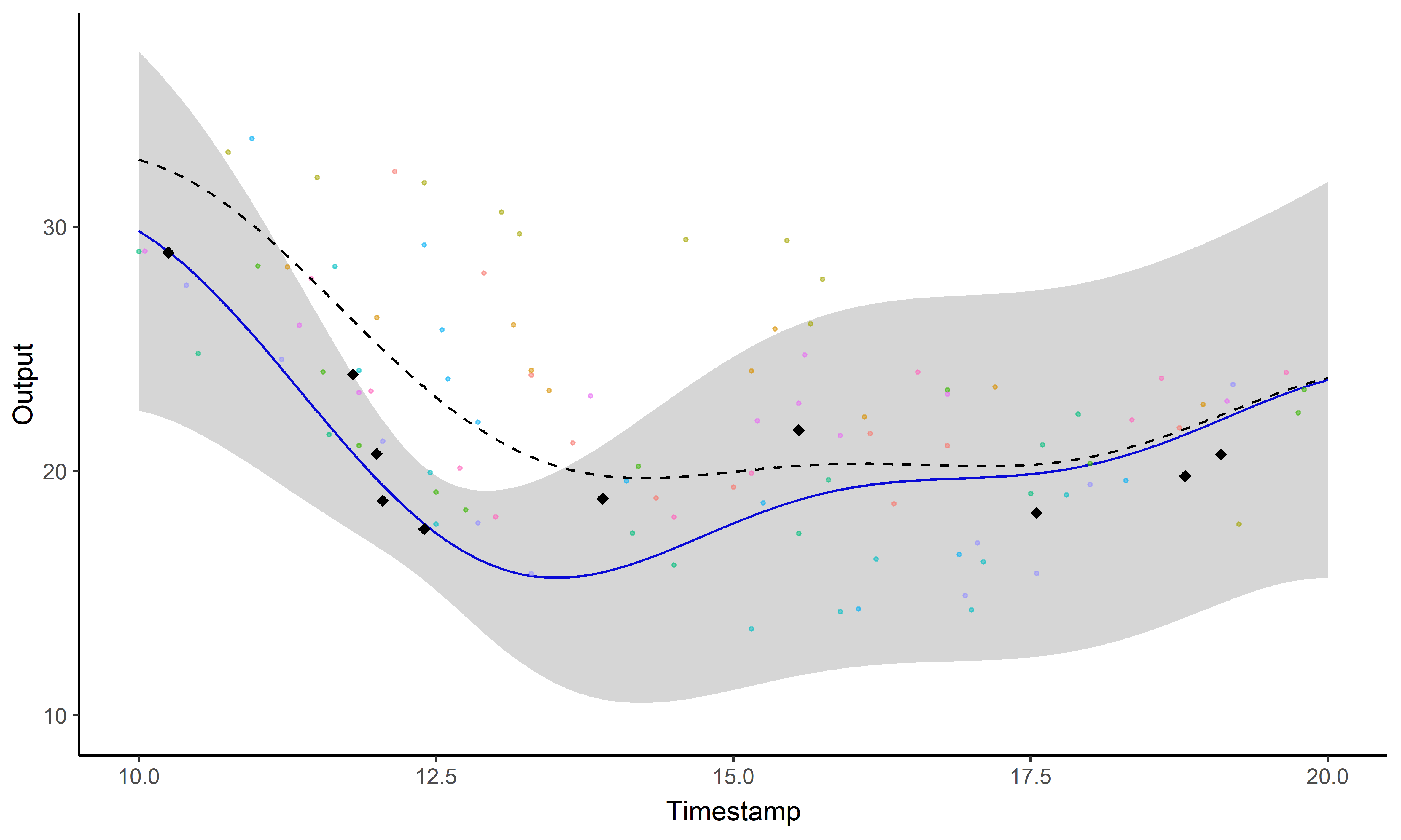
Un problème, trois questions

Est ce que former des groupes d’individus permet d’améliorer les prédictions?

Magma + Clustering = MagmaClust

Encore une fois, la problèmatique sportive nous offre une perspective d’amélioration du modèle.

En identifiant différents groupes, le partage d’information pourrait être plus pertinent entre les individus qui se ressemblent.

On peut ainsi definir une procédure de clustering au sein de notre algorithme, simplement en définissant un processus \(\mu_k\) spécifique pour chaque groupe.

Et il est toujours possible d’apprendre tous les \(\mu_k\), mais aussi les probabilités d’appartenance à chacun des groupes, pour tous les individus.

Le duel final : Magma vs MagmaClust

Une prédiction qui dépend du groupe d’appartenance

L’apprentissage des processus moyens en image

Qualité de prédiction sur données simulées

La complexité algorithmique

Un aspect important de tout algorithme, notamment pour l’apprentissage automatique, réside dans sa complexité algorithmique

Cette mesure nous indique dans quel ordre de grandeur le nombre d’opérations (et donc le temps de calcul) augmente en fonction de la dimension des données d’entrées du modèle. Dans notre cas de figure, nous avons :

• Magma: \[ \mathcal{O}(M\times N_i^3 + N^3) \]
• MagmaClust: \[ \mathcal{O}(M\times N_i^3 + K \times N^3) \]

avec :

• \(M\), le nombre d’individus,
• \(N_i\), le nombre de temps d’observations de l’individus \(i\),
• \(N\), le nombre de points d’observations différents totaux,
• \(K\), le nombre de clusters.

Et nos nageurs dans tout ça ?

Et nos nageurs dans tout ça ?

Et nos nageurs dans tout ça ?

Qualité de prédiction pour tous les nageurs

Ai-je précisé que j’aimais les GIFs ?

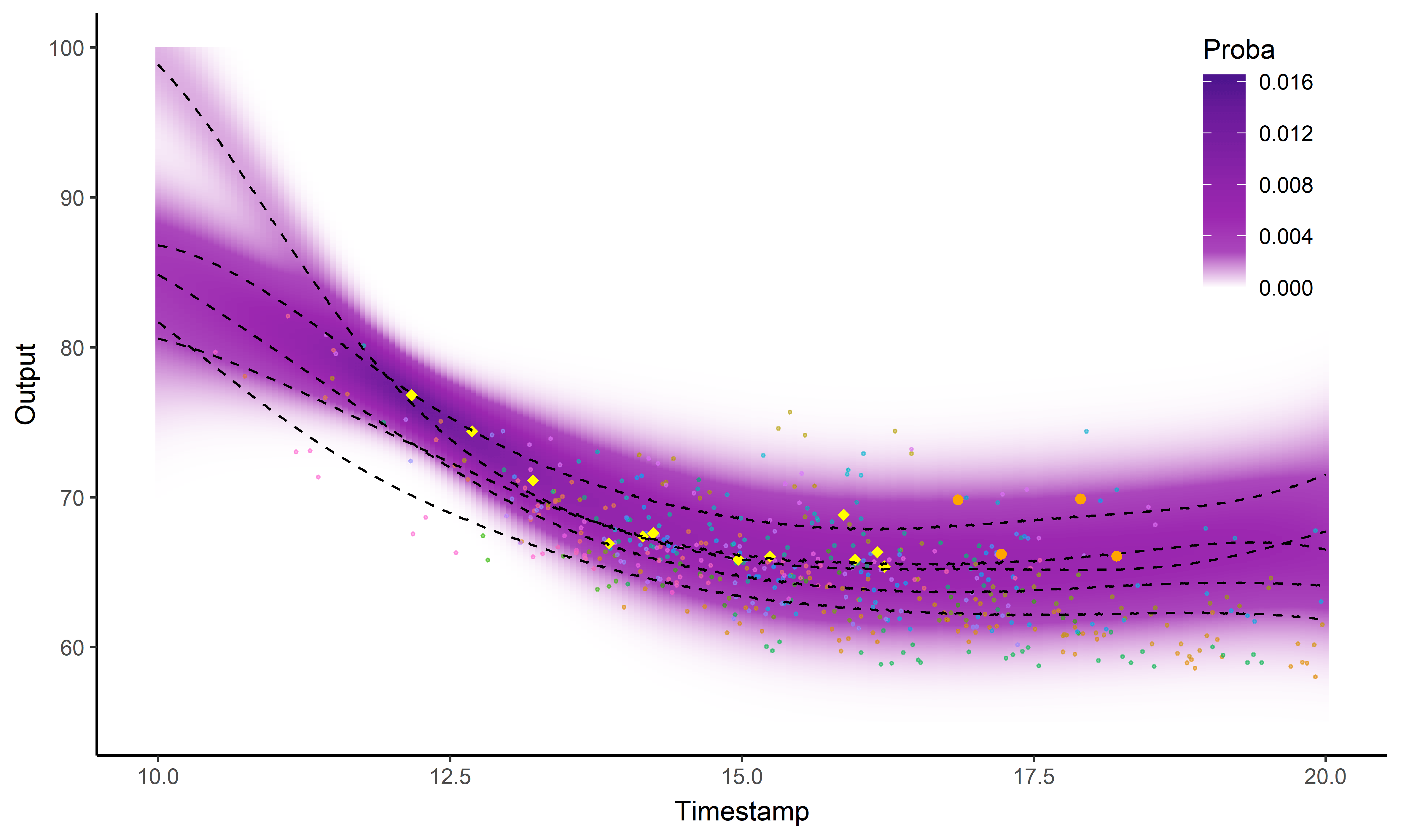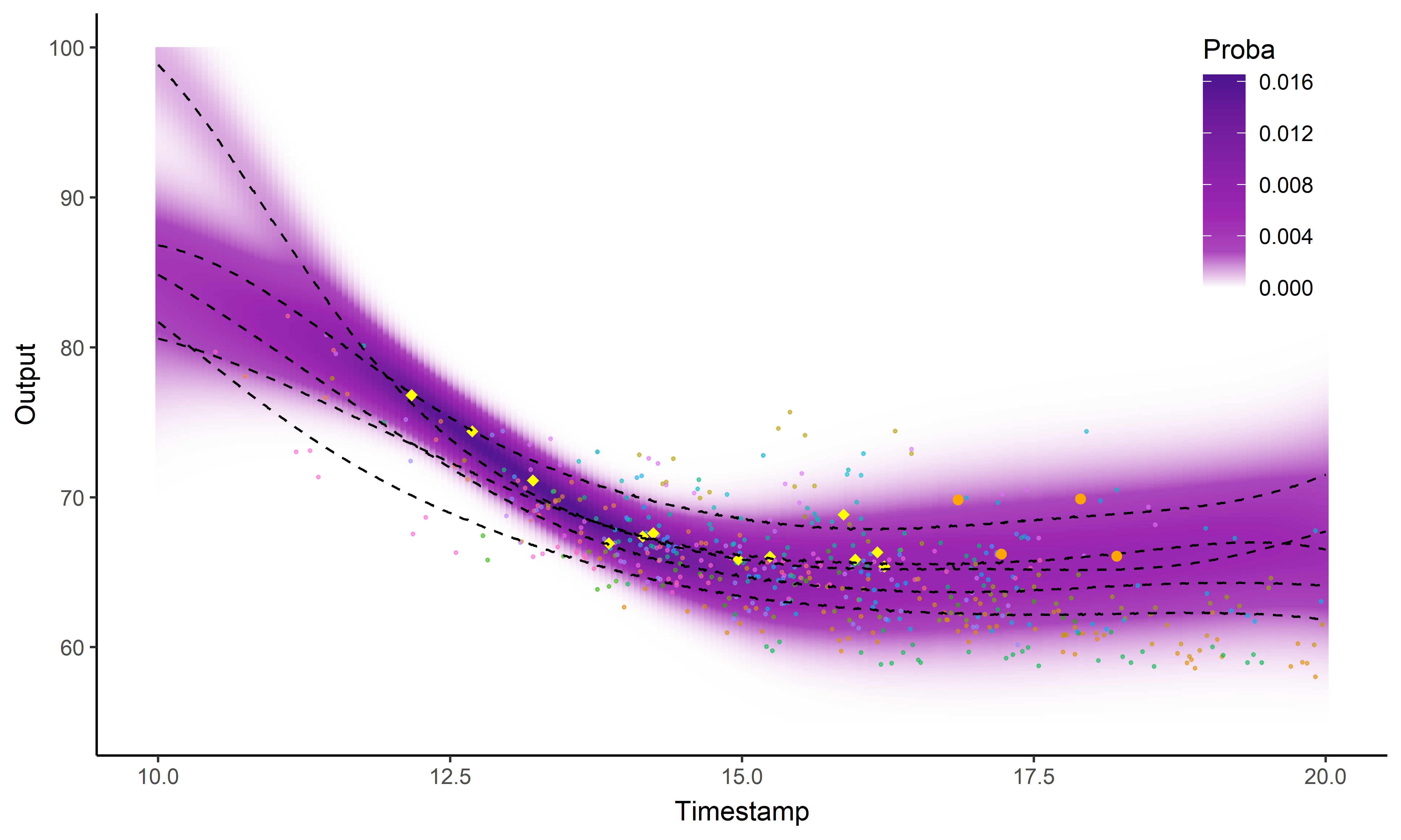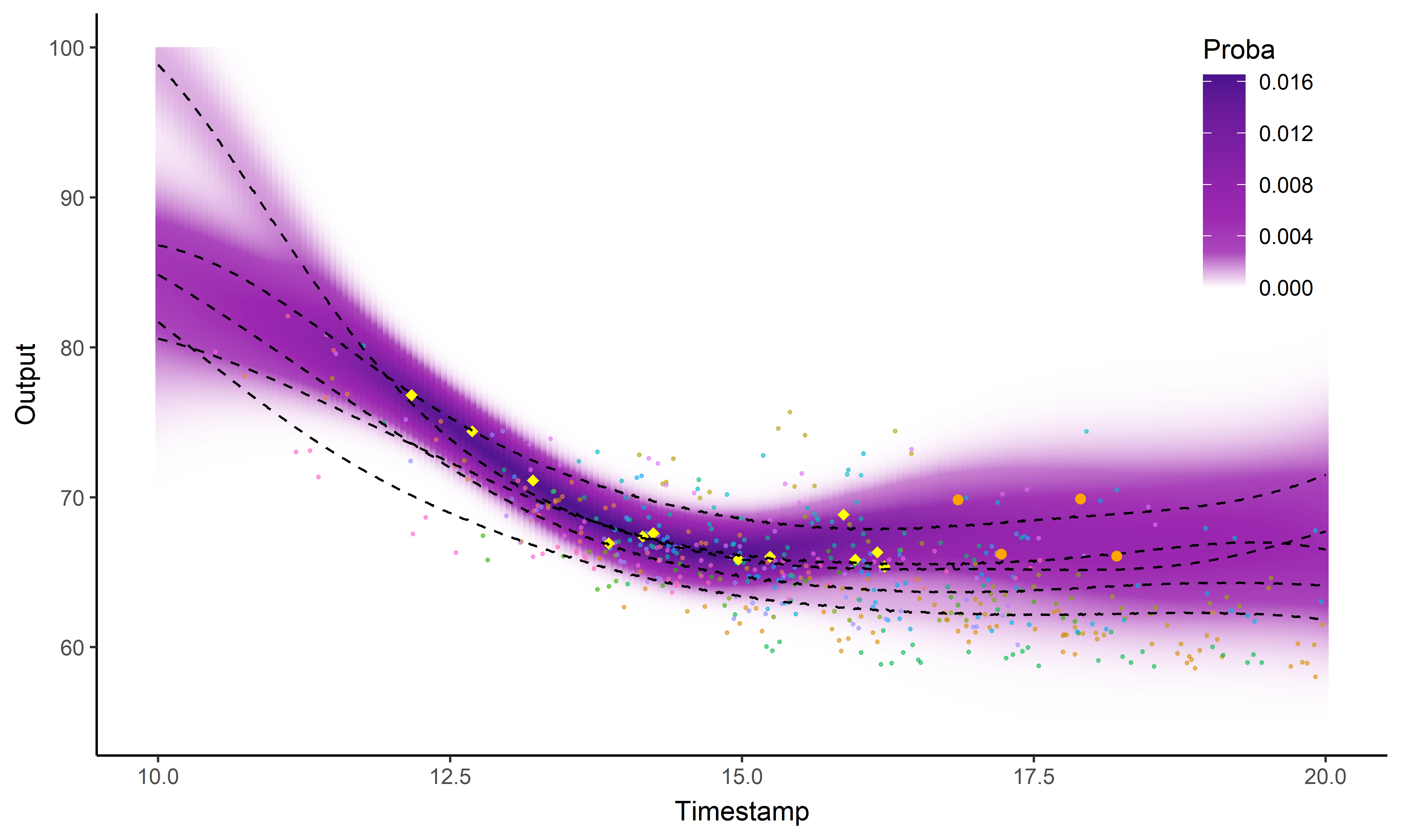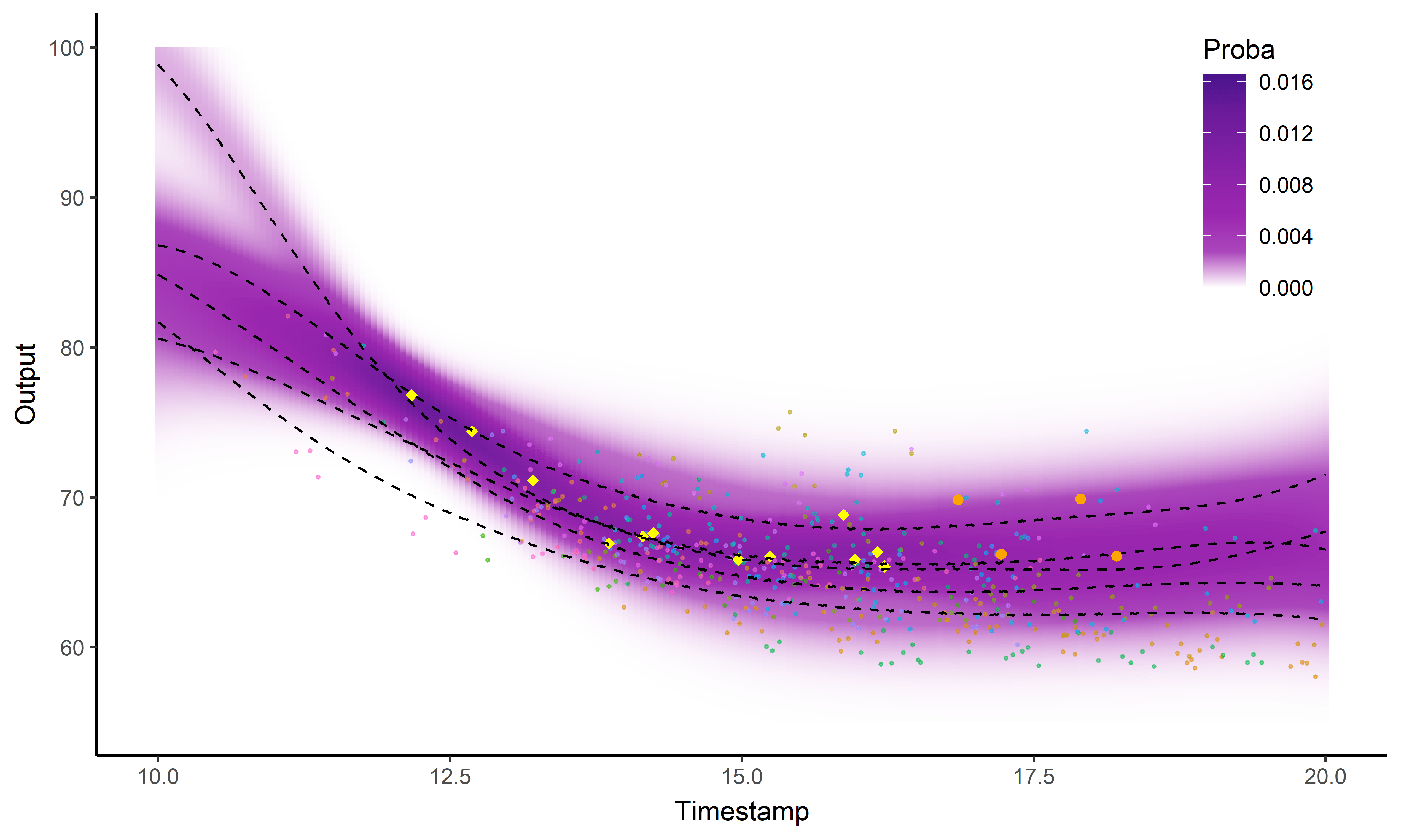
Intégration dans une application web FFN

Intégration dans une application web FFN

Projets à venir

• Amélioration des modèles et recherche théorique,
• Optimisation du code et implémentation de librairies R et Python,
• Intégration à l’appli web FFN,
• Tests grandeur nature avec de jeunes nageurs ?

Un GIF de chat, ça n’a pas de prix